帽檐斜切式洞门斜率对隧道气动性能的影响

张雷，田红旗，杨明智，张健，曾祥坤，杨志刚

(1.中南大学 交通运输工程学院，轨道交通安全教育部重点实验室，湖南 长沙，410075；2.中国铁道科学研究院 信息研究所，北京，100086)

我国高铁线路长，隧道多，运营车速高，列车高速通过隧道可引起车体表面和隧道壁面剧烈的瞬变压力变化，其对列车安全运行、旅客乘坐舒适性的不良影响进一步加重[1-2]；当列车高速进入隧道时，列车前方的空气突然受到压缩，形成压缩波，压缩波以音速传到隧道出口，向外膨胀形成微气压波，严重时会产生爆破音，对洞口周围环境及居民的正常生活造成一定的影响[3-4]：因此，如何改善高铁隧道气动性能，是铁路隧道设计中必须解决的关键技术问题。世界各国多以优化列车外形或减速进入隧道的方式达到控制车体表面和隧道壁面瞬变压力变化的目的[5-6]，并在隧道入口处设置不同形式的隧道洞门与缓冲结构以减小隧道出口微气压波的影响[7-9]。我国高速铁路隧道的设计中广泛应用新型的帽檐斜切式隧道洞门结构，目前国内外在缓冲结构对隧道空气动力效应的影响方面进行了大量的研究，并获得一系列的研究成果，但是，由于帽檐斜切式隧道洞门是一种新型隧道洞门，且已应用于京沪和武广等多条新建或在建高速铁路，其对隧道空气动力效应的影响也亟待深入研究[10-11]。为此，本文作者采用三维数值模拟计算，对不同斜切斜率时，帽檐斜切式洞门下的隧道空气动力效应问题进行研究，并用动模型试验对研究结果进行验证。

1 数值计算与动模型试验

1.1 数值计算

采用 FLUENT流场计算软件进行三维数值模拟计算，通过结构和非结构网格相结合的混合网格分别对计算区域和车体表面进行离散，采用有限体积法和相关流动控制方程真实模拟列车周围流场。描述列车周围空气流动的控制方程包括连续性方程、动量方程、能量方程、气体状态方程及湍流模型方程，FLUENT提供了多种湍流模型[12-13]。本文选取工程上应用较广的k-ε双方程模型，按三维、可压缩、非定常N-S方程，采用滑移网格技术，对高速列车通过隧道时复杂的空气流场进行模拟计算。

数值计算采用1∶1的比例模型，高速列车由头车和尾车两车编组而成，其头部流线型长度为6.18 m，车速为350 km/h。在车体靠近隧道壁面一侧布置2个数据监控点(以下简称测点)，如图 1所示；双线隧道净空面积100 m2，线间距5 m，并在隧道壁面及出口共布置4个测点，如图2所示。隧道入口为帽檐斜切式洞门，分别采用 1∶1.00，1∶1.25，1∶1.50，1∶1.75，1∶20共5种斜切斜率(斜切斜率为斜切段高度H与长度L的比值)，如图3所示；隧道出口采用端墙式洞门形式，高速列车表面网格如图4所示。

1.2 动模型试验

动模型试验采用大型列车气动性能模拟动模型试验装置，这是国内最佳的对列车过隧道空气动力问题进行模拟试验研究的专用大型动模型试验设备，根据流动相似原理，通过弹射方式使模型列车在模拟线路上高速运行，真实再现列车高速通过隧道的空气三维非定常流动现象[14-15]。本次动模型试验的模型缩比为1∶20，即动模型采用的模型尺寸为数值计算模型尺寸的1/20，在保证阻塞比一致的同时，高速列车与隧道壁面布点位置按比例与数值模拟计算完全一致。高速列车、隧道模型分别如图5和图6所示。

图1 高速列车模型测点布置图Fig.1 Points arrangement of high-speed train model

图2 隧道模型测点布置图Fig.2 Points arrangement of tunnel model

图3 帽檐斜切式隧道洞门示意图Fig.3 Schematic diagram of hat oblique portal

图4 高速列车网格图Fig.4 Grid of high-speed train model

图5 高速列车模型Fig.5 Model of high-speed train

图6 帽檐斜切式洞门模型Fig.6 Model of hat oblique portal

2 结果分析

2.1 数值计算与动模型试验结果比较

数值计算与动模型试验两者的比较工况为：高速列车以350 km/h速度通过长1 km的双线隧道，该隧道带有斜切斜率为1∶1.25的帽檐斜切式洞门。根据本次数值计算所布置测点情况，车体表面最大瞬变压力变化幅值出现在车头侧窗靠近隧道壁一侧的测点，即车体表面1号测点；隧道壁面最大瞬变压力变化幅值出现在隧道2号测点。表1所示为该工况下车体表面、隧道壁面测点最大瞬变压力变化幅值，隧道出口20 m处4号测点微气压波幅值的数值计算与动模型试验结果比较。以车头鼻尖位置进入隧道为时间零点，根据相似原理，将数值模拟计算所得数据图形的时间轴缩小 20倍，则可与动模型试验的时间同步，图 7～9所示为对应测点压力变化曲线比较结果。

对比数值计算与动模型试验结果可以看出：2种方法得到的瞬变压力及微气压波曲线变化规律基本一致，幅值略有差异，误差在 5%以下，说明所采用的数值计算方法能够较好地模拟列车高速通过隧道引发的空气动力效应问题。

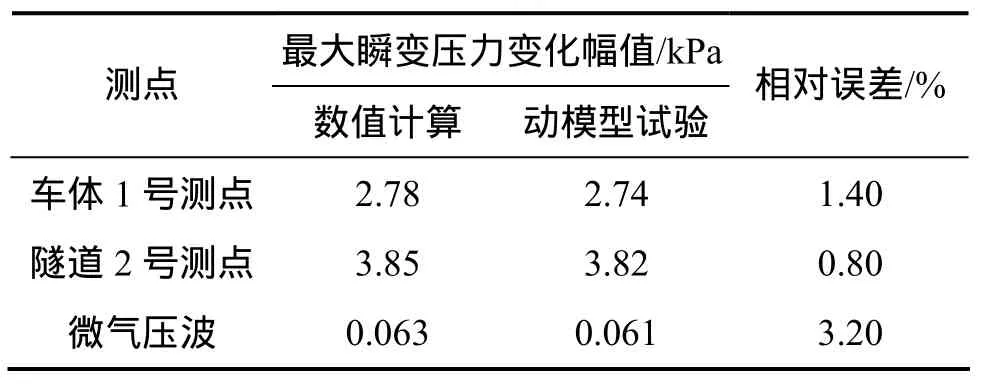
表1 2种方法所得最大瞬变压力变化幅值比较Table 1 Comparison of maximum pressure amplitude for measuring point

图7 车体表面1号测点瞬变压力变化曲线比较Fig.7 Comparison between two curves of transient pressure attained from two methods for measuring point 1 on train

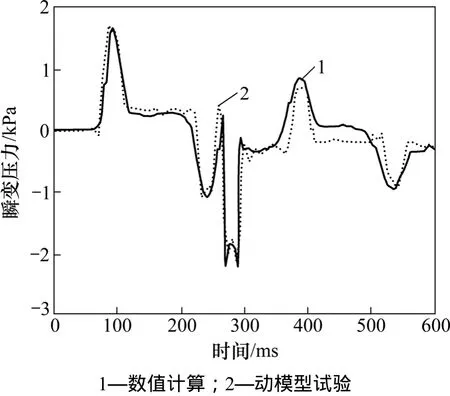
图8 隧道壁面2号测点瞬变压力变化曲线比较Fig.8 Comparison between two curves of transient pressure attained from two methods for measuring point 2 on tunnel

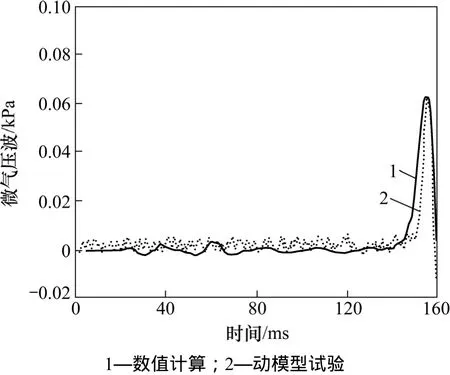
图9 隧道出口20 m处微气压波曲线比较Fig.9 Comparison between two curves of micro-pressure waves attained from two methods for measuring point with distance of 20 m from tunnel exit

以下利用数值计算方法，在上述研究的基础上，重点讨论帽檐斜切式隧道洞门的斜切斜率对隧道空气动力效应的影响。

2.2 车体表面及隧道壁面瞬变压力变化

表2所示为5种斜切斜率条件下高速列车车体表面及隧道壁面测点最大瞬变压力变化幅值比较结果。

由表2可知：在不同斜切斜率条件下，车体表面最大瞬变压力幅值相差为5.3%，隧道壁面最大瞬变压力变化幅值相差1.0%，即车体表面和隧道壁面最大瞬变压力幅值基本不受洞门斜切斜率的影响。这是因为在隧道长度及车速相同的情况下，阻塞比是影响车体表面和隧道壁面瞬变压力变化的重要因素，但在本次研究中采用的车-隧阻塞比相同，而隧道洞门斜切斜率不影响阻塞比，因此，其对车体表面及隧道壁面瞬变压力变化基本无影响。

表2 车体表面及隧道壁面测点最大瞬变压力变化幅值比较Table 2 Maximum pressure amplitude for measuring point on train and tunnel

当列车驶入隧道瞬间，由于空气的压缩性及列车表面与隧道壁面限制了空气流动的空间，使紧贴在列车车头前方的空气受到压缩并随列车向前流动，造成列车前方的空气压力突然升高，产生压缩波，压缩波引起隧道入口1号测点瞬变压力上升，直至到达最大正峰值，形成初始压缩波。图10所示为不同斜切斜率条件下，隧道入口1号测点初始压缩波波形比较结果，图11所示为初始压缩波瞬变压力梯度曲线比较结果，表3所示为初始压缩波最大压力梯度。

由图10 可知：5种斜切斜率的隧道洞门结构下，初始压缩波分ab和cd2个上升阶段，其到达峰值d点的时刻及峰值基本相同，其中ab段对应图11中的第1个压力梯度峰值，cd段对应图11中的第2个压力梯度峰值，而第1个压力梯度峰值基本上决定了隧道出口的微气压波幅值；随着斜切斜率的减小，ab段初始压缩波上升到峰值的时刻滞后，所需时间增加，即其压力梯度最大值减小。可见：隧道洞门结构斜切斜率越小，对瞬变压力梯度的缓解效果越好。

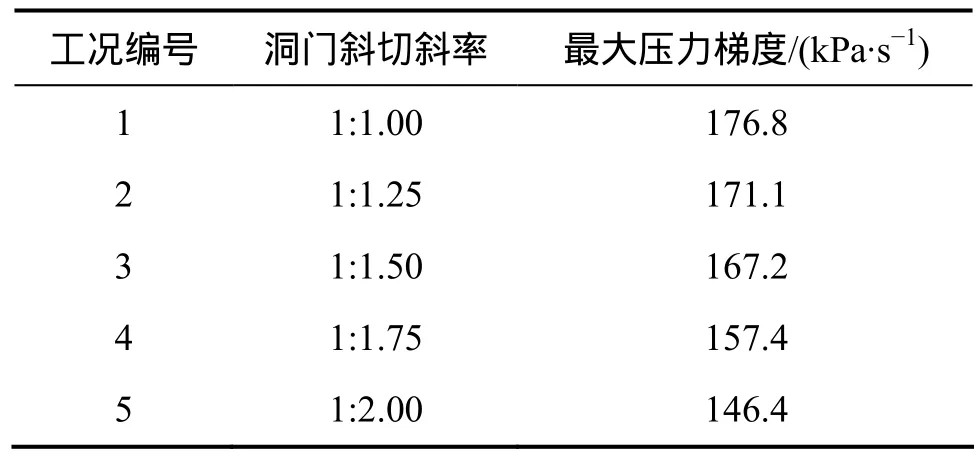
表3 初始压缩波最大压力梯度比较Table 3 Comparison of the largest pressure gradient of initial compression wave

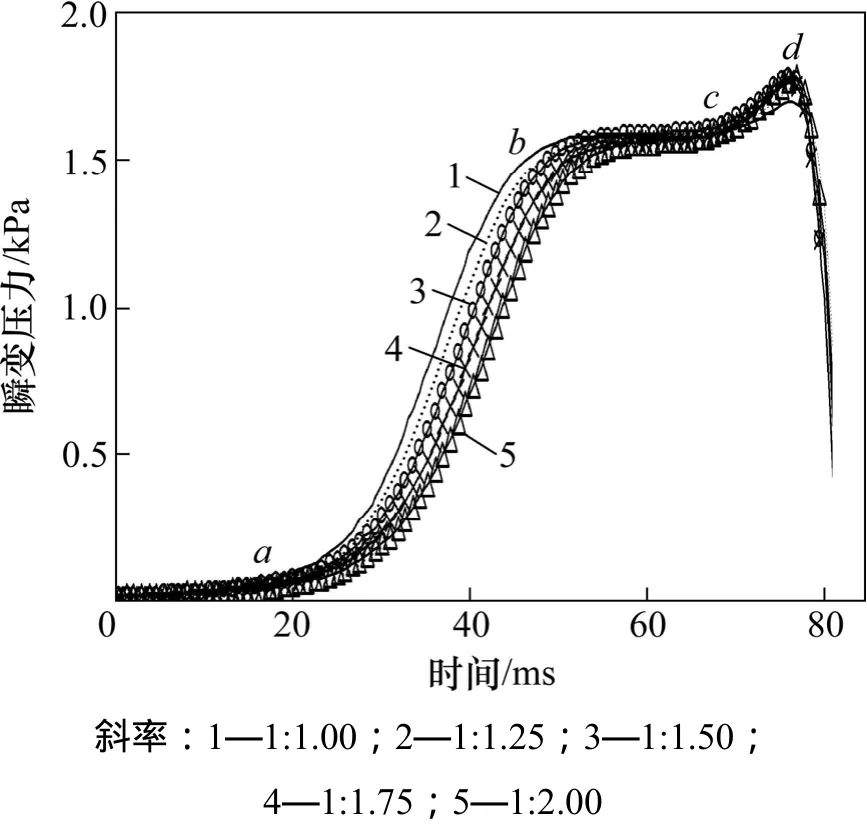
图10 隧道入口初始压缩波曲线比较Fig.10 Comparison of initial compression wave curves

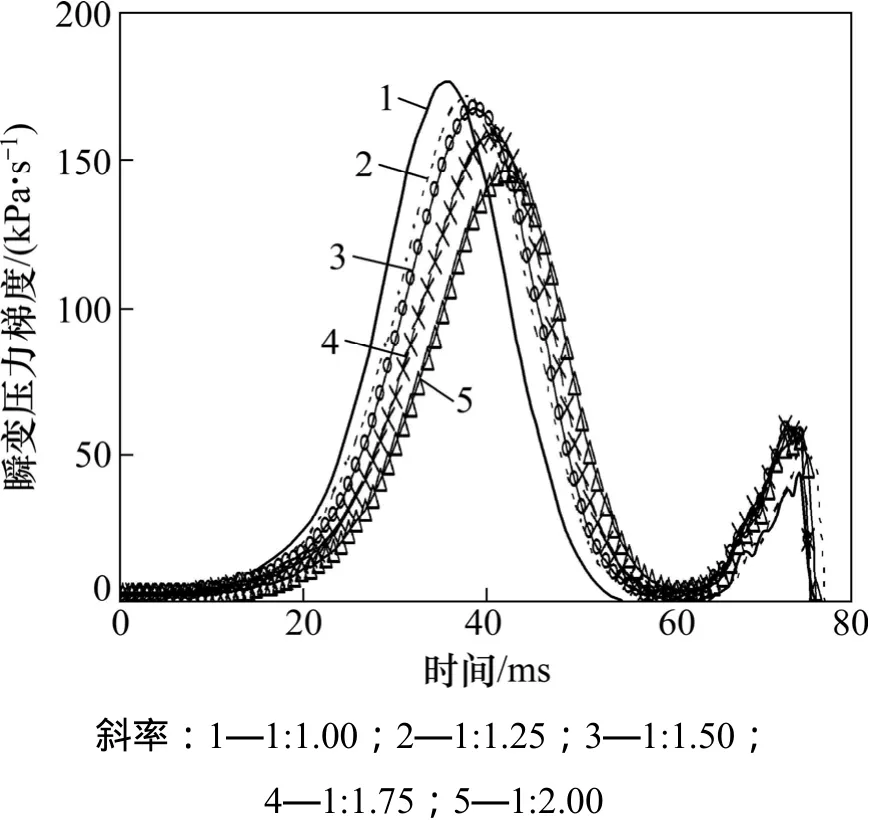
图11 隧道入口初始压缩波瞬变压力梯度曲线比较Fig.11 Comparison of pressure gradient curves

2.3 洞门斜切斜率对微气压波的影响

列车进入隧道形成的压力波不仅引起车体表面和隧道壁面的压力变化，而且在压缩波由隧道口作为冲击波穿出时，会形成噪声，作为微气压波向周围传播。表4和图12所示分别为各工况下隧道出口20 m处测点微气压波幅值及其比较图；各工况下微气压波幅值比较曲线见图13。

从表4、图12和图13可以看出：有效的改变帽檐斜切式隧道洞门的斜切斜率可以显著降低隧道口处微气压波，隧道洞门斜切斜率为1∶1.00时，隧道口处的微气压波幅值最大，为66 Pa；当隧道洞门斜切斜率为1∶2.00时，隧道口处微气压波幅值最小，为54 Pa。相对于斜切斜率为1∶1.00的隧道洞门结构，另外4种斜切斜率下隧道出口微气压波降幅分别为 4.5%，6.1%，12.1%和18.2%。

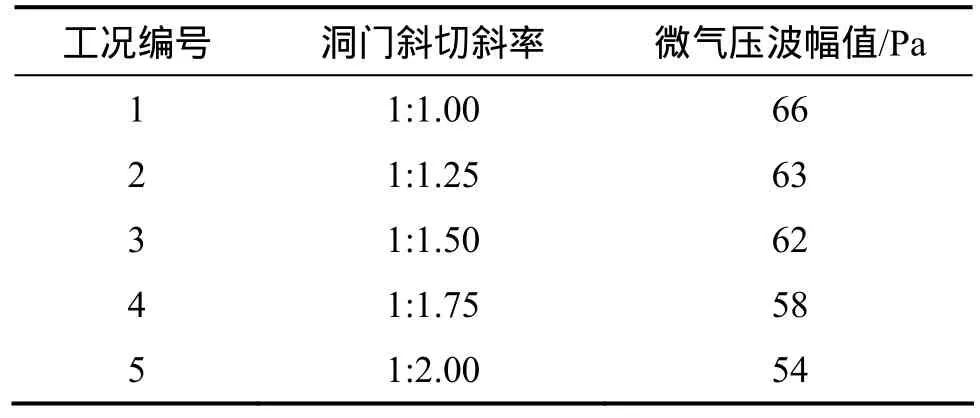
表4 隧道出口测点微气压波幅值比较Table 4 Comparison of maximum pressure amplitude of micro-pressure waves for measuring point on export of tunnel

图12 各隧道洞门结构下微气压波幅值比较曲线Fig.12 Analogy of amplitude for micro-pressure waves

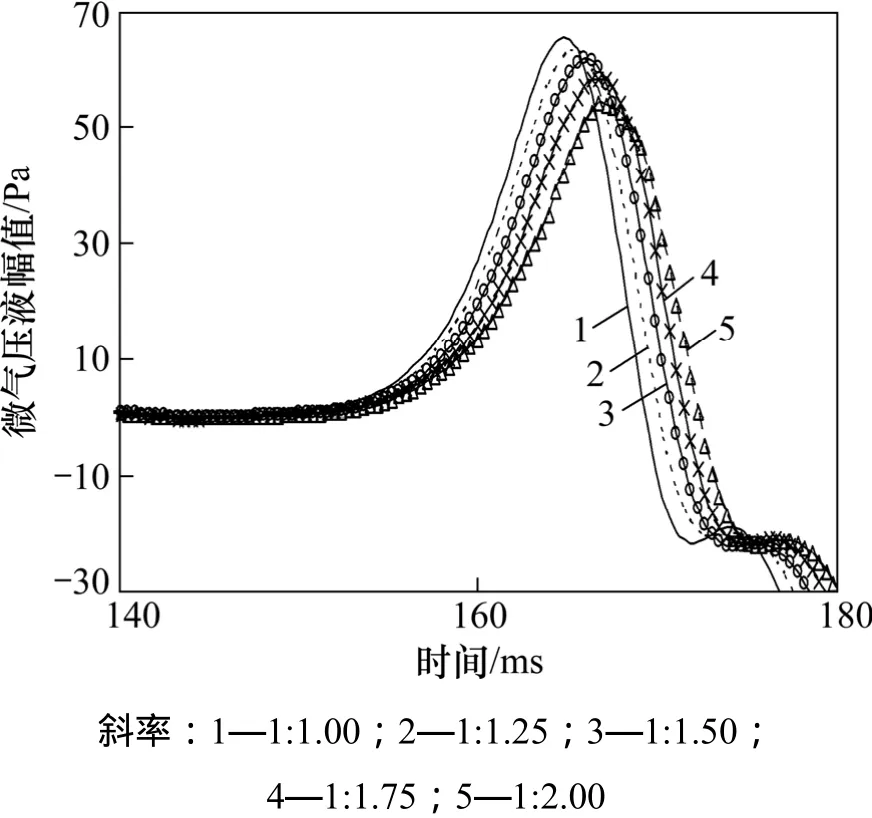
图13 隧道出口测点微气压波压力变化曲线比较Fig.13 Comparison of curves for micro-pressure waves

微气压波幅值减小是因为它的形成与初始压缩波有关，初始压缩波压力上升的过程基本决定了隧道出口的微气压波幅值，而初始压缩波压力上升的过程即为压力梯度的变化过程，因此，隧道口微气压波幅值随压力梯度最大值的减小而减小；随着斜切斜率的减小，初始压缩波压力梯度最大值减小，微气压波幅值减小，即斜切斜率越小，帽檐斜切式隧道洞门对隧道出口微气压波的改善效果越好。

3 结论

(1) 数值模拟与动模型试验 2种方法得到的结果较吻合。2种方法得到的压力曲线变化规律完全一致，仅变化幅值略有差异，相对误差在 5%以下，说明本文采用的数值计算方法能够较好地模拟高速列车通过隧道时所诱发的空气动力效应问题。

(2) 在 5种斜切斜率的帽檐斜切式隧道洞门结构形式下，车体表面测点瞬变压力变化规律、隧道壁面测点瞬变压力变化规律一致；在不同斜切斜率帽檐斜切式洞门条件下，车体表面和隧道壁面最大瞬变压力变化幅值相差较小，最大仅5.3%，即隧道洞门结构的斜切斜率对高速列车车体表面和隧道壁面瞬变压力变化基本无影响。

(3) 当斜切斜率减小时，隧道壁面测点初始压缩波上升到峰值的时刻滞后，瞬变压力梯度最大值减小，说明斜切斜率越小，对瞬变压力梯度的缓解效果越好。

(4) 有效的改变帽檐斜切式洞门结构的斜切斜率可以显著降低隧道口处微气压波，随着帽檐斜切式隧道洞门斜切斜率的减小，相对于斜切斜率为1∶1.00的隧道洞门，隧道出口20 m处微气压波幅值的降幅越来越大，即隧道洞门的斜切斜率越小，其对隧道出口微气压波改善效果越好。

[1]王英学, 高波, 郑长青, 等.高速列车进入隧道产生的微气压波实验研究[J].实验流体力学, 2006, 20(1)∶ 6-8.WANG Yingxue, GAO Bo, ZHENG Changqing, et al.Micro-compression wave model experiment on the high-speed train entering tunnel[J].Journal of Experiments in Fluid Mechanics, 2006, 20(1)∶ 6-8.

[2]Takashi F, Satoru O, Masanobu L, et al.Propagation of compression wave in a long tunnel with slab tracks[J].Quarterly Report of RTRI, 2005, 46(3)∶ 188-193.

[3]刘堂红, 田红旗, 金学松.隧道空气动力学实车试验研究[J].空气动力学报, 2008, 26(1)∶ 42-46.LIU Tanghong, TIAN Hongqi, JIN Xuesong.Experimental study of full-scale train on aerodynamics in tunnel[J].Acta Aerodynamica Sinica, 2008, 26(1)∶ 42-46.

[4]Aoxi T, Matsuo K, Hidaka H, et a1.Attention and distorsion of propagating compression waves in a high-speed railway model and in real tunnel[C]//20th International Symposium on Shock Waves.Marseille, France, 1995∶ 178-184.

[5]Yamamoto A.Aerodynamics of a train and tunnel[C]//Proceedings of 1st International Conference on Vehicle Mechanics.Detroit∶ Society of Automotive Engineers, Inc, 1968∶151-163.

[6]Sockel H.Fluid dynamics and fluid machinery[M].New York∶Wiley, 1996∶ 1721-1741.

[7]Satoru O, Tatsuo M.Tunnel entrance hoods for reduction of micro-pressure wave[J].QR of RTRI, 1988, 29(3)∶ 134-139.

[8]朱克勤, 杨宇光.高速列车穿越隧道时一维非定常流的数值研究[J].空气动力学学报, 1998, 14(4)∶ 480-484.ZHU Keqin, YANG Yuguang.Numerical study on an unsteady one-dimensional flow produced by high-speed trains passing a tunnel[J].Acta Aerodynamica Sinica, 1998, 14(4)∶ 480-484.

[9]骆建军, 高波, 王英学.高速列车突入隧道与缓冲结构时的数值模拟[J].空气动力学报, 2003, 21(3)∶ 376-381.LUO Jianjun, GAO Bo, WANG Yingxue.Numerical study on Tunnel-hood when high-speed train passing a tunnel[J].Acta Aerodynamica Sinica, 2003, 21(3)∶ 376-381.

[10]骆建军, 王梦恕, 高波, 等.高速列车进入带缓冲结构隧道的压力变化研究(I)[J].空气动力学报, 2007, 25(4)∶ 488-494.LUO Jianjun, WANG Mengshu, GAO Bo, et al.Study on the compression wave induced by a high-speed train entering into a tunnel with hood(I)[J].Acta Aerodynamica Sinica, 2007, 25(4)∶488-494.

[11]赵勇, 唐国荣.关于客运专线隧道设计与施工的几点意见[J].铁道标准设计, 2005(6)∶ 128-129.ZHAO Yong, TANG Guorong.Points on tunnel design and construction of passenger dedicated line[J].Railway Standard Design, 2005(6)∶ 128-129.

[12]梁习锋, 熊小慧.4 种车型横向气动性能分析与比较[J].中南大学学报∶ 自然科学版, 2006, 37(3)∶ 607-612.LIANG Xifeng, XIONG Xiaohui.Analysis and comparison of lateral aerodynamic performance on four kinds of cars[J].Journal of Central South University∶ Science and Technology,2006, 37(3)∶ 607-612.

[13]王福军.计算流体动力学分析[M].北京∶ 清华大学出版社,2004∶ 210-215.WANG Fujun.Analysis of computational fluid dynamics[M].Beijing∶ Tsinghua University Press, 2004∶ 210-215.

[14]田红旗.列车空气动力学[M].北京∶ 中国铁道出版社, 2007∶99-101.TIAN Hongqi.Train aerodynamics[M].Beijing∶ China Railway Press, 2007∶ 99-101.

[15]田红旗.中国列车空气动力学研究进展[J].交通运输工程学报, 2006, 6(1)∶ 1-9.TIAN Hongqi.Study evolvement of train aerodynamics in China[J].Journal of Traffic and Transportation Engineering,2006, 6(1)∶ 1-9.