GPS/GLONASS 组合精密单点定位模型探究

魏 勇

（河南城建学院，467036）

0 引言

树木遮挡或地势低洼地区使GPS 接收机接收到的可用信号减少，从而使GPS 精密单点定位的收敛时间增加，精度降低。GPS/GLONASS 组合精密单点定位能够增加可用信号，增加多余观测值，增强几何结构，提高系统的完备性和可靠性。GPS/GLONASS 组合精密单点定位的解算模型主要有两种：UofC 模型和消电离层组合模型。为了获得高精度坐标，还需考虑其他误差改正模型，如天线相位中心偏差等。基于消电离层模型和各种误差改正模型，许多学者开展GPS/GLONASS 组合精密单点定位研究，认为GPS/GLONASS系统较GPS 系统的定位精度和收敛速度有一定改善，尤其是当GPS 可视卫星较少时，GPS/GLONASS 组合系统较GPS 系统改善效果有显著提高。

本文针对GPS/GLONASS 组合精密单点定位消电离层组合模型中待估参数的选取方案进行对比，确定最优方案。根据精度因子指标，验证GPS/GLONASS 系统与GPS 系统的精度关系。最后，利用不同先验权值研究GPS/GLONASS 组合精密单点定位的性能。

1 GPS/GLONASS 组合精密单点定位模型

GPS/GLONASS 组合精密单点定位的观测方程为

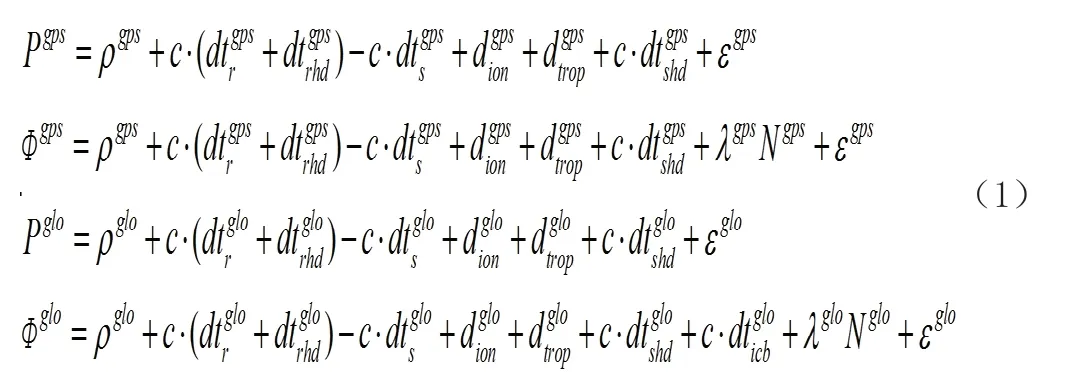
基于Zumberge 提出的消电离层组合模型，GPS/GLONASS 消电离层组合的精密单点定位模型为

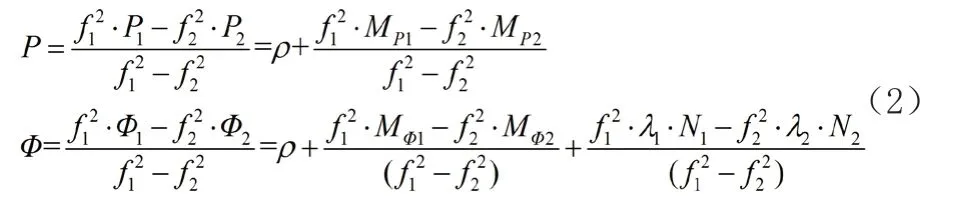
为了获得高精度的接收机坐标，首先需要对各种误差建模改正。GPS 和GLONASS 卫星轨道误差和卫星钟差通过IGS 提供的精密星历和钟差产品改正。其他误差由于两种卫星系统采用的频率不同和计算接收机坐标时刻卫星位置不同而存在差异，如相位缠绕、相对论、地球自转改正、卫星天线相位中心改正和接收机天线相位中心改正。GPS/GLONASS 消电离层组合精密单点定位无法消除对流层延迟，将其作为参数估计。组合系统的模糊度因吸收部分稳定的未检校相位延迟而不具备整周性，故作为参数估计。GPS和GLONASS 卫星信号在接收机高频通道的传播路径不同，产生硬件延迟。GPS 卫星和GLONASS 卫星的硬件延迟不同，使不同卫星系统的信号接收时间基准不同。同时，一些GNSS 接收机针对不同的卫星系统采用不同的接收机钟。在联合数据处理时，要建立不同的时间基准，计算两个系统的接收机钟差。GPS/GLONASS 组合精密单点定位的接收机钟处理方法可分为两种：

（1）GPS 接收机钟差和GLONASS 接收机钟差分别作为参数估计，则待估参数向量为

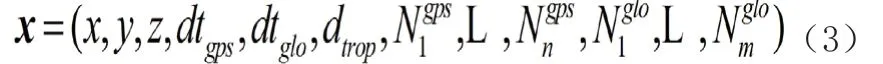
（2）GPS 接收机钟差和GPS/GLONASS 接收机钟差之差分别作为参数估计，则待估参数向量为

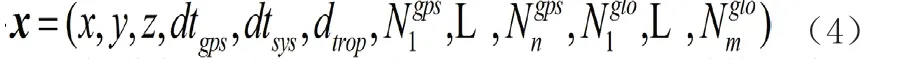
两种接收机钟差估计方案只与观测方程的系数矩阵有关，方案（1）的系数矩阵为

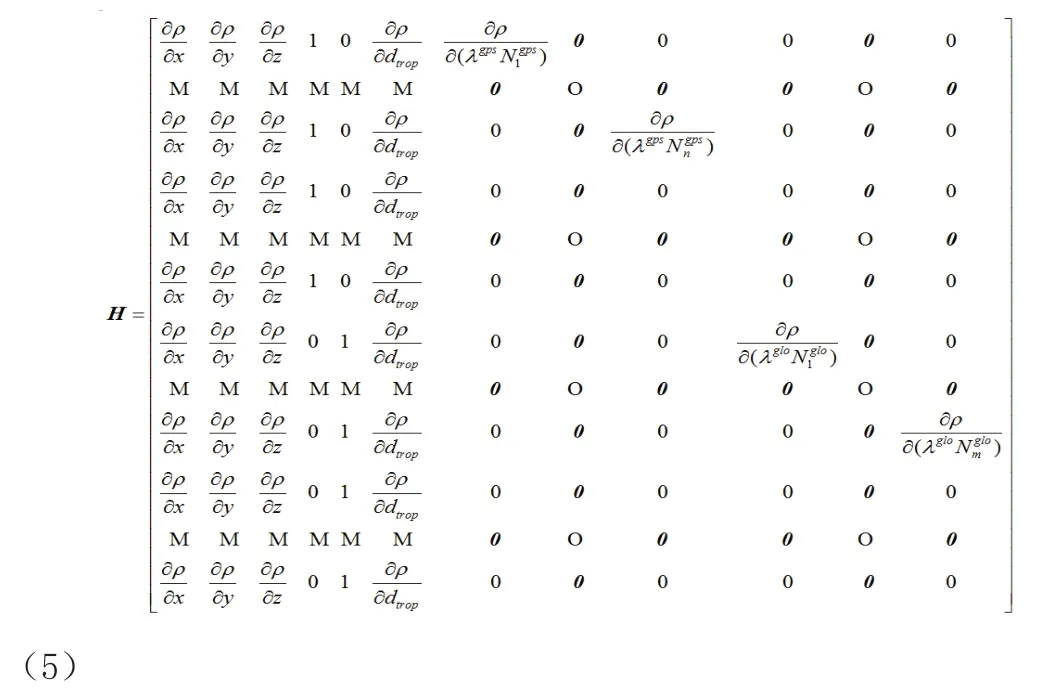
两种方案消电离层组合且添加各项改正后的观测值为：

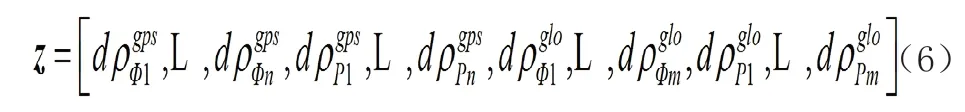
上述各变量确立之后，利用最小二乘或卡尔曼滤波进行参数估计，获得接收机坐标。

2 实验分析

以北京站2011年第66 天3个小时数据为例（11:00:00～14:00:00），IGS 提供的15min 间隔精密轨道和钟差星历用于改正轨道误差和卫星钟差。GPS 和GLONASS 可视卫星见图1。圆环代表卫星的方位角，射线代表卫星高度角。当卫星截止高度角设为15°时，GPS 可视卫星一般为6 颗左右，GPS/GLONASS 组合系统的可视卫星数维持在10 颗以上。增加了多余观测数，完善卫星几何分布结构，能够增强解算的可靠性和精度。从精度因子可知（图2），除了初始几个历元，GPS 系统的各种精度因子（DOP）值在0.5～2 之间，且卫星数的变化明显影响DOP。卫星数增加时，DOP 有所提高，而卫星数减少时，DOP 降低。同样的趋势也在GPS/GLONASS 组合系统中呈现，但GPS/GLONASS 组合系统比GPS 系统的各种DOP 值有所提高，基本维持在0.3～1.5 之间。

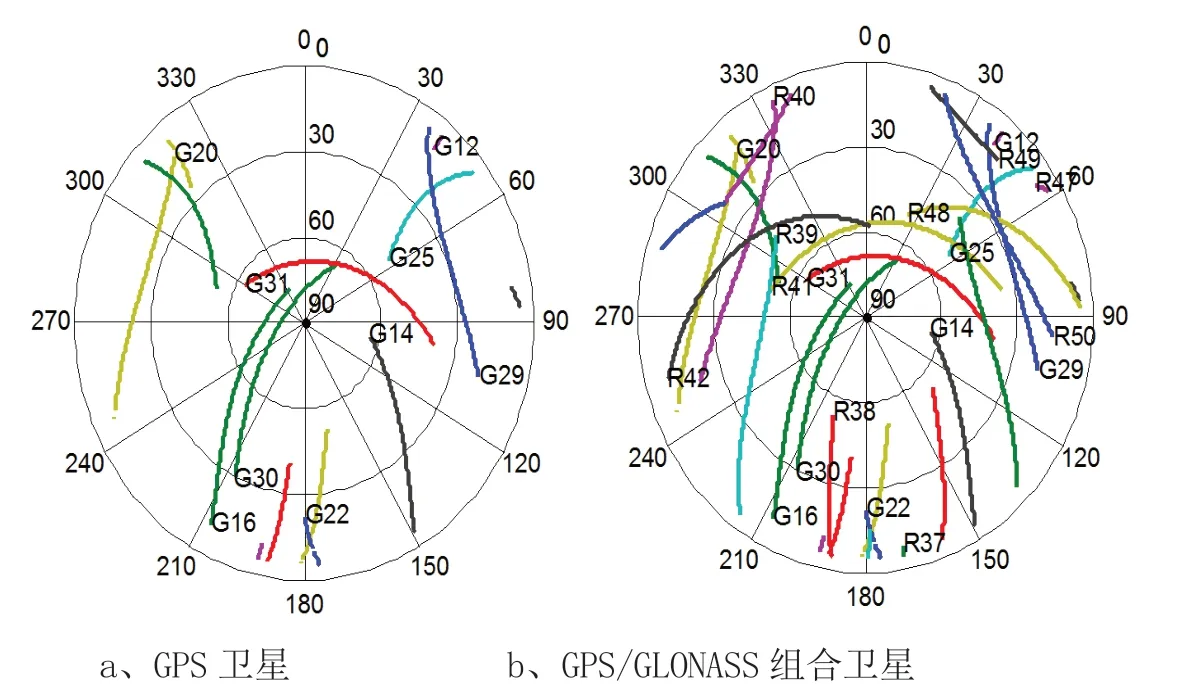
图1 卫星天空可视图（G 代表GPS 卫星；R 代表GLONASS 卫星；数字代表卫星号）Fig.1 Sky plot of GPS and GLONASS satellites

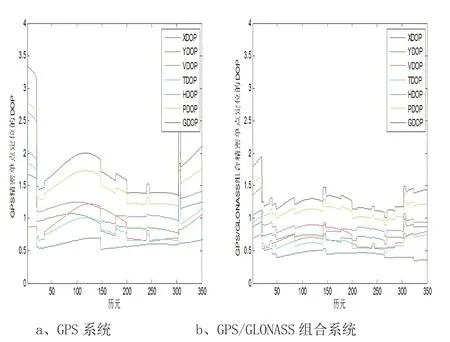
图2 精度因子Fig.2 Dilution of precision

本文采用两种模型解算接收机坐标和钟差：GPS 接收机钟差和GLONASS 接收机钟差分别作为参数估计；GPS 接收机钟差和GPS/GLONASS 时间基准差分别作为参数估计。GLONASS 接收机钟差作为参数估计的结果见图3 上部，随着历元的不断增加，GLONASS 钟差不断增大，降低计算机的存储和计算效率。而估计的GPS/GLONASS 时间基准差具有一定的稳定性（图3 下部），体现GLONASS 时间基准与GPS 时间基准之间的差异。图4 上部为GLONASS 接收机钟差作为参数解算的接收机坐标，与GPS/GLONASS时间基准差作为参数解算的接收机坐标相同（图4 下部）。另外，两种模式解算的GPS 接收机钟差相同。

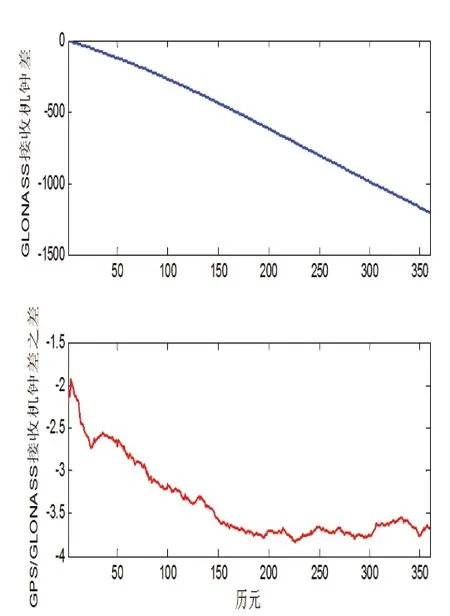
图3 两种模型估计的接收机钟差接收机坐标Fig.3 Receiver clock error estimated by two models

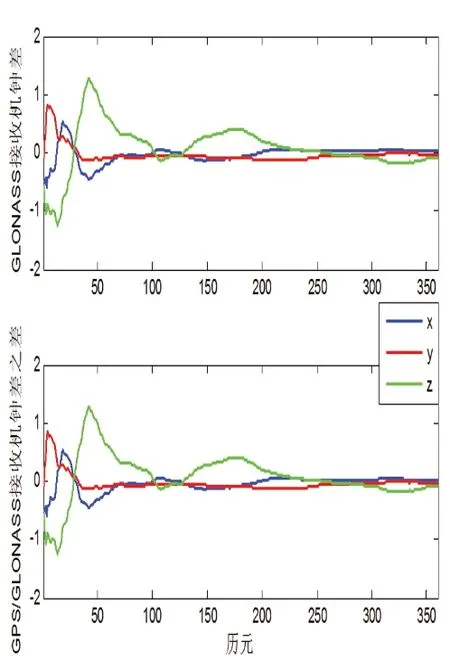
图4 两种模型估计的Fig.4 Receiver coordinates estimated by two models

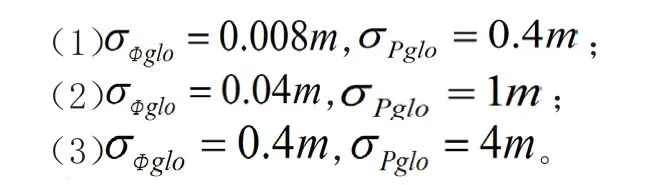
实验结果如图5。当采用方案（1），即GPS 和GLONASS 观测值精度相同时，GPS/GLONASS 组合系统不仅降低GPS 的解算精度，而且增加解算的不确定性。原因是GLONASS 观测值或其精密轨道和钟差产品的精度低于GPS 观测值或其精密轨道和钟差。当采用方案（3）时，GLONASS 先验精度较低，虽然收敛前期能够加快收敛速度，但是解算精度无法提高。当采用方案（2）时，不仅加快了组合系统的收敛速度，而且一定程度上提高了解算精度（图5 中红线与其他颜色相比）。GLONASS 观测值先验标准差不同，导致张小红和孟祥广得出略有差异的结论。

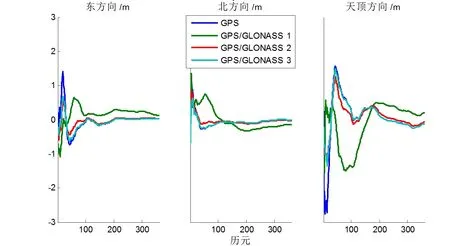
图5 不同权重解算结果对比Fig.5 Comparison resolved by different weight ratio

3 结论

1）虽然将GPS 接收机钟差和GLONASS 接收机钟差作为参数解算的结果与GPS 接收机钟差和GPS/GLONASS 时间基准差作为参数解算的结果相同，但是后者能够节省减少解算参数的数量级，且呈现一定的稳定性；

2）由于GPS 和GLONASS 系统站星间距离观测精度存在差异，随机模型影响GPS/GLONASS 组合精密单点定位的解算精度。在联合数据处理时，应采用算法赋予两者不同的权重比。

[1] 许长辉,王坚,高井祥.GNSS 导航平台数据处理的可靠性分析.大地测量与地球动力学.2009,29(1):114-118.Xu Changhui,Wang Jian,Gao Jingxiang.Analysis of Reliability of Data Processing of GNSS Navigation Platform.Journal of Geodesy and Geodynamics.2009,29(1):114-118.

[2] 蔡昌盛.GPS/GLONASS 组合精密单点定位理论与方法[D].徐州:中国矿业大学,2008.Cai Changsheng.Theory and Method of Combined GPS/GLONASS Precise Point Positioning.Xuzhou:China University of Mining &Technology Press,2008

[3] Zumberge J F,Heflin M B,Jefferson D C,et al.Precise point positioning for the efficient and robust analysisof GPS data from large networks[J].Journal of Geophysical Research,1997,102(B3):5005-5017.

[4] 李晓波,王小亚,任金卫.GNSS 天线相位中心偏差与变化精确标定方法研究.天文学进展.2012,30(4):501-517 Li Xiaobo,Wang Xiaobo,Ren Jinwei.Research on Calibration Methods of GNSS Antenna Phase Center OfFsets and Variations.Progress in Astronomy.2012,30(4):501-517.(in Chinese)

[5] 张小红,郭斐,李星星等.GPS/GLONASS 组合精密单点定位研究.武汉大学学报:信息科学版.2010,35(1):9-12.Zhang Xiaohong,Guo Fei,Li Xingxing,et al.Study on Precise Point Positioning Based on Combined GPS and GLONASS.Geomatics and Information Science of Wuhan University.2010,35(1):9-12

[6] 孟祥广,郭际明.GPS/GLONASS 及其组合精密单点定位研究.武汉大学学报:信息科学版.2010,35(2):1409-1413.Meng Xiangguang,Guo Jiming.GPS/GLONASS and Their Combined Precise Point Positioning.Geomatics and Information Science of Wuhan University.2010,35(2):1409-1413

[7] 王正军.GPS/GLONASS 组合精密单点定位性能分析.大地测量与地球动力学.2012,32(2):105-109.Wang Zhengjun.Performance Assessment of GPS/GLONASS Precise Point Positioning.Journal of Geodesy and Geodynamics.2012,32(2):105-109

[8] 许长辉.高精度GNSS 单点定位模型质量控制及预警.徐州:中国矿业大学出版社,2011.XU Changhui.Modeling Quality Control and Warning System of High-Accuracy GNSS Point Positioning .Xuzhou:China University of Mining &Technology Press,2011