可回售可赎回可转换债券的定价分析

蒋致远，张顺明 ，李江峰

（1.厦门大学 经济学院，福建 厦门 361005；2.中国人民大学 财经学院，北京 100083；3.桂林电子科技大学 统计系，广西 桂林 541004）

0 引言

债券中经常会包含一种或数种内嵌期权（Embedded Options），当债券中包含的期权和债券无法分割时，称为“内嵌期权”。可提前赎回债券（Callable Bonds）就是属于这种类型，这种债券允许发行人根据一组预先设定的赎回价格（Callable Price）来赎回债券，即内嵌了一个赎回权。可回售债券（Putable Bonds）也是如此，这种债券允许投资者根据一组预先设定的回售价格（Putable Price）把债券回售给发行人。

本文对付息的可回售可赎回可转换债券进行定价分析。利用对冲的方法建立其定价模型，并利用反应扩散方程导出其定价解析式。然后在此基础上，本文得到了另外两种常见的债券——零息的可回售可赎回可转换债券以及付息的可赎回可转换债券定价模型及其解析式。最后，本文对付息的可回售可赎回可转换债券的理论价值关于各参数进行了弹性分析。

1 可回售可赎回可转换债券分析

1.1 标准的可回售可赎回可转换债券分析

在实际的转债市场中，有多种多样的转债，本文选择较为复杂的可回售可赎回可转换的债券为研究对象，鉴于不同具体的条款对价值组成分析不一样，本文采用比较标准的条款，具体为：（D1）回售条款：在其存续期内，只有当标的股价下跌到预先设定的回售触发价格以下时，债券持有者才有权按照预先约定的回售价格执行回售权，回售价格恒定。（D2）赎回条款：在其存续期内，只有当标的股价上涨到预先设定的赎回触发价格以上时，债券发行者才有权按照预先约定的赎回价格执行赎回权，赎回价格恒定，无赎回通知期。（D3）转换条款：在其存续期内，持有者有权在任意时刻按照预先设定的转换价格执行转换权，转换价格恒定。（D4）债息条款：①发行者需要定期向持有者按票面利率支付利息；②若持有者执行转换权，那么他将不再获得当时的累计债息（螺丝条款Screw Clause）。（D5）没有锁定、重置条款以及其他非标准化条款。

1.2 可回售可赎回可转换债券投资分析

可赎回债券给予发行人以事先规定的价格提前买回债券的权力，这种情况一般出现在利率下降、债券价格上升的时候。由此可知，发行人持有的赎回权是一个在标的价格上升的时候购买标的资产的权力，所以它是一个看涨期权。在发行人持有赎回权的情况下，会限制投资者因为债券价格上涨而获得的利润。在可赎回债券与对应的普通债券之间，存在一种重要的关系。所谓“对应”是指除了赎回条款之外，两种债券的其他性质完全相同。即发行人持有期权的多头，投资者持有期权的空头。可回售债券则给予投资人以事先规定的价格将债券提前卖还给发行人的权力，这种情况一般出现在利率上升、债券价格下降的时候。由此可知，投资者持有的回售权是一个在标的价格下跌的时候出售标的资产的权力，所以它是一个看跌期权。在存在回售条款的情况下，投资者人有权根据设定的价格出售债券，这将限制投资者因为利率上升而遭受的损失。此时在可回售债券与对应的普通债券之间，也存在一种重要的关系。即发行人持有期权的空头，投资者持有期权的多头。

由于可转债的债和权益的双重性。对于投资者而言，首先通常债券支付的当期利率一般高于股票的红利率，因此与普通股相比有更高的收益；其次由于存在债券的特性，可转换债券持有者的权益会明显高于普通股的投资者，在股价下降到回售触发价时，可以回售来保护投资者，即使在破产时，持有者的本金也会优先得到支付，因而此类可转换债券在享受企业业绩成长带来的收益是的同时还提供了经济形势不好时的利益保护。对于发行公司而言，可转换债券除了能以较普通债券较低的利率融资外，在二级市场和企业状况不佳时，可以避免大量转股造成的公司每股业绩的稀疏，进而引发的二级市场股票价格的大幅下跌，而利率在股票价格上扬触发赎回机制时，可以赎回转债，保护公司利益。在上述假设基础上，参照Ingersoll(1997)，根据无套利机会原则可知，投资者最优策略为：在到期之前的每一个时刻点，不会主动执行转换权，除非发行者宣告执行赎回权或到期时转换价值大于债券的剩余价值，而当标的股票下跌到触发回售价时，投资立刻回售；对于发行者而言，在剩余存续期内只要标的股票价格上涨到赎回触发价，发行者立刻宣告执行赎回权。另外值得注意的是由于转债的权益性，其票面利率一般要低于相应的普通债券的票面利率。

2 付息的可回售可赎回可转换债券定价分析

2.1 理论假设

考察一份上述可回售可赎回可转换债券。以M,K1,K2,K3,P1,P2,T,r,rf,St分别表示其面值、回售触发价格、赎回触发价格、转换价格、回售价、赎回价、剩余期限、票面利率、无风险利率和t时期标的股票的价格，显然有关系式：K1＜K2＜K3，P1＜P2。为简洁起见，不妨令M=1，当前时刻为零时刻，并以S0,ST表示标的在当前和到期时刻的价格。V(S,t,r),B(S,t,r)分别表示可回售可赎回可转换债券和对应的普通债券的当前理论价值。

基本假设：

（A1）资本市场市场无摩擦；存在连续无风险利率rf，期限结构是水平的不存在无风险套利机会股价服从几何布朗运动：

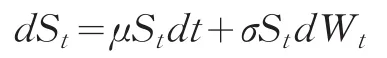
其中Wt表示定义在完备概率空间的标准的布朗运动，μ,σ分别表示瞬时期望收益率和瞬时波动率。

由于本文将涉及到Black-Sholes期权模型框架，定价模型基于单因子无套利模型，在利率取值合理范围内，与多因子模型定价差异很小，也可以吻合本文无风险利率期限结构是水平的假设。

（A2）发行者和持有者都是理性的，而且总是偏好更多的财富；同时都具有对称市场理性，也即都能理性的预期到对方的最优决策。

（A3）潜在的稀疏效应（dilution effect）已经反映到当前的标的股价之中；也即当持有者执行转换权，不会导致标的股价出现骤然下跌。

2.2 建立模型

为定价分析方便，用V表示该债券的内在价值，构造投资组合Π：购买一份可回售可赎回可转换债券，同时卖出Δ份标的股票。那么：

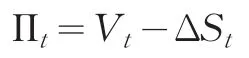
并适当选取Δ，使得投资组合Π在时间段(t,t+dt)是无风险的，投资组合Π的回报率为：

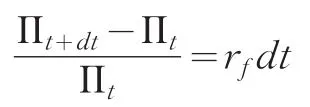
进而有：

dVt=[rf(Vt-ΔSt)+μΔSt]dt+σΔStdWt另一方面，由Ito公式可得：

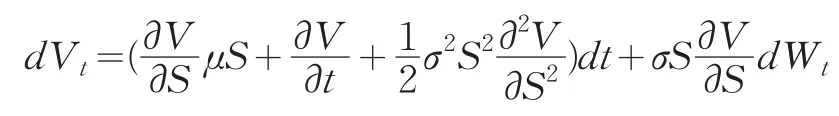
结合上述两式，在风险中性世界可得dWt前面的系数必须为零，从而从而可得可转换债券的价值V满足的扩散方程为

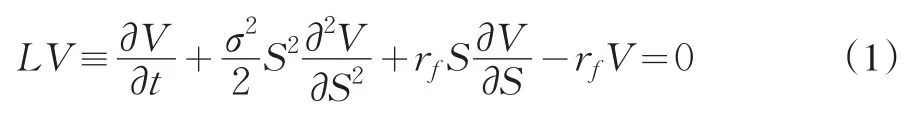
由于可转债的价值有强烈的路径依赖性，那么针对各个条款所对应的是方程的边界条件：

（1）当在 (0,T)任意时刻t(tn≤t＜tn+1)，n=0,1,2,…,N,tN=T,t0=0，标的股价上涨到赎回触发价K3时（其中tn为第n个利息支付日），发行者将立即宣布赎回，从而导致投资者行使转换权并套现，于是得边界条件：

（2）当在 (0,T)任意时刻t(tn≤t＜tn+1)，标的股价下跌到触发价K1时，投资者立即回售，于是得到边界条件：

（3）到期日t=T，当可转债的转换价值大于债券的剩余价值时投资者就转换，否则不转换，于是得到边界条件：

其中K*3=K2(1+r)，于是可回售可赎回可转换债券的价值应满足反应扩散方程定解模型：

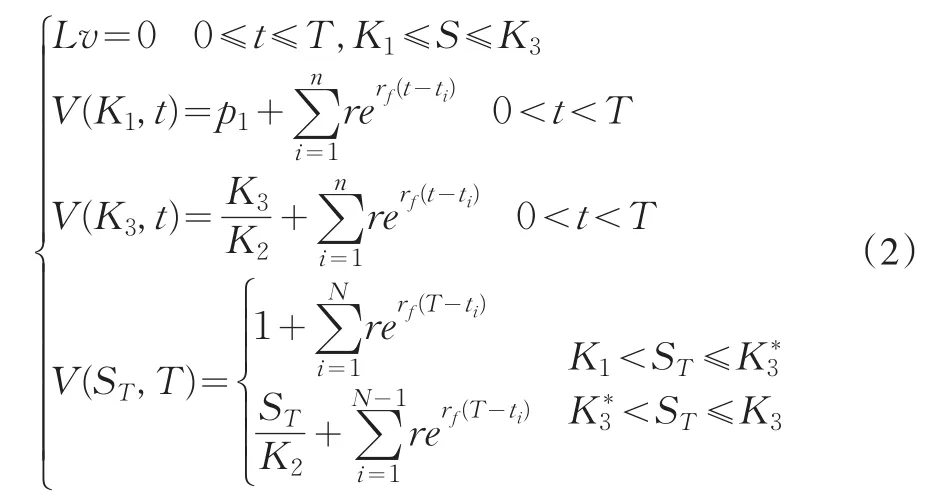
2.3 模型求解

对方程（2）作变量代换x=ln(S/K1),u=K1V，再作函数变换u=eαx+β(T-t)w，其中，在此变换下，可得到w适合的定解问题：

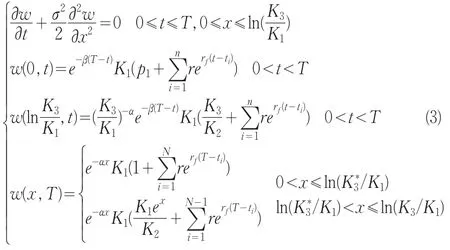
这是一个混合热传导方程，为便于求解，需要先将边值化为零，为此令其中，于是通过对初始条件和f(x,t)作奇延拓，方程（3）的解为：

再把上述的变换都替代回来，可得：

其中

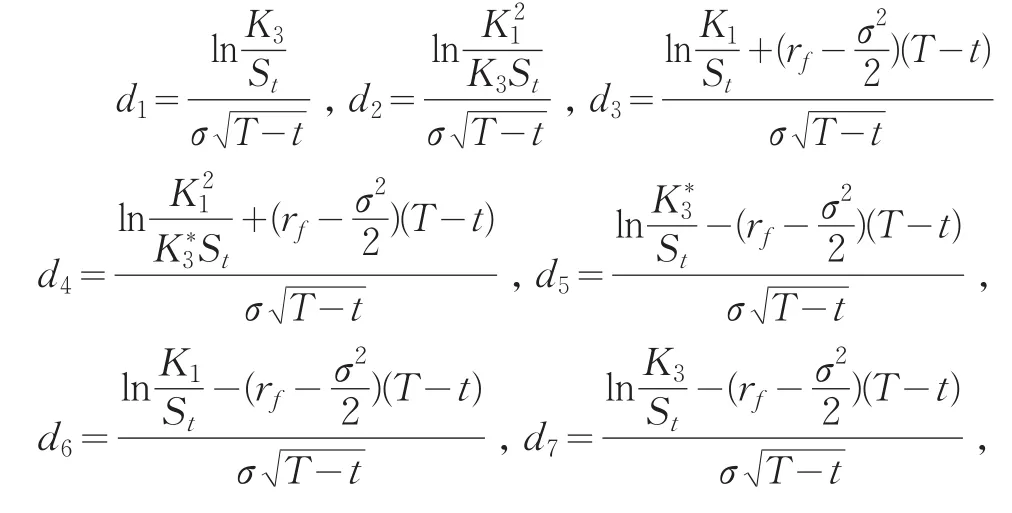
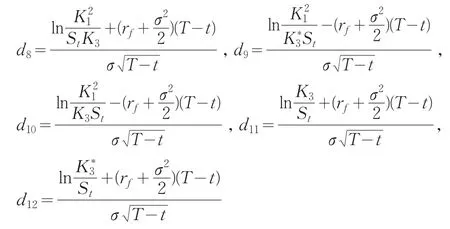
定理1若标的股票服从几何布朗运动，在债券上述条款下，则付息可回售可赎回可转换债券在当前0时刻的理论价值为(4)式。

3 付息的可回售可赎回可转换债券定价模型衍化

3.1 零息的可回售可赎回可转换债券定价分析

如果可转债是零息债券，只要修改模型中的初边值条件。

（1）当在(0,T)任意时刻标的股价上涨到赎回触发价K3时,发行者立即宣布赎回，从而导致投资者行使转换权并套现，于是得边条件：

（2）当在(0,T)任意时刻标的股价下跌到触发价K1时，投资者立即回售，边界条件：

V(K1,t)=p1

中国石油和化学工业联合会副秘书长庞广廉在会上作了题为贸易摩擦下的石化行业国际产能合作及国际合作创新的演讲，约30家出口基地成员出席授牌仪式和培训。

（3）到期日t=T，当转债的转换价值大于债券的剩余价值时投资者就转换，否则不转换，于是得到边界条件：

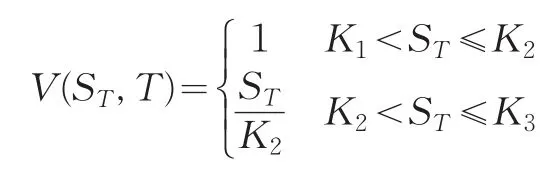
从而满足的系统为：

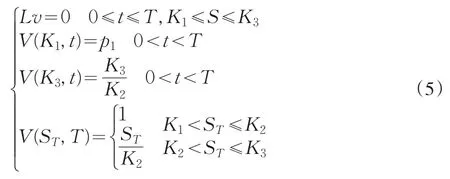
于是可求出其解为：

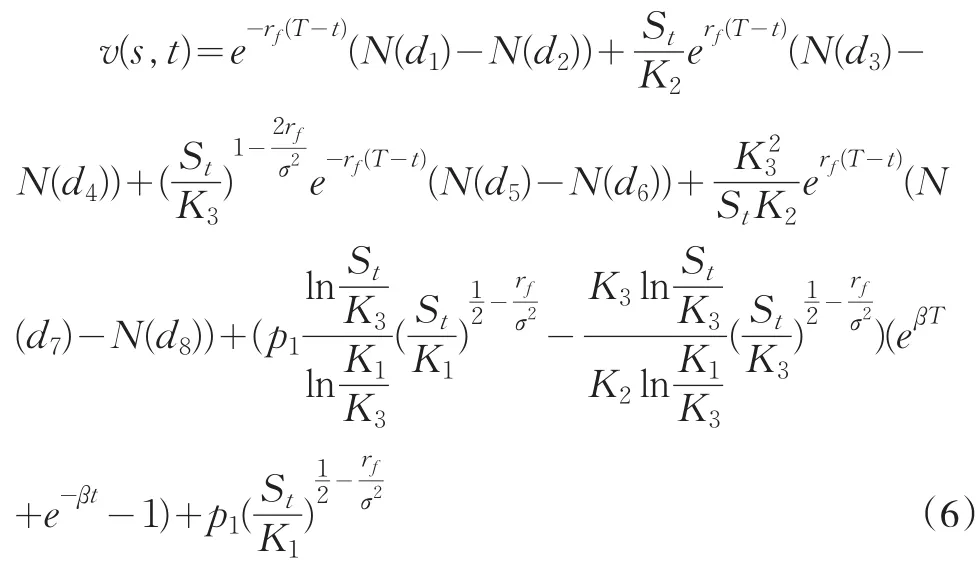
其中

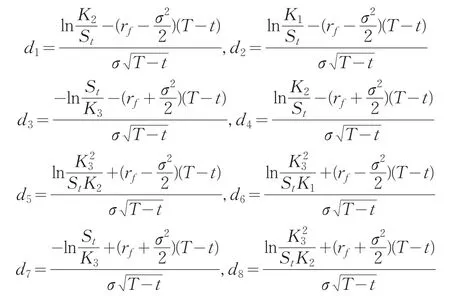
推论1若标的股票服从几何布朗运动，在债券上述条款下，零息可赎回可回售转债的理论价值为（6）式。

3.2 付息的可赎回可转换债券定价分析

若上述转债没有可回售条款的付息债券，那么沿用前面的记法和分析，可以导出付息可赎回可转换债券的定价模型为：

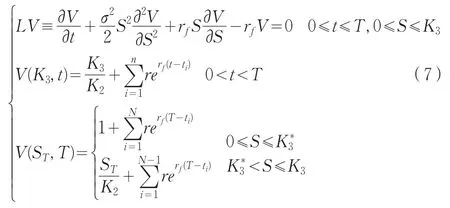
类似的方法可以得到转债的理论价值的解析式：

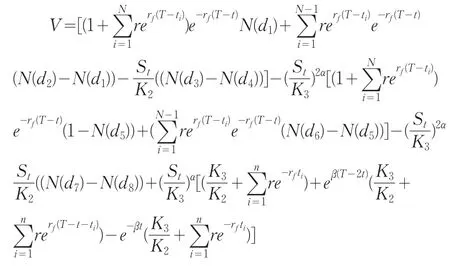
其中

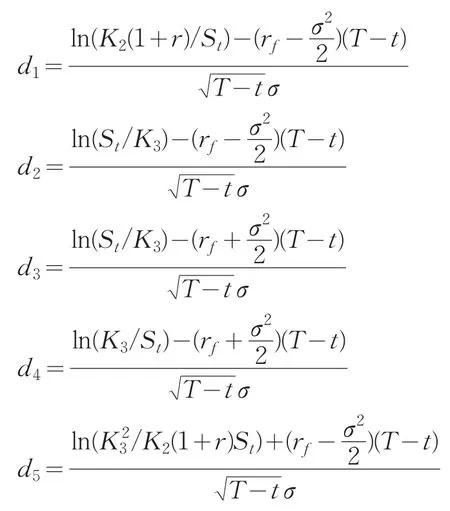
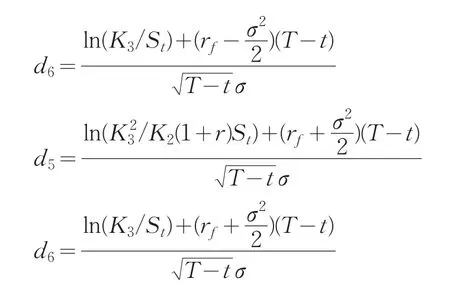
定理2若标的股票服从几何布朗运动，在债券上述条款下，付息可赎回可转换债券在当前时刻0的理论价值为（7）式。

4 弹性系数分析

值得注意的是，付息可回售可赎回的转债的理论价值关于参数理论价值对各参数的偏导数的符号为：

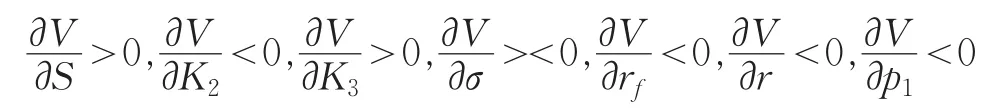
从经济意义上说明：转债券的理论价值在其他条件不变的情况下，转换率越高其理论价值越高，从而定价越高；而同时对赎回触发机制而言，赎回触发价越高，转债的理论价值越高；对于标的股价而言在其他条件一样时，当前股价越低，转债的理论价值越高，这就有异于普通债券和普通股票的理论定价分析了；对于转债的票面利率来说，票面利率越高，转债的理论价值越高；无风险利率越高，转债的价值越低；而回售价越低，转债的价值越低；转债关于标的股票的年波动率的变化趋势关系不明晰，或者说不一定。

对于付息可赎回转债而言，

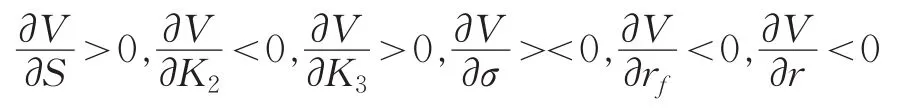
从经济意义上说明：付息可赎回可转换债券的理论价值在其他条件不变的情况下，转换率越高其理论价值越高，从而定价越高；而同时对赎回触发机制而言，赎回触发价越高，转债的理论价值越高；对于标的股价而言在其他条件一样时，当前股价越低，转债的理论价值越高，这就有异于普通债券和普通股票的理论定价分析了；对于转债的票面利率来说，票面利率越高，转债的理论价值越高；无风险利率越高，转债的价值越低；转债关于标的股票的年波动率的变化趋势关系不明晰，或者说不一定。

由前述的最优策略分析发现，在赎回价处于合理的范围之内，不会对转债有影响，因为在赎回触发时，投资者就会行权转换，从理性的角度来说，债券不可能把赎回价设置为对投资者而言赎回价值高于转换价值之处。

5 结论

本文利用对冲的方法对付息的可回售可赎回可转债券进行了定价分析。首先，对付息的可回售可赎回可转债券的进行投资分析；然后，在合理理论假设的基础上，本文建立了付息的可回售可赎回可转债券的理论模型，并求解得到其解析式；在此基础上，本文根据类似的方法，对另外两种常见的可转债——零息的可回售可赎回可转换债券和付息的可赎回可转换债券进行了定价分析；最后，本文对付息的可回售可赎回可转换债券的理论价值关于各参数进行了弹性分析。分析结果表明：可回售可赎回的转债可以拆解为普通转债、以赎回价为执行价格的上升敲入看涨期权和以回售价为执行价格的下降敲入看跌期权的组合；而付息可赎回转债可拆解为普通转债和以赎回价为执行价格的上升敲入看涨期权的组合。

[1]Kimura T,Shinohara T.Monte Carlo Analysis of Convertible Bonds with Reset Clauses[J].European Joural of Operational Research,2006,168.

[2]Broadie M,Detemple J.American Capped Call Options on Divi⁃dend-Paying Assets[J].The Review of Financial Studies,1995,8(1).

[3]Jonathan E,Ingersoll Jr.A Continent Claim Valuation of Convertible Securities[J].Journal of Financal Economics,1977,4.

[4]Yagi K,Sawaki.The Valuation and Optimal Strategies of Callable Con⁃vertible Bonds[C].Technical Report of the Nanzan Academic Society of Mathematical Science and Information Engineering,2004.

[5]郑晓阳，官畅.随机参数股价波动源模型下可赎回可转债定价[J].哈尔滨工程大学学报，2011,(1).

[6]周其源，吴冲锋，陈湘鹏.付息可赎回可转换债券定价解析式：完全拆分法[J].中国管理科学,2007,15（2）.