预应力约束混凝土梁的研究分析

潘金和，彭 景

(贵州大学空间结构研究中心，贵州贵阳550003)

在现行《混凝土结构设计规范》(以下简称《规范》)[1]中，混凝土极限应变为0.0033。事实上，只需采取适当构造措施，设置附加约束钢筋(图1)，在纵筋及箍筋的约束之下，便可提高混凝土的极限应变及极限强度，从而保证受压区混凝土的延性。

普通混凝土受弯构件，在受拉区配置过多的纵筋后，将会出现超筋破坏。为避免出现超筋破坏，《规范》给定最大配筋率指标。但研究发现，在梁中配置约束钢筋，可以改善受压区混凝土的性能，能提高梁的极限承载力和刚度，荷载不变时可减小梁的高度，从而使房屋获得更大有效空间[2]。

对约束混凝土构件施加预应力，能充分发挥约束混凝土和预应力结构的优点:降低构件变形、抑制构件开裂，增加构件有效高度，提高构件刚度及承载力。如此一来在荷载不变的前提下，便可降低梁的高度，降低建筑造价，获得更大的建筑使用空间。这一基于约束混凝土特性提出的新型结构构件形式，可应用于各种工程结构，具有广泛的应用前景和推广价值。

1 基本构造及性能分析

在普通混凝土梁内配置约束钢筋⑥及增加纵筋②后，成为约束混凝土梁，见图1。

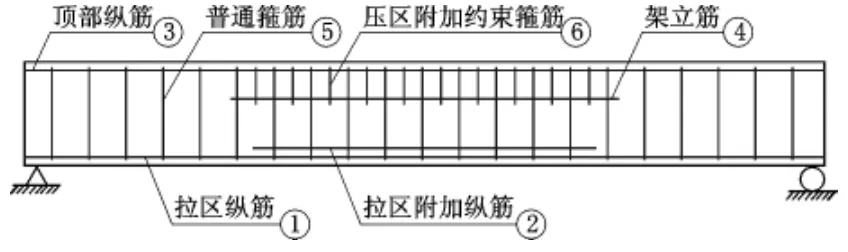
图1 约束混凝土梁示意

在约束混凝土梁上施加预应力，便形成预应力约束混凝土梁。

对于普通混凝土梁，规范规定为避免受压区混凝土受到较大的正应力而发生脆性破坏，普通混凝土梁纵向受拉钢筋屈服与受压区混凝土破坏同时发生时，相对界限受压区高度ξb按《规范》6.2.7－1式计算。

在强约束条件下，约束混凝土的极限应变εc较普通混凝土应变εcu已经有了提高，此时相对界限受压高度ξb必然增大，截面受压区混凝土高度增大。由于约束后的约束混凝土极限强度与此时的最大受压区高度均变大。故而由《规范》6.2.10－1式计算所得的承载力明显提高。

假定分析条件:梁截面尺寸b×h=250×500 mm2，有效高度h0=440 mm。混凝土强度等级为C30，fc=14.3 N/mm2，EC=3.0×104N/mm2，纵筋用 HRB400、箍筋用 HPB300，fy=360 N/mm2，fyv=270 N/mm2，ES=2.0×105N/mm2。

根据以上条件进行后文的分析计算。

1.1 承载力与受压区配箍的关系

根据Murat-Saatcioglu[3]的研究结果，约束混凝土的强度和应变与普通混凝土的强度、应变、配箍情况有如下关系。

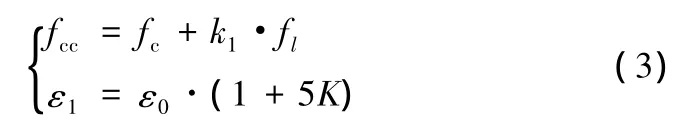
式中:fc为混凝土抗压强度;ε0为混凝土压应变，最小值取为0.002;k1为约束系数，fl为约束应力，K为系数，按下式计算:

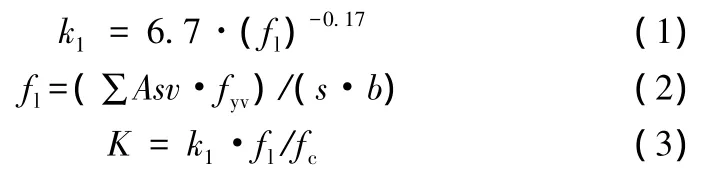
按照约束后的情况，将求得到的相对受压区高度数值再代入《规范》6.2.10－1式后，即可求出承载力与面积配箍率之间的表达式。它们之间的关系曲线如下图示。

图2 梁承载力与配箍量的关系

图2说明，在一定取值范围内，承载力与配箍率之间几乎呈线性增长的关系。

1.2 承载力与纵筋配筋率的关系

如图3所示，赠配钢筋后，在荷载不变的前提下，受力钢筋的应变减小。根据平截面假设，受压区高度将增加到x0。

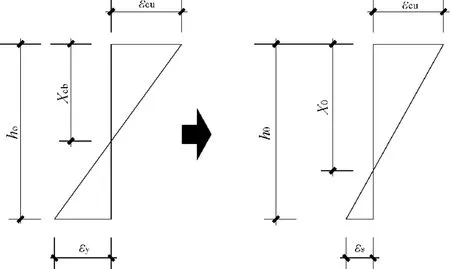
图3 梁正截面应变示意

根据变形协调及相关公式。通过求解，可得出承载力M与纵筋配筋面积AS间的关系。如图4所示:

图4 梁承载力与纵筋配筋率的关系

图4中，梁A受压区配箍率最大，B梁次之，C梁最小。图4说明，增大纵筋配筋率，梁的承载力得到提高。但一定数值以后，曲线趋于平缓。

1.3 刚度分析

可利用以下方法分析梁的刚度变化。

(1)有效惯性矩法。

根据有效惯性矩法(计算方法可参见文献[5])，可推导出梁刚度与配筋率之间的关系。从推导结果可以发现:截面刚度随配筋率的增大而增大，但超过一定数值后，配筋率对刚度变化的影响不再显著。

(2)刚度解析法。

我国现行《规范》中受弯构件短期刚度计算公式是由刚度解析法推导而来，解析方法见《规范》7.2.3节。从中同样也能发现，配筋率的提高可以提升梁的刚度。

2 两种梁的试验研究及对比分析

前期，已进行了3 根约束混凝土梁(B－1、B－2、B－3)与 1根普通混凝土梁(N－1)的受弯试验。试件混凝土均为C30，纵筋均为HRB335，箍筋均为HPB235，设计见表1。

表1 试件设计

试验测得的承载力结果见表2。

表2 极限承载力理论计算值与实测值比较

表2中，N1为按规范计算的理论值，N2为计入箍筋影响后的理论值，F为试验实测值。表2说明约束混凝土梁与普通混凝土梁相比，其承载力有较大幅提升。本次试验的其他结果还表明约束混凝土梁的刚度及延性也有提升。篇幅有限，便不一一例举。

3 预应力约束混凝土梁的非线性有限元模拟分析

现利用有限元软件对约束混凝土梁B－1、预应力约束混凝土梁Y－1进行模拟分析。B－1试件信息见前文，梁Y－1材料与梁B－1相同，截面设计见图5。

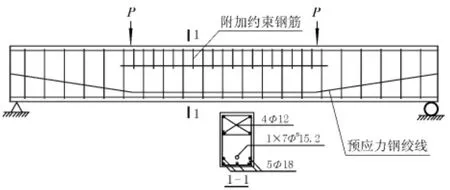
图5 预应力约束混凝土梁截面设计

利用ANSYS软件进行模拟分析。采用分离式模型，混凝土单元采用SOLID65单元，混凝土的本构关系见文献[7]，混凝土的破坏准则为 William-Warnke五参数强度模型[5]。钢筋单元采用LINK8单元，钢筋的本构关系采用双线性各向同性模型。参照文献[8]的方法，建立预应力。假定混凝土和钢筋之间整体性好，不考虑粘结滑移。采用文献[9]的建议，设置以下参数:关闭混凝土的压碎选项;裂缝剪力传递系数取为0.5;本次分析用力的控制加载，收敛准则采用残余力的2范数;收敛标准为0.05，以提高收敛速度;采用修正的Newton-Raphson法求解。

分析结果列于图6。图6中:曲线1是B－1梁试验数据;曲线2是梁B－1的模拟结果;曲线3是梁Y－1的模拟结果。

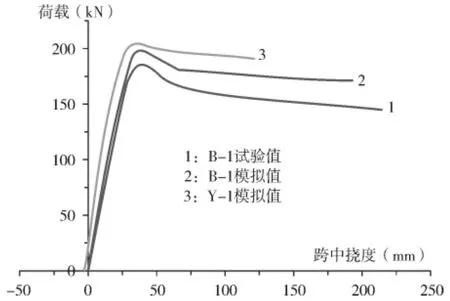
图6 梁荷载-位移曲线

对于B－1梁，试验曲线1和模拟曲线2之间存在一些偏差，原因主要分析假设条件与实际有出入。模拟结果和实际有出入，但仍具有一定指导意义。

曲线3和曲线2相比较说明预应力约束混凝土梁Y－1的承载力略高于约束混凝土梁B－1，而跨中挠度也有所减小。

通过图7可以看出，施加预应力后，混凝土梁的裂缝开展得到有效抑制，进一步说明施加预应力以后构件的性能有所提升。

图7 梁裂缝开展图(B－1左、Y－1右)

4 结论

(1)梁中的箍筋若能采取一定的构造措施，将对其间的混凝土产生有效约束，改善混凝土力学性能，提高构件的延性。

(2)受压区混凝土成为约束混凝土后，混凝土的极限强度和极限应变将会有所提升，此时可在受拉区配置更多的受拉钢筋以提升承载力;因此，推荐使用更高的配筋率以充分发挥构件性能。

(3)对约束混凝土梁施加预应力后，能充分发挥预应力结构和约束混凝土的优势，进一步提高构件性能。

本文存在一定的局限性和不足，针对预应力约束混凝土梁这一全新课题有待进一步研究。感谢贵州大学研究生创新基金(理工2012010)对本课题的资助。

[1]GB 50010－2010混凝土结构设计规范[S]

[2]曹新明.约束混凝土在梁中的应用探讨[J].贵州工业大学学报(自然科学版)，2003，32(1):68－74

[3]Murat Saatcioglu.Strength and Ductility of Confined Concrete[J].Journal of Structural Engineering，1992，118(6):1590－1607

[4]胡海涛，叶知满.复合方箍约束混凝土轴心受压短柱承载力计算[J]. 建筑结构，2002，32(5):13－51

[5]过镇海，时旭东.钢筋混凝土原理和分析[M].北京:清华大学出版社，2003

[6]曹新明.区域约束混凝土浅析[J].工程抗震与加固改造，2008，30(5):112－115

[7]司炳君，孙治国，艾庆.Solid65单元在混凝土结构有限元分析中的应用[J]. 工业建筑，2007，37(1):87－92

[8]刘小燕.预应力高强混凝土梁极限承载力分析[J].中国公路学报，2006，19(1):58－79