5MW风力机叶片弯扭耦合特性分析

赵鹤翔，安利强，周邢银，王璋奇

(华北电力大学 能源动力与机械工程学院，河北 保定071003)

0 引 言

风力机在运行过程中受到复杂的载荷作用，特别是疲劳载荷。风力机叶片运行的20 ～30a，疲劳载荷将超过108个循环。对于MW 级叶片，减少疲劳载荷是很重要的。很多方法可以用于降低叶片的疲劳载荷，比如采用先进的复合材料、利用各向异性复合材料的弯扭耦合特性等。由于复合材料具有各向异性特性，因此叶片在承受纯弯曲载荷时发生扭转。弯曲载荷的增加将导致扭角的增大，使得气动载荷降低。文献［1 ～3］指出足够的弯扭耦合可以降低将近10 %的疲劳载荷。

国内外很多学者对风力机叶片的弯扭耦合特性进行了大量研究。文献［4］研究了叶片主梁简化模型即，等截面D 型梁的铺层材料、铺层方式、内部筋板等因素对弯扭耦合性能的影响，得出铺层材料、铺层角度及铺层厚度比是影响弯扭耦合最主要的因素。文献［5 ～8］研究了不同功率等级叶片的主梁材料及铺层角度对弯扭耦合系数的影响规律。以上文献的研究中均没有考虑叶片内部结构的不同对弯扭耦合性能的影响。文献［9］对叶片不同的主梁型式分别进行了弯扭耦合特性研究，指出等截面C 型主梁弯扭耦合效应最明显，但该文献没有研究弯扭耦合特性沿展向的分布特性，且没有研究真实叶片内部结构的变化对整个叶片弯扭耦合特性的研究。

本文采用三维有限元方法建立NREL 5 MW叶片模型，给出了叶片弯扭耦合特性计算方法，研究叶片梁帽铺层材料和叶片内部结构型式对叶片弯扭耦合特性的影响规律，为进一步研究应用复合材料叶片弯扭耦合特性降低叶片气动疲劳荷载提供依据。

1 弯扭耦合系数定义

由薄壁应力与截面反力的静平衡方程得到弯矩M、扭矩T，弯曲率Kx和扭曲率φz之间的关系式［10］:

式中:EI 为弯曲刚度;GJ 为扭转刚度;β 是用于描述耦合程度的系数:

式中:θ 为挥舞方向的角度;φ 为扭转角度;x 为轴向。

当叶片只受到纯弯曲载荷，即T=0，代入到式(1)，得到:

式中:Kx和φz的取值由有限元分析结果得到［11］。

2 有限元模型

叶片常见的腹板型式通常有两种，箱型和双槽型，如图1 所示。

本文建立的NREL 5 MW 风力机叶片模型数据来源于NREL 实验室的公开资料［12］，该叶片已被广泛应用风力机叶片的研究。5 MW 叶片由蒙皮、梁帽和腹板组成。蒙皮、腹板通常采用三明治结构。蒙皮、梁帽由胶衣、表面毡、玻璃纤维单向布、双向布组成。表1 给出了5 MW 叶片所用复合材料的力学特性［13］。

图1 叶片截面典型结构Fig.1 Typical cross section of blade

NREL 5 MW 叶片长度为61.5 m，由7 种不同的翼型组成，在20 %附近的位置达到最大弦长，为4.8 m。表2 给出了5 MW 叶片各截面翼型、弦长、扭角等信息。其中0 ～6.8 %为叶根区域，6.8% ～13.5 %为过渡区域，13.5 % ～100 %为气动翼型区域。

表1.铺层材料特性Table 1 Layer material properties

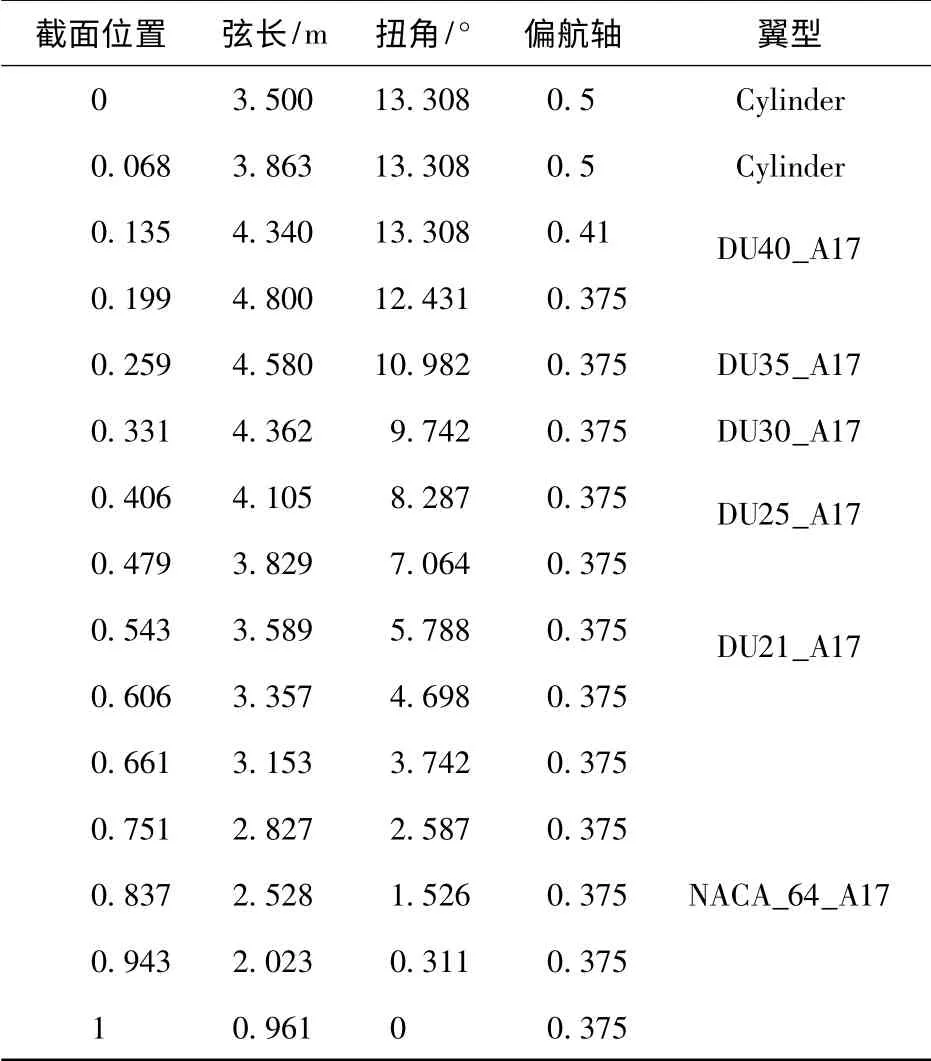
表2 5MW叶片翼型和弦长特性Table 2 5 MW blade airfoil and chord properties

用ANSYS 软件建立叶片的有限元模型如图2所示，叶根部位采用固定端约束。采用SHELL99单元对叶片进行剖分，共计3 168 个单元和9 406个节点。SHELL99 单元的更多信息见文献［14］。

图2 5 MW 叶片有限元模型( 带有边界条件)Fig.2 ANSYS finite element model of the 5MW blade( with boundary conditions)

图3 给出了叶片最大弦长处梁帽的铺层序列，其中三向布由双向布和单向布组成。

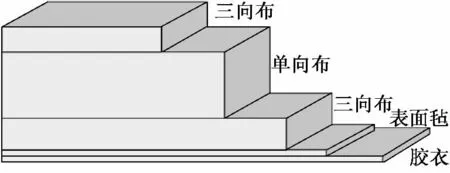
图3 梁帽铺层序列Fig.3 Layer stacking sequence of spar cap

3 5 MW 叶片弯扭耦合特性分析

大型叶片常用的材料为玻璃纤维和碳纤维，但由于碳纤维昂贵的价格，因此目前叶片设计仅用于叶片梁帽铺层。本文分别选用玻璃纤维和碳纤维作为叶片梁帽的铺层材料，其余部位均采用玻璃纤维，建立了4 种不同的叶片模型来研究影响叶片弯扭耦合特性的因素，各叶片模型材料及内部结构如表3 所示。在每种模型研究中，在叶尖都施加了2 个20 000 N 的集中载荷，如图2所示。

表3 不同叶片模型的材料及内部结构Table 3 Material and internal structure of different blades

3.1 铺层角度的影响

建立叶片模型1，该叶片全部由玻璃纤维制造，叶片内部结构采用图1(a)所示的箱型。改变梁帽的单向布铺层角度，从0°变化到40 °，得到的叶片挥舞方向弯曲角如图4 所示。

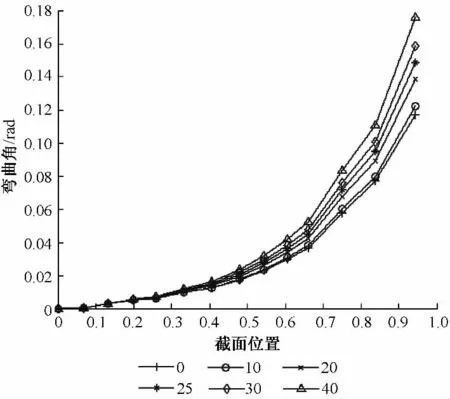
图4 模型一挥舞方向弯曲角Fig.4 Flapwise bending angle of the first model

从图4 可以看出，从叶根到叶尖，对于同一铺层角度叶片，截面弯曲角度呈二次曲线规律增大;在相同的截面位置处，随着梁帽铺层角度的增加，挥舞方向的弯曲角度也逐渐增大。这说明随着铺层角度偏离叶片轴向越大，叶片挥舞方向弯曲刚度越小，使得弯曲变形角度增大。

模型一的扭转角如图5 所示。

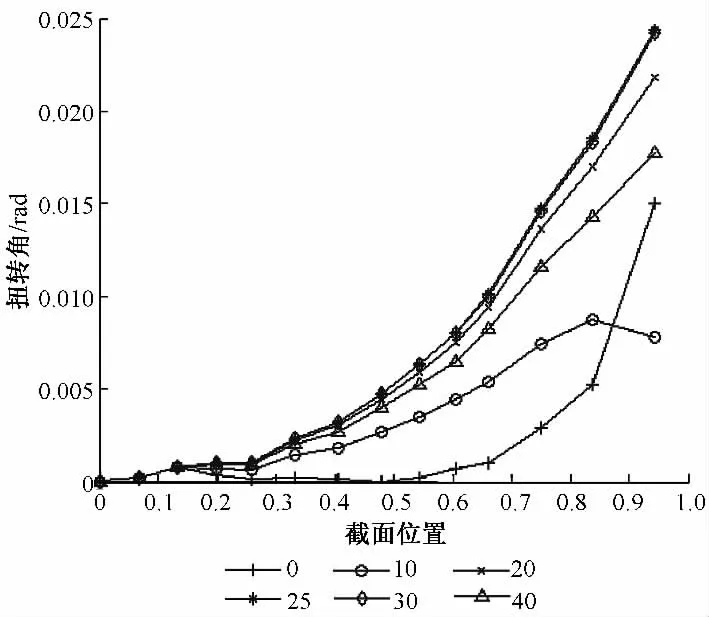
图5 模型一扭转角Fig.5 Twist angle of the first model

从图5 中可以看出，从叶片根部到叶尖部位，对于同一铺层角度叶片，截面扭转角度逐渐增大;而在相同的截面位置处，随着梁帽铺层角度的增加，挥舞方向的扭转角度出现先增大后减小的变化规律，在25 ～30°范围达到最大值。

模型一的弯扭耦合系数的分布如图6 所示。

图6 模型一耦合系数βFig.6 Coupling efficient of the first model

图6 中可以看出，从叶片根部到叶尖部位，同一铺层叶片的弯扭耦合系数基本呈现出先增大后减小的趋势。在同一截面位置处，耦合系数随着铺层角度的增大，也是先增大后减小。在25 °铺层角度时能获得最大的弯扭耦合系数，铺层角度为20 °时，其弯扭耦合系数只是略低于最大值，此结论与文献［7］相符。

3.2 材料类型对弯扭耦合特性的影响

取梁帽玻璃纤维铺层角度为25 °，叶片内部结构为箱型，建立叶片模型2。保持铺层角度和内部结构不变，将梁帽的玻璃纤维替换为铺层角度为25 °的碳纤维，建立复合铺层叶片模型3。计算得到两个模型的耦合系数如图7 所示。从图7 中可以看出，在同样的铺层角度下，模型3 比模型2 的耦合程度更大，将近1 倍关系。

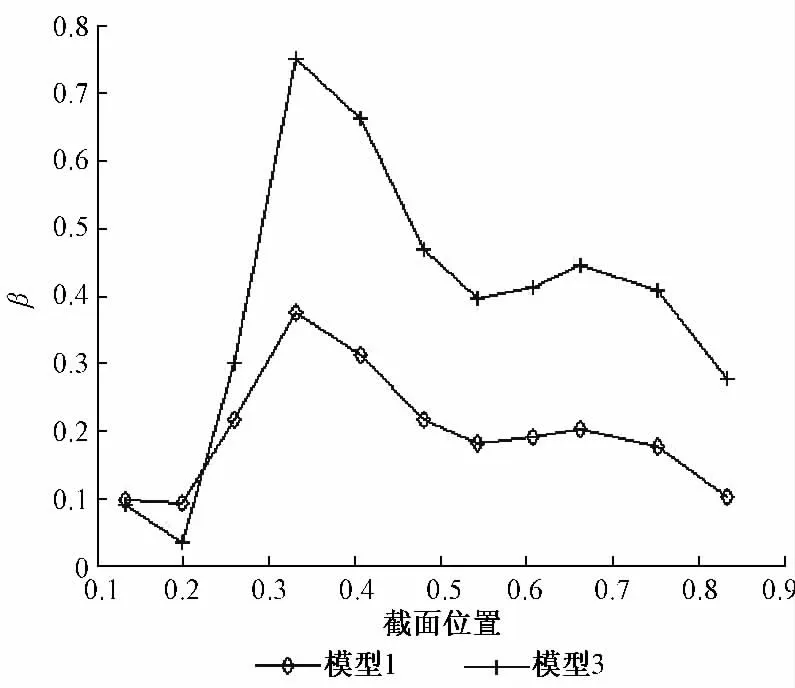
图7 模型2，3 耦合系数βFig.7 Coupling efficient of the second and three models

3.3 主梁结构对弯扭耦合特性的影响

采用25°铺层的碳纤维梁帽铺层，建立内部结构为双槽型的叶片模型4。在同样的载荷下，计算得到的弯曲角度、扭转角度和耦合系数分别如图8至图10 所示。

图8 模型4 挥舞方向弯曲角Fig.8 Flapwise bending angle of the fourth model

图9 模型4 扭转角Fig.9 Twist angle of the fourth model

图10 模型4 耦合系数βFig.10 Coupling efficient of the fourth model

从图8 至图10 中可以看出，沿叶片展向，挥舞方向弯曲角、扭转角和耦合系数具有与前3 种模型相似的分布规律，即靠近叶尖的位置各角度逐渐增大。但是，内部结构为双槽型的叶片其耦合系数明显大于内部结构为箱型的叶片耦合系数，可见内部结构也是影响耦合系数的关键因素之一。

4 结 论

本文采用有限元方法分析了5 MW 叶片的弯扭耦合特性。讨论了玻璃纤维不同铺层角度、材料类型、内部结构型式等对弯扭耦合特性的影响规律，得到如下结论:

(1)铺层角度是影响叶片弯扭耦合性能的重要因素。对于玻璃纤维叶片，获得最大弯扭耦合效应的角度为20 ～30°。

(2)材料是影响耦合特性的重要因素。在同样铺层角度下，碳纤维能够获得比玻璃纤维更显著的弯扭耦合效应。

(3)主梁的结构型式对叶片弯扭耦合程度影响很大。不同结构型式的主梁，其弯扭耦合效应是不同的，双槽型主梁具有比箱型主梁更明显的弯扭耦合效应。

［1］Lobitz D W，Laino D J.Load mitigation with twist-coupled HAWT blades ［C］.Reno:ASME Wind Energy Symposium，1999，124 －134.

［2］Lobitz D，Veers P，Laino D，Performance of twist-coupled blades on variable speed rotors ［C］.Reno:ASME Wind Energy Symposium.2000，43 －52.

［3］Lobitz D W，Veers P S，Eisler G R，et al.The use of twist-coupled blades to enhance the performance of horizontal axis wind turbines ［R］.Albuquerque:Sandia National Laboratories，2001，10 －14.

［4］Ong C H，Tsai S W，Design，manufacture and testing of a bend-twist D-Spar ［R］.Albuquerque:Sandia National Laboratories，1999.

［5］李军向.大型风机叶片气动性能计算与结构设计研究［D］.武汉:武汉理工大学，2008.

［6］刘旺玉，张勇.柔性风力机叶片主梁弯扭耦合设计［J］.华南理工大学学报(自然科学版)，2012，38 (12):1 －6.

［7］Locke J，Ulyses Valencia.Design studies for twist-coupled wind turbine blades ［R］.Albuquerque:Sandia National Laboratories，2004.

［8］Dayton Griffin.Evaluation of design concepts for adaptive wind turbine blades ［R］.Albuquerque:Sandia National Laboratories，2002.

［9］Walsh J W.Composite material bendtwist couplng for wind turbine blade apllications ［D］.Laramie Wyoming University，2009.

［10］Locke J E，Contreras I.The implementation of braided composite materials in the design of a bend-twist coupled blad ［R］.Albuquerque:Sandia National Laboratories，2002.

［11］McKittrick L R，Cairns D S，Mandell J，et al.Analysis of a composite blade design for the AOC 10/50 wind turbine using a finite element model ［R］.Albuquerque:Sandia National Laboratories，2001.

［12］Jonkman J，Butterfield S，Musial W，et al.Definition of a 5 －MW reference wind turbine for offshore system development ［R］.Golden CO:National Renewable Energy Laboratory，2009.

［13］Zhou Xingyin，An Liqiang，Wang Zhangqi.Twist-bend coupling analysis for 5 MW wind turbine blades ［J］.Applied Mechanics and Materials，2012，(152－154):703－708.

［14］ANSYS Inc.ANSYS Theory Reference Manual ［EB/OL］.http://www.ansys.com.