汽轮机螺栓应力松弛行为预测的研究

董 瑾

(华北电力大学 数理学院，北京102206)

0 引 言

应力松弛或弹性衰退是各种材料，特别是金属材料在服役时出现的一种物理现象，是各种螺栓、弹簧等零部件的主要失效形式。汽轮机螺栓工作环境恶劣，在运行中受到温度、应力和环境介质的联合作用，紧固螺栓在长期高温和应力的作用下，内部将发生与时间相关的塑性变形，由于总变形恒定，在塑性变形增加的同时，将引起弹性变形量的减少，使压紧力下降。这种在恒定变形条件下，材料内部的变形由弹性向非弹性的转变，引起应力随时间下降的现象就是应力松弛。金属在高温下抵抗松弛的能力是材料重要的高温强度性能指标，在零件的设计中松弛性能是选材依据之一，为了保证设备安全运行，研究金属的应力松弛行为有很重要的意义，而且“应力松弛及弹性衰退”也是材料科学与工程中基础理论研究的一个重要课题。然而，为了获取高温金属材料的应力松弛性能参数，必须进行长时间的松弛试验，因此研究一种普遍的简便可行而不失科学性的高温设计方法来表征应力松弛行为和预测长时剩余应力成为人们关注的焦点［1～3］。

本文以应力松弛的基本特性为基础，依据松弛第一、第二定律，提出一种用以预测应力松弛行为过程的动力学方程式。该数学表达式可以完整地反映出松弛初期和长时间以后的松弛行为，可以准确预测确定出相同温度下、不同初应力时的应力松弛曲线，从而避免了长时的应力松弛试验 (一般需105h)，具有很大的工程实际意义。

1 应力松弛的动力学

1.1 典型应力松弛曲线分析

应力松弛动力学主要研究该过程的速度快慢及松弛到何种程度的影响因素，它对零部件的生产和应用有重要意义。应力松弛的基本机理目前尚不十分清楚，但其应力松弛行为，从典型松弛曲线可以看出通常具有以下基本特征:松弛初期，试样内的剩余应力急剧降低，但随时间增加，松弛速度逐渐减缓;松弛速度随初应力增加而增加，长时间后的不同初应力下的剩余应力将相互接近，并以松弛极限σr为其渐近值，即初应力的大小对剩余应力的影响在松弛初期显著，而对长时间后逐渐减弱［3，4］。

1.2 应力松弛第一、第二定律

在任一时间t，不同初应力σ0和σ′0所对应的应力下降量Δσ 和Δσ′ 之间具有简单的关系，即遵从松弛第一定律［3］:

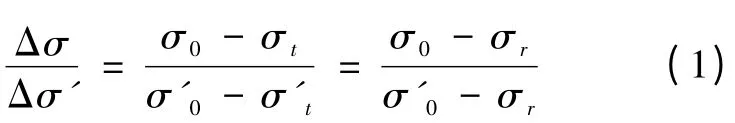
式中:σt和σ′t是所选择时间间隔内的剩余应力，σr为材料的松弛极限。根据这个定律即可由一条松弛曲线作出相同温度下，任何初应力的松弛曲线。

若对所有时间，式 (1)的比例关系保持不变，则初应力为σ0的应力松弛速率νr(即单位时间内应力松弛的幅度和初应力为σ′0的松弛率ν′r一定与Δσ 和Δσ′ 成比例:

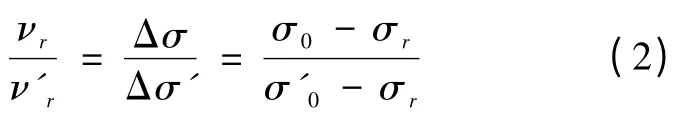
式 (2)称为松弛第二定律。当σr等于零时，式(1)和 (2)变为

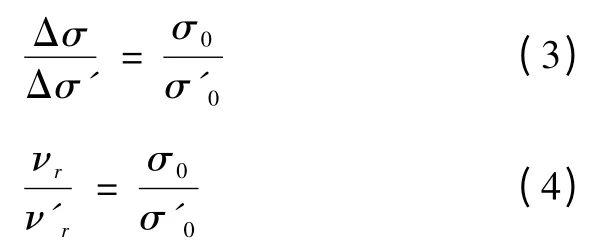
即在任何时间，应力下降量和松弛速率都与初应力成比例。

2 应力松弛动力学方程式的建立

大量金属材料的松弛实验数据绘制的应力松弛曲线和回归分析表明，松弛曲线可用回归方程表示其规律性变化［5，6］:

式中:σ 为松弛t 时间的剩余应力，MPa;a 为该直线方程与纵坐标轴的交点;b 为应力松弛率，即该直线段的斜率;t 为松弛时间，h。

a、b 数值为与材料试验初始应力σ0及试验温度T 有关的常数。由式 (5)可知，从曲线或从回归方程中确定了a、b 值，则任意时间t 下的剩余应力σ 便可确定。上述应力松弛动力学对数方程式，对于松弛Ⅰ、Ⅱ阶段均适用。对于松弛Ⅰ阶段的松弛时间较短，其松弛过程主要体现为第Ⅱ阶段，采用该方程更为方便。

松弛极限σr一般很难得到，因为对于大多数金属材料来讲，其值较小，通常并不直接用松弛极限来评定材料的抗松弛性能。Cr-Mo 钢和Cr-Mo-W 钢研究表明，在经过相当长的实验时间，应力持续明显下降，且仍然看不到松弛的下限应力［4］。

对于汽轮机螺栓Cr-Mo-V 热强钢，当忽略松弛极限时，式 (3)可变为

将式 (5)带入式 (6)，可得:

式 (7)即是借助于松弛的经验公式和松弛第一、二定律本文提出的应力松弛动力学方程式。使用该方程式即可由某初应力下的松弛曲线，通过回归确定各材料常数，来预测相同温度下不同初应力时的松弛行为以及对短时试验结果进行外推。

3 实验结果的拟合及分析

为证明式 (5)和 (7)的合理性与正确性以及是否适用于汽轮机螺栓材料，现利用实验结果进行拟合。图 1 为 20Cr1Mo1VTiB 螺栓钢538 ℃下的应力松弛曲线，图中有初应力309 MPa 和226 MPa 的实验结果［7］。由式 (5)对初应力309 MPa 松弛实验结果进行拟合，通过回归分析确定材料常数a 和b 值分别为320.47 和12.80，从图中可以看出，式 (5)用于松弛行为的描述具有很高的精度，与试验结果吻合良好。然后把a、b 值代入式 (7)，利用该方程式作出初应力226 MPa 的预测曲线，从图中可以看出，与实际的应力松弛试验结果有较好的吻合度，其相对误差小于3 % ～5 %。

图2 为25Cr2Mo1V 钢550℃下的应力松弛曲线，用前述方法首先对初应力400 MPa 实验结果［7］进行 拟 合，a、b 值 分 别 为363.66 和32.67，尔后作出初应力300 MPa 的预测曲线。由于松弛初期实验数据点比较分散，拟合和预测曲线与数据点有一定偏离，但与松弛一定时间后的结果吻合较好。经过与大量的Cr-Mo-V 汽轮机螺栓耐热钢的应力松弛实验结果进行比较，均得到了良好的拟合结果，拟合精度较高，由此可以推断本文提出的应力松弛动力学方程式的适用性，可以利用式 (5)和 (7)表达式对材料的松弛性能进行分析。同时该表达式形式简单，易于拟合，并且可以方便地计算不同初应力时的剩余应力，便于工程应用。

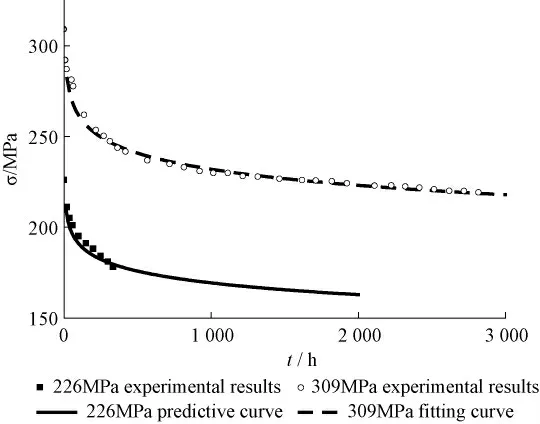
图1 20Cr1Mo1VTiB 螺栓钢的应力松弛曲线(538℃)Fig.1 Stress relaxation curves of 20Cr1Mo1VTiB bolt steel (538℃)

4 松弛性能分析及讨论

4.1 不同初应力的松弛塑性应变速率与时间的关系

一般认为，金属零件中产生应力松弛主要是在总变形不变的条件下，一部份弹性变形转变成塑性变形致使弹性力减小，弹性变形的减小与塑性变形的增加是同时等量进行的，在弹性范围内加载时，应力松弛过程可以表示为

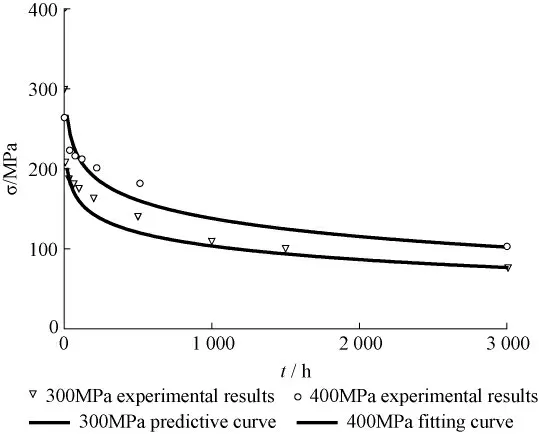
图2 25Cr2Mo1V 螺栓钢的应力松弛曲线 (550℃)Fig.2 Stress relaxation curves of 25Cr2Mo1V bolt steel(550℃)

式中，ε0为总变形，εe为弹性变形，εp为塑性变形。若设εe= σ/E，E 为材料弹性模量，上式两边对时间求导数，则得:

将式 (7)对时间求导数，并代入式 (9)可得:

式 (7)表明塑性变形速率与初应力和时间有关，在此，不同初应力条件下的应力松弛速率的关系满足松弛第二定律。根据式 (10)可确定在不同的初应力下，20Cr1Mo1VTiB 螺栓钢538 ℃下的塑性变形速率与时间的关系曲线，如图3 所示。从图中可以看出，在加载后较短的时间内，ε·p 急剧下降;相同的松弛时间，高初应力的ε·p 要比低应力的变形速率大，即ε·p 与总应变的大小有关;当松弛一定时间后，由于材料的应变硬化，塑性变形速率的下降速度逐渐变缓，并且逐渐趋于相近，即不同初应力下的ε·p 几乎与初应力的大小无关;同时ε·

p 的变化有趋于恒定值的趋势，说明剩余应力逐渐与松弛极限接近。

值得注意的是，在相同剩余应力条件下，初应力越大，松弛应变速率越大，变形总量也越大(σ = σo- Eεp)，由于累积塑性应变越大，因而造成的应变硬化效果也越显著，同时造成的材料塑性损伤也越大，这就要求在工程应用时，在满足剩余应力的前提下，不能无限提高初应力的水平。

图3 20Cr1Mo1VTiB 钢的关系曲线(538℃)Fig.3 curves of 20Cr1Mo1VTiB bolt steel(538℃)

4.2 不同初应力的塑性应变速率与剩余应力的关系

由式 (5)可得:

将式 (11)代入式 (10)得:

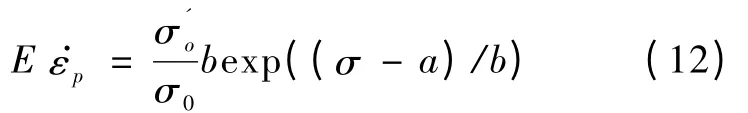
式 (12)表明，ε·p 是σo和σ 的函数。

一般在研究应力松弛时认为，第二阶段应力下降速度逐渐减缓，当忽略松弛极限σr时，剩余应力σ 可用经验公式计算［3］，其经验公式为

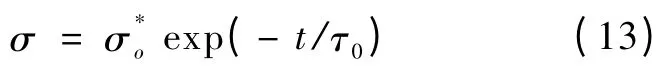
式中的σ*o 和τo分别为第二阶段假定初始应力和材料常数。由该式可得到塑性应变速率的计算式为

由于认为τo为常数，得到的ε·p 由σ 唯一确定，并成线性关系。文献［4］的测试结果表明还应与σ0有关，而按式 (13)，显然无法正确得到松弛应变速率

5 结 论

(1)以应力松弛的基本特性为基础，依据松弛第一、第二定律，提出了一种用以描述松弛全过程的应力松弛动力学方程式。多种螺栓材料Cr-Mo-V 钢的试验数据拟合结果表明，该数学表达式可以完整地反映松弛行为，适应性强，拟合精度较高，并且形式简单，便于工程应用。

(2)该方程式能够以一种初应力下的应力松弛曲线为基础，来准确预测确定出相同温度下、不同初应力时的应力松弛曲线，能方便地进行不同初应力条件下的剩余应力的预估，从而避免了长时的应力松弛试验 (一般需105h)，具有很大的工程实际意义。

(3)利用E ε·p～t 关系曲线，研究了不同初应力松弛塑性应变速率随时间的变化及其趋势比较，其规律与现有的研究结果一致。由应力松弛动力学方程式导出的松弛应变速率ε·p是初应力σo和剩余应力σ 的函数，这也与实验研究相吻合。

［1］郭进全，轩福贞，何磊.螺栓材料1Cr10NiMoW2VNbN的应力松弛行为及预测模型［J］.核动力工程，2008，29 (6):119 -124.

［2］金尧，戴振羽，高庆.40CrNi2MoV 钢应力松弛特性研究［J］.核动力工程，1999，20 (1):21 -24.

［3］杨宜科，吴天禄，江先美，等.金属高温强度及试验.上海:上海科技出版社，198.

［4］平修二.金属材料的高温强度理论与设计［M］.北京:科学出版社，1983.

［5］Margaret O′Molley Bsc.Stress Relaxation of Springs［J］.Wire Industry，1988，12:808 -813.

［6］苏德达.弹簧 (材料)应力松弛及预防［M］.天津:天津大学出版社，2002.

［7］姜求志，王金瑞.火力发电厂金属材料手册［M］.北京:中国电力出版社，2001.