恒温下结构钢的应力－应变关系

李毅，王志滨

(福州大学土木工程学院，福建福州 350116)

0 引言

恒温加载试验比较容易控制，可直接得到不同高温下的单向拉伸应力－应变关系全曲线，所以钢材高温材性试验大多采用恒温加载试验，许多国家颁布实施的金属高温特性试验标准和钢结构抗火设计规范也主要基于恒温加载试验［1］.李国强［2］、Kelly和Sha［3］通过恒温加载试验对高温中钢材的重要力学性能指标进行了测定.赵金城［4］、Hu［5］、Qiang［6］不仅实测了高温中钢材的力学性能指标，而且给出了钢材在不同高温下应力 － 应变关系的实测曲线.Outinen 和 Mäkeläinen［7］、Outinen［8］、Schneider和 Lange［9］、Poh［10］也分别给出了不同强度钢材在恒温加载条件下的应力 －应变关系实测曲线;其中Poh［10］还对ASCE［11］和EC3［12］中的钢材高温应力－应变关系模型进行了对比分析.本研究在上述试验研究的基础上，通过对恒温加载试验曲线的回归分析，提出高温中钢材的应力－应变关系模型.

1 高温中钢材的力学性能

图1为高温中钢材典型的应力－应变关系曲线［5］，从图1可以看出:随着温度的升高，应力－应变关系曲线的形状发生显著变化;200℃ 以内，应力－应变关系曲线有明显的屈服平台，屈服强度有小幅度降低，极限强度差别不大;300℃ 左右，屈服强度明显降低，屈服平台也变得越来越小，极限强度下降不大;400℃ 以后，应力－应变关系曲线已无屈服平台，极限强度急剧降低;800℃ 以后，钢材基本丧失承载能力.由此可见，常温下的钢材应力－应变关系曲线有明显的弹性段、屈服平台段和应变硬化段，随着温度的升高，屈服平台段逐渐消失，钢材应力－应变关系曲线从弹性段直接进入到应变硬化段.因此，本文提出了恒温下结构钢的应力－应变关系曲线简化模型，如图2所示.

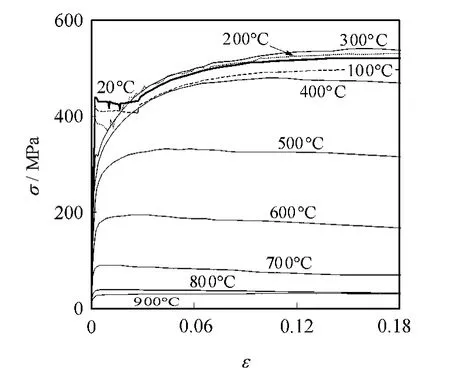
图1 高温中钢材典型的应力－应变关系曲线Fig.1 Typical stress－ strain curves

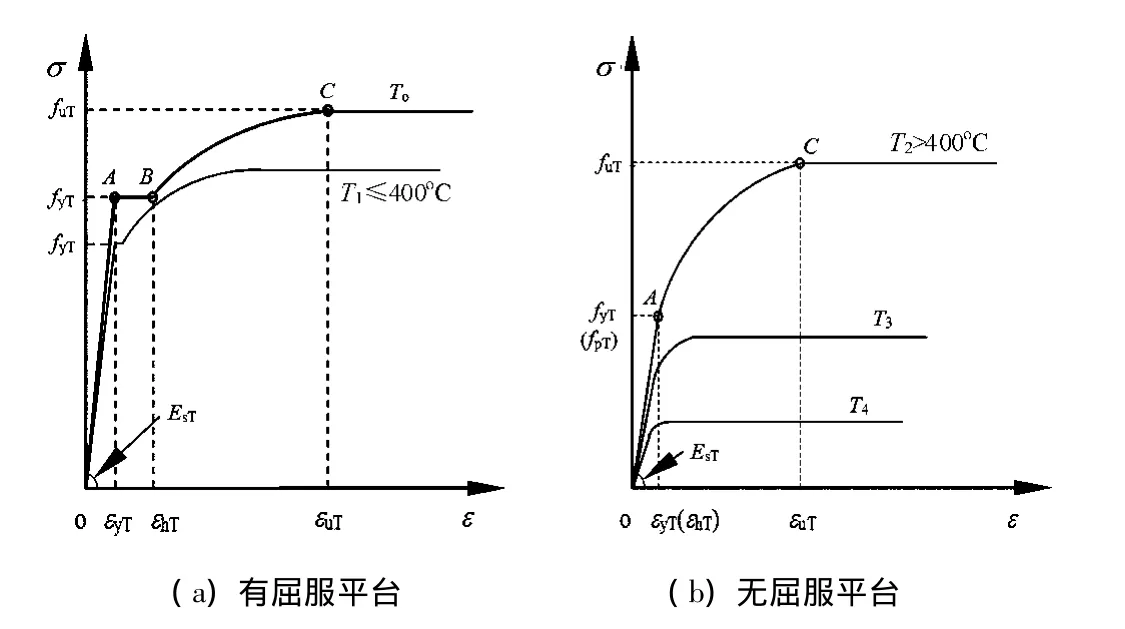
图2 高温中钢材的应力－应变关系模型Fig.2 Stress－strain model at elevated temperatures

图3为高温中钢材重要的力学性能指标随温度变化的情况，图中Es、fy和fu分别为常温下钢材的弹性模量、屈服强度、极限强度，EsT、fyT和fuT分别对应为高温中的各力学性能指标.图3(b)中需要特别说明:有明显屈服平台的应力－应变关系曲线取其屈服平台的下屈服点作为屈服强度;没有屈服平台则取其比例极限作为屈服强度;这样的定义有利于分析比较不同高温下应力－应变关系曲线上“关键点”的变化规律.

图3 高温中钢材力学性能与温度的关系Fig.3 EsT、fyTand fuTas a function of temperature

从图3看出:在所收集的数据中，不同强度钢材的弹性模量、屈服强度和极限强度在高温中的变化趋势基本一致;弹性模量在300℃ 以内变化不大，300℃ 时只降低到常温下的95%左右，300℃ 以后，随着温度的升高，弹性模量开始出现显著降低;屈服强度在200℃ 时降低到了常温下的92%左右，200℃ 以后开始出现显著降低;极限强度在400℃ 以内变化不大，400℃ 时降低到常温下的89%左右，400℃ 以后开始出现急剧下降;在进入800℃ 左右的高温后，弹性模量、屈服强度和极限强度的变化随温度的升高开始趋于平缓;1000℃ 时，弹性模量、屈服强度和极限强度分别只剩下常温下的18%、3.2%和4.8%.由此可见，弹性模量、屈服强度和极限强度随温度变化的总体趋势基本一致，下降幅度由小到大再趋于平缓，这就为采用统一表达式来拟合高温中的弹性模量、屈服强度和极限强度提供依据.

2 钢材的应力－应变关系模型

采用图2中所示的简化曲线对实测的应力－应变关系曲线进行拟合:对于有屈服平台的情况，分为弹性段(OA)、屈服段(AB)、应变硬化段(BC)和极限强度段(C点以后)，如图2(a);随着温度的升高，逐渐过渡到图2(b)所示三段线形式;因此只要确定A、B和C三个“关键点”的合理取值，即可求得简化的全曲线.

2.1 应力－应变关系表达式

对于图2中所示的应力－应变关系模型，其数学表达式如下:

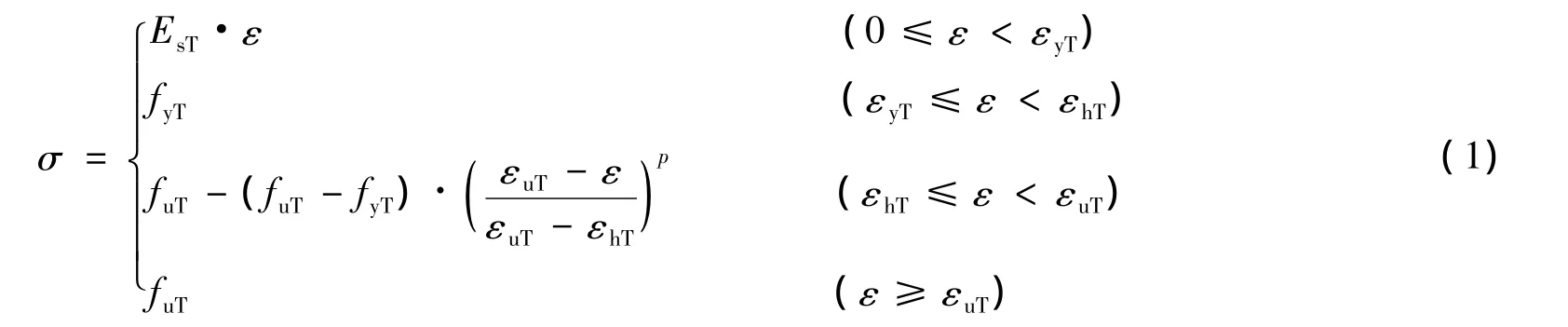
其中:εyT、εhT、εuT分别为高温中钢材的屈服应变、硬化应变、极限应变，εyT=fyT/EsT;p为应变硬化段的硬化参数;T为升温阶段的当前温度(℃ ).为了确定式(1)的具体表达式，需要对图2中的各参数进行计算.

2.2 弹性模量EsT

对图3(a)中的实测数据进行拟合，得到高温中弹性模量随温度变化的计算公式如下:

2.3 屈服强度fyT和极限强度fuT

对图3(b)、(c)中的实测数据进行拟合，得到高温中屈服强度和极限强度随温度变化的计算公式如下:

图4为常温下钢材极限强度和屈服强度的比值fu/fy与屈服强度fy之间的关系，由图4可见，极限强度fu可用屈服强度fy来表示，见式(5).

图4 常温下fu/fy与fy的关系Fig.4 Ratio of fu/fyas a function of fy

图5 硬化应变与温度、屈服强度的变化关系Fig.5 εhTas a function of T and fy

2.4 硬化应变εhT和极限应变εuT

由图5得高温中硬化应变与屈服应变的比值随温度变化、以及常温下硬化应变与屈服应变的比值随屈服强度变化的计算公式如下:

所以，由式(6)和式(7)可得高温中硬化应变的最终计算公式如下:

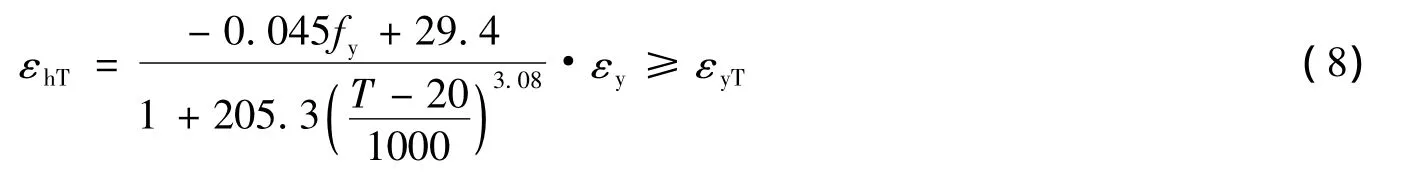
由图6得高温中极限应变与屈服应变的比值随温度变化、以及常温下极限应变与屈服应变的比值随屈服强度变化的计算公式如下:

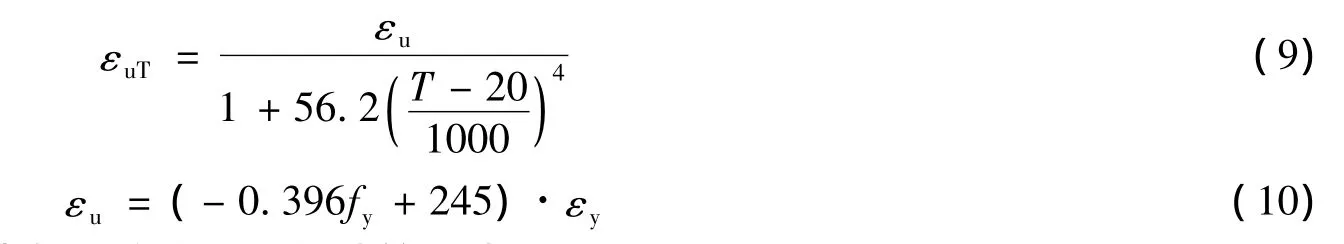
所以，由式(9)和式(10)可得高温中极限应变的最终计算公式如下:

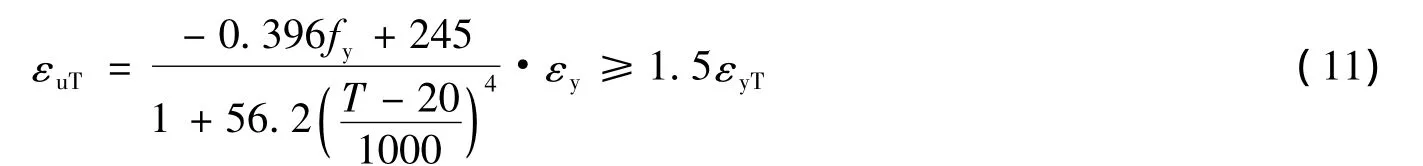
2.5 硬化参数p

由图7中的数据点拟合得硬化参数随温度的变化的计算公式如下:

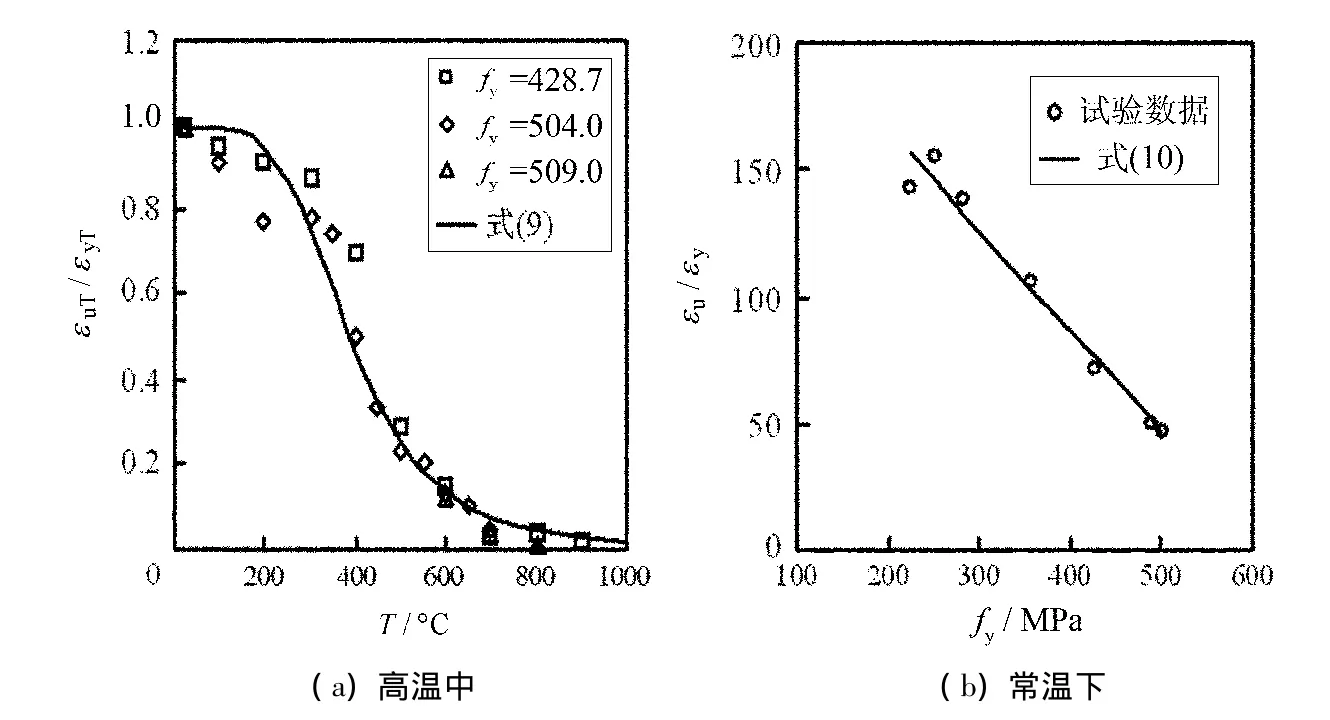
图6 极限应变与温度、屈服强度的变化关系Fig.6 εuTas a function of T and fy

图7 硬化参数与温度的关系Fig.7 p as a function of T

3 计算曲线与实测曲线比较

由于篇幅所限，图8中列出了部分高温中钢材应力－应变关系的计算曲线与试验曲线的比较.由图8可见，与ASCE模型［11］、EC3模型［12］相比，高温中钢材应力－应变关系模型与实测曲线吻合度更好.

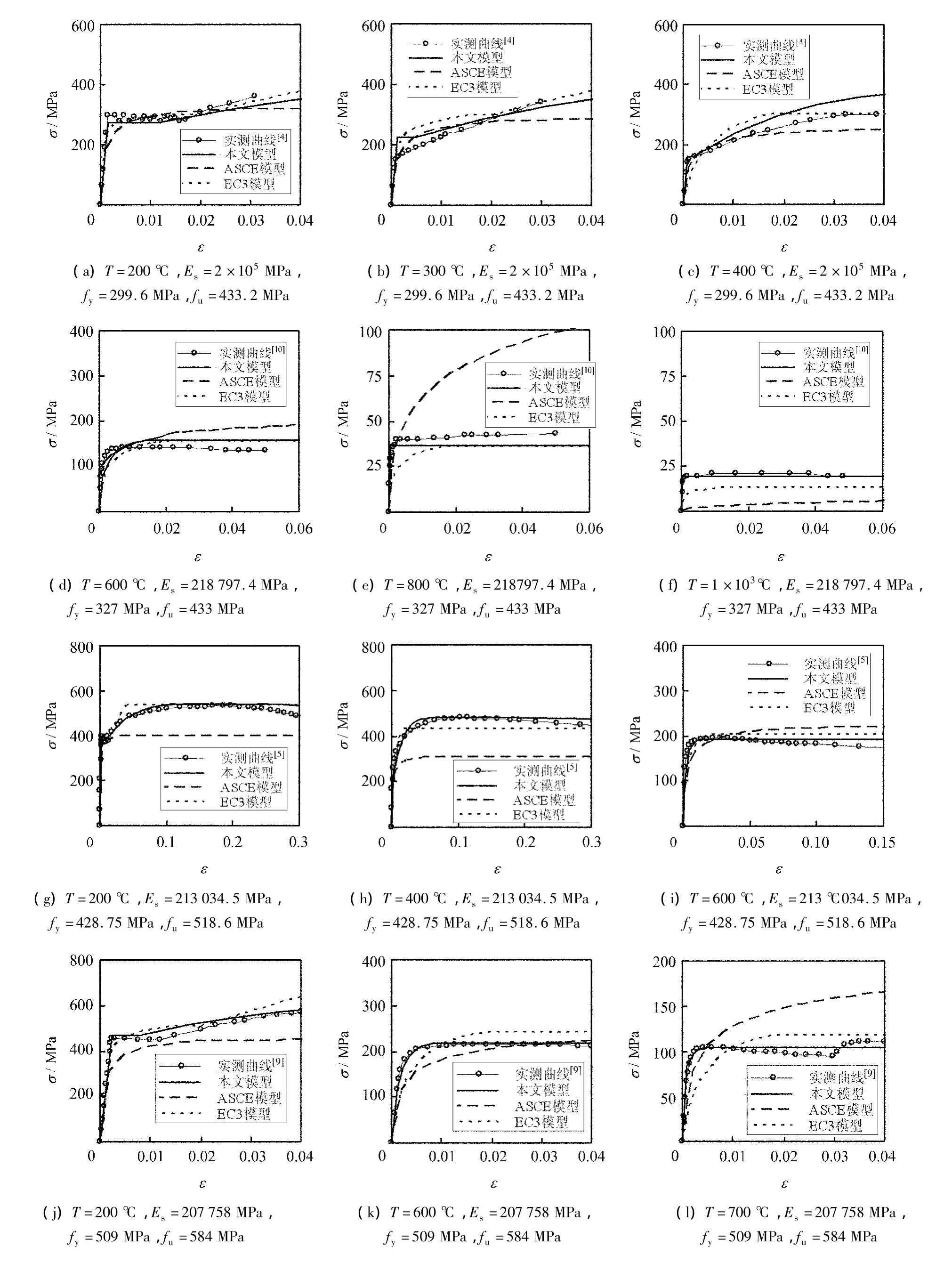
图8 实测应力－应变曲线与计算曲线的比较Fig.8 Comparison between stress－ strain relation model and test curves

4 结语

提出高温中钢材应力－应变关系模型.通过该模型，只需常温下钢材的屈服强度(fy)和温度(T)，就可以求出某一温度下钢材的应力－应变关系全曲线，可方便地应用于结构抗火性能的数值分析中.该模型的适用范围为:fy=200～500 MPa、T=20～1 000℃，常温下钢材的弹性模量(Es)统一取为2.06×105MPa.

［1］李国强，韩林海，楼国彪，等.钢结构及钢－混凝土组合结构抗火设计［M］.北京:中国建筑工业出版社，2006.

［2］李国强，张晓进，蒋首超，等.高温下SM41钢的材料性能试验研究［J］.工业建筑，2001，31(6):57－59.

［3］Kelly F S，Sha W.A comparison of the mechanical properties of fire－resistant and S275 structural steels［J］.Journal of Constructional Steel Research，1999，50(3):223－233.

［4］赵金城.高温下钢材力学性能的试验研究［J］.建筑结构，2000，30(4):26－28.

［5］Hu G，Morovat M，Lee J，et al.Elevated temperature properties of ASTM A992 steel［C］//Proceedings of Structures Congress 2009:Don’t Mess with Structural Engineers:Expanding Our Role.Austin:［s.n.］，2009:1 －10.

［6］Qiang X H，Bijlaardb F S K，Kolsteinb H.Elevated－temperature mechanical properties of high strength structural steel S460N Experimental study and recommendations for fire－resistance design［J］.Fire Safety Journal，2013，55(1):15 －21.

［7］Schneider R，Lange J.Constitutive equations of structural steel S460 at high temperatures［C］//Proceedings of Nordic Steel Construction Conference.Darmstadt:［s.n.］，2009:204 －211.

［8］Poh K W.Stress－strain－temperature relationship for structural steel［J］.Journal of Materials in Civil Engineering，2001，13(5):371－379.

［9］Outinen J，Mäkeläinen P.Transient state tensile test results of structural steel S355(RAEX 37 －52)at elevated temperatures［J］.Journal of Structural Mechanics，1994，28(1):3 －18.

［10］Outinen J，Jyrki Kesti，Mäkeläinen P.Behavior of high － strength structural steel S420M at elevated temperatures［J］.Journal of Structural Mechanics，1996，29(3/4):103 －114.

［11］ASCE.Manuals and reports on engineering practice No.78:structural fire protection［R］.American Society of Civil Engineers.New York:［s.n.］，1992.

［12］European Code 3.Design of steel structures part 1－2:general rules－structural fire design［S］.Brussels:CEN，2005.