一种高效的外辐射源雷达高径向速度目标实时检测方法

关 欣 胡东辉 仲利华④ 丁赤飚

①(中国科学院电子学研究所 北京 100190)

②(中国科学院空间信息处理与应用系统技术重点实验室 北京 100190)

③(微波成像技术国家重点实验室 北京 100190)

④(中国科学院研究生院 北京 100190)

1 引言

外辐射源雷达是本身不发射电磁波，利用广播、电视等信号作为辐射源的被动雷达系统，具有反隐身、抗低空突防及生存能力强等优点，是当前国内外研究热点[1]。目前，国外多家机构已开展了相应技术的研究，针对系统性能、被动相干技术、杂波抑制、目标定位及跟踪、波形特点等开展了研究工作[2-5]。而国内多家单位也开展了相关技术研究及实验[6-8]。但外辐射源雷达信号处理领域仍存在一些亟待解决的问题。

外辐射源雷达研究的核心问题是在强干扰中检测弱目标。通常雷达接收到的直达波、杂波信号远强于目标回波，在对直达波、杂波抑制后，仍需计算时延-多普勒 2维相关(模糊函数)以获取积累增益。然而，传统的FFT法实现模糊函数计算量大，难以达到实时。目前存在的模糊函数快速实现方法[9,10]：如预加权分级抽取FFT法、多级滤波的预加权ZFFT法等，降低了计算量，但实现过程仍较复杂，其中预加权会存在较大存储量的问题。为达到实时处理，本文采用基于分时处理的2维相干积累快速方法[11]，即通过信号分段，段内匹配滤波，段间FFT获取目标多普勒信息，来实现实时相干积累。

此外，在相干积累过程中，高径向速度目标会产生距离徙动，导致能量扩散，信噪比降低，而降低了目标检测能力。关于徙动校正已存在一些研究工作，如包络插值法[12]，对1维信号插值以补偿包络变化，但依赖于目标速度的先验知识，不适于实际应用；修正模糊函数方法[13]，加入速度、加速度影响因子，也需要一定先验知识。其他方法也多基于模糊函数计算进行徙动校正[14]，实现较为复杂，且实时性较差。此外，还存在基于速度标定及非相干积累的校正方法[15]：将数据分段，各段分别相干积累后，进行速度标定，再非相干积累，会引起增益损失，且不适于存在多普勒徙动的情况。

基于上述情况，本文介绍了基于分时处理的实时相干积累方法，并给出了一种适于实际应用的改进分时方案。文中将基于分时的相干积累及keystone变换校正距离徙动相结合，提出了一种高效的外辐射源雷达高径向速度目标实时检测方法，由于基于分时处理的相干积累方法与徙动校正可非常有效地结合，无需额外处理、易于实现。本文所提出的算法特点在于可以实现积累及徙动校正的实时处理，同时保证较高的校正效率。仿真及实测数据处理表明算法具有很高的实时性，能同时处理多目标场景，无需先验知识。对高径向速度目标，徙动校正后积累增益有很大提高，增强了系统的微弱目标检测能力。

2 外辐射源雷达回波信号模型

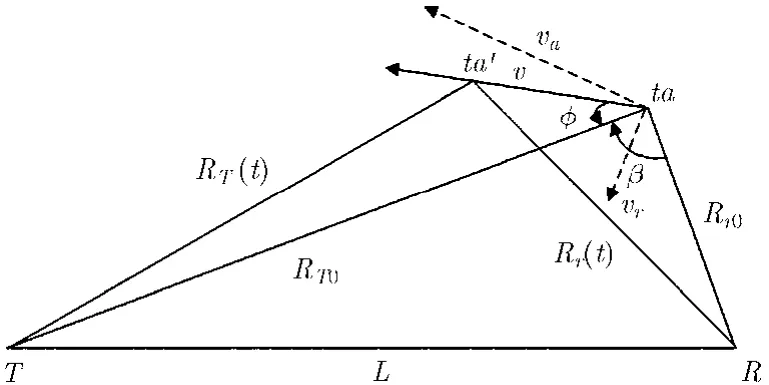
图1 外辐射源双站结构示意图

外辐射源雷达为双基地结构，其示意图如图 1所示。T为发射源，R为接收站，L为基线距离。假设目标初始位置为ta，距发射源初始距离为RT0，距接收站初始距离为Rr0，目标做匀速直线运动，速度为v,t时刻运动至ta'。β为双基地角，φ表示目标运动方向。若发射源基带信号为s(t)，任意时刻t目标回波信号延时为τ=R(t)/c，其中

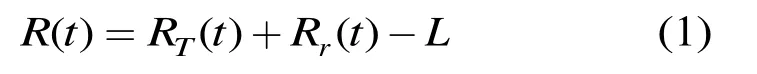
c为光速。此时回波信号模型为

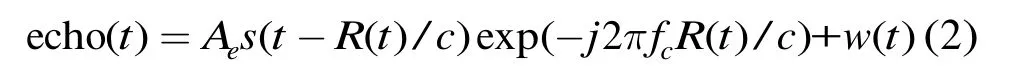
式(2)中，echo(t)为回波信号，fc为载波频率，A为回波信号幅度，w(t)为噪声。

由图1几何关系可得

所以

将式(5)在t=0处进行Taylor展开，则有

其中rT(t),rr(t),r(t)为高次项。vr=vcos(φ+β/2)为目标径向速度。由式(2)和式(6)，忽略高次项，可得

其中τ0=(RT0+Rr0-L)/c为初始延时，τ(t)=2vrcos(β/2)t/c为延时随时间变化项，目标多普勒频移fd=2vrcos(β/2)/λ。对回波信号采样，采样间隔为Δ，则有

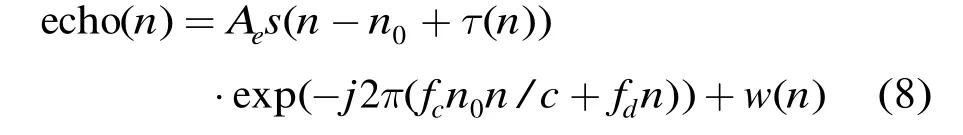
其中n0=τ0/Δ,τ(n)=2vrcos(β/2)t/Δ/c。

此外，雷达接收机参考天线接收直达波作为参考信号，表示为

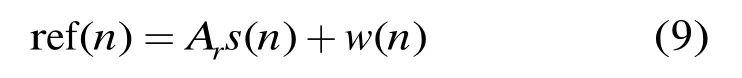
由式(8)可以看出，由于存在随时间变化项τ(t)，使得回波信号包络随时间发生变化，产生距离徙动，相干积累后会产生增益损失。采用相干积累检测时，高径向速度目标在积累时间内会跨越多个单元，导致信号能量在距离方向发生扩散，造成主瓣展宽及信噪比降低，随积累时间增加，信噪比逐渐恶化，因而降低了对目标的检测能力。现有方法实时处理较难，因此本文提出一种基于分时处理的相干积累及 keystone变换校正距离徙动的实时相干积累算法，实现高速目标的高效、实时检测。

本文信号模型基于匀速运动目标进行分析，对于高速运动目标，可能会存在目标非匀速运动产生高阶项，影响积累及校正结果，可采用的校正高次项方法包括基于分数阶傅里叶变化的二次项补偿方法[12]，RFT(Radon Fourier Transform)[16]等，通过搜索方法可对含高次项的目标进行校正。

3 基于2维分时滤波的实时相干积累方法

外辐射源雷达中通过相干积累获取一定积累增益，传统相干积累方法常用模糊函数实现，公式如式(10)：

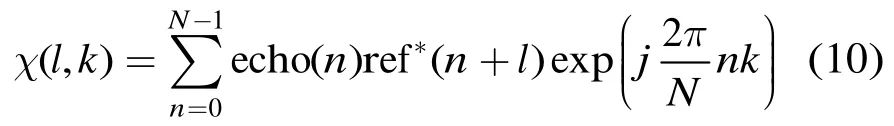
其中echo(n)为回波信号，ref(n)为参考信号，l为延时，N为数据长度，“*”表示共轭。一种常用的模糊函数计算方法采用FFT实现。若计算L个延时的模糊函数，则计算量为L(N+N/2log2N)。对于1 s积累时间，9 MHz采样率数据，计算量为 1315 GFlops，难以实时实现。

本文采用另一种实现相干积累的原理，采用 2维分时处理方式[11]，使用类似于调频连续波雷达中的积累方法，与SAR成像的原理一致，将1维信号做分时处理，划分为快时间和慢时间，利用运动目标多普勒信息进行相干积累检测，并实现实时处理。本文采用这种快速的相干积累方法，并给出一种适于应用的重叠不等长分段方法，对算法实时处理能力进行了验证，具体步骤为：

步骤 1 分时处理，将 1维的回波信号与参考信号分段，各段可等效为一个脉冲，构成2维矩阵，等效脉冲内为快时间，各脉冲间为慢时间。基本分时处理方法如图 2(a)所示。本文结合实际需要，给出一种适于实际应用的分段方法如下：

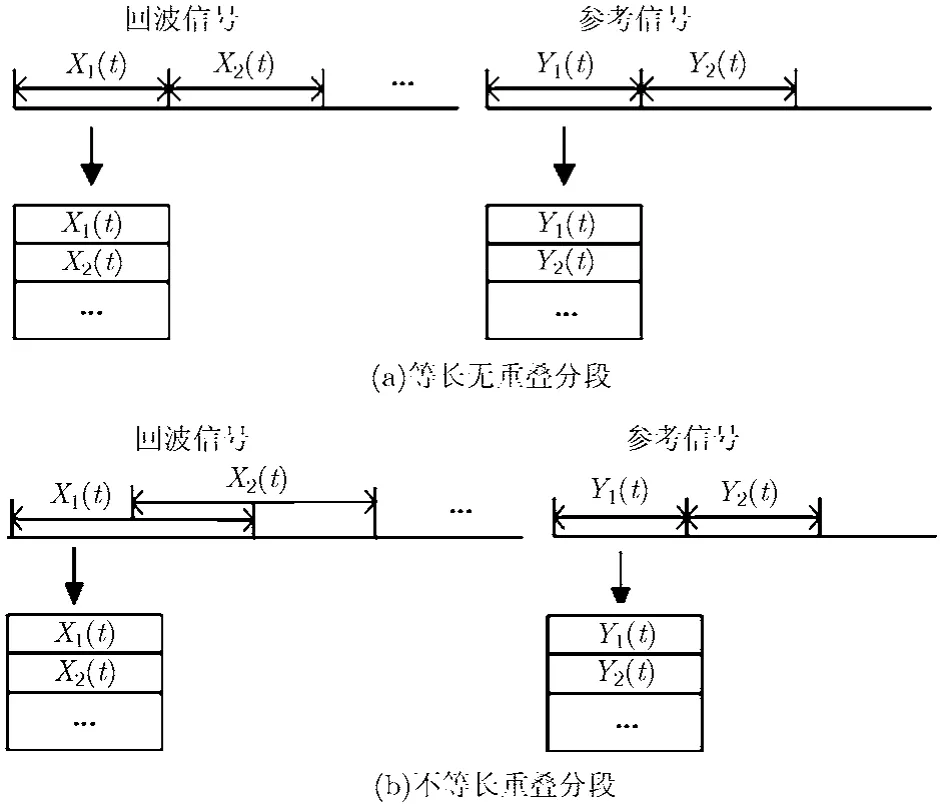
图2 分段方法示意图

首先，根据系统所需探测目标最大速度确定等效脉冲重复频率(PRF)，得到分段数N=4vmaxT/λ,vmax为所需最大不模糊速度，T为积累时间，λ为波长。按分段数目对参考信号分段，每段的有效长度为Lr=L/N,L为总数据长度。

对回波信号分段时采用重叠分段方法，以保证探测距离，同时若回波与参考信号采用相同的等效脉冲长度，由于较远距离门处目标的积累增益较低，会造成近距的直达波杂波增益大于远距离目标增益的问题。若所需最大探测距离为Rmax，由回波信号与参考信号每段长度之差决定最大检测距离，可保证在检测范围内具有相同增益，则回波信号长度Le=Lr+2fsRmax/c,fs为采样率，c为光速，为保证分段数目，采取重叠分段方式，如图2(b)所示。

最后，对参考信号补零，保证每段长度与回波信号长度等长。

在上述分段方法中，等效PRF及等效脉冲长度不存在相互制约关系，可根据实际需要分别选取，实际使用是可尽量保证目标不存在速度模糊、盲速、距离模糊。当已经存在PRF设计较小情况，会出现盲速及速度模糊现象。对于盲速，可采用变PRF方法，同时计算不同等效PRF情况下的两组(或多组)结果，经数据融合处理，即可去除盲速现象。针对速度模糊下徙动校正，可对校正结果按不同模糊数进行相位补偿及数据融合[17]，可采用并行处理，以满足实时要求。通常情况下通过设计PRF即可避免上述现象。分段方法适于发射连续波的外辐射源，本文以DTTB数字电视信号为例，针对通常预警雷达所需探测目标速度，以两倍音速的观测需要为例，分段数约为6000段，各段长度在15000以上，可满足常规应用需求。

步骤 2 回波信号与参考信号，各对应等效脉冲间通过匹配滤波(FFT频域实现)实现距离向脉冲压缩。以第nm个等效脉冲为例：

nf,nm分别为快时间、慢时间。

步骤 3 各段间通过 FFT获取目标多普勒信息。

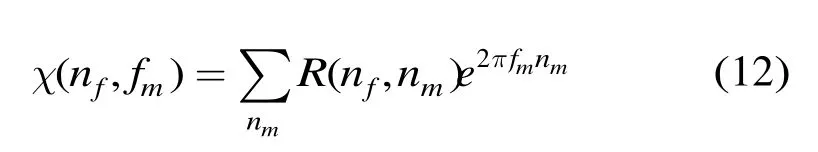
χ(nf,nm)即为2维相干积累结果。

由于分时处理后各等效脉冲长度降低，若等效PRF(脉冲重复频率)为M，则等效脉冲长度降低了M倍，极大地降低了相干积累的运算量。此时，每个等效脉冲需要计算N/M次复乘，以及 3次长度为N/M的FFT运算，共M(N/M+3N/2M* log2N/M)，沿慢时间多普勒滤波：L次长度为M的FFT，共L(M* log2M)。总计算量为M(N/M+3N/2M·log2(N/M))+L(M·lo g2M)。由于N的数目很大，通过分段降低了每次计算FFT的长度，可急剧缩减计算量，且实现方法简单，适用性强。

对比传统模糊函数(CAF)方法(采用 FFT快速实现)计算量，总结如表1所示。加速比可达 103～104数量级。采用上述方法，可保证实时处理能力。由于通过分时进行相干积累，可在频域进行匹配滤波，在滤波处理过程中，可以很方便地在距离频域-慢时间域校正距离徙动，较传统模糊函数而言，特别适合采用keystone变换，无需额外的处理。同时较强的实时性更适于实际应用的需求。

表1 模糊函数实现相干积累与2维分时组合滤波法实现相干积累运算量对比

4 基于2维分时滤波的相干积累及keystone变换的距离徙动校正算法

本节基于前文所述相干积累方s法，加入适于实时处理的距离徙动校正，实现高径向速度目标的高效、实时检测。具体实现方法如下：

步骤 1 针对前文所述信号模型，进行分时处理，设各段内时间为快时间tf，段间为慢时间tm，假设目标在等效脉冲内无距离徙动，则距离随慢时间变化，由于信号与噪声不相关，省略噪声项则重构后信号矩阵为

根据式(6)可得回波信号表达式为

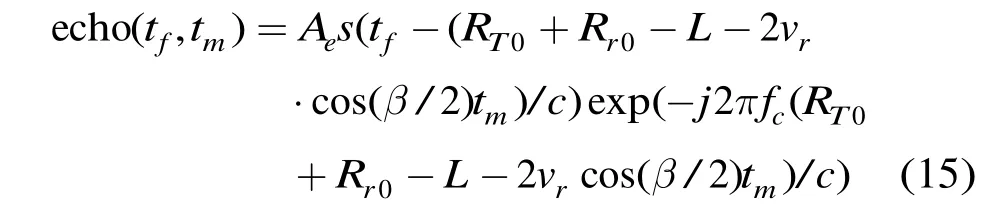
步骤 2 沿快时间匹配滤波(FFT频域实现)。式(14)和式(15)变换至快时间频域-慢时间域可表示为

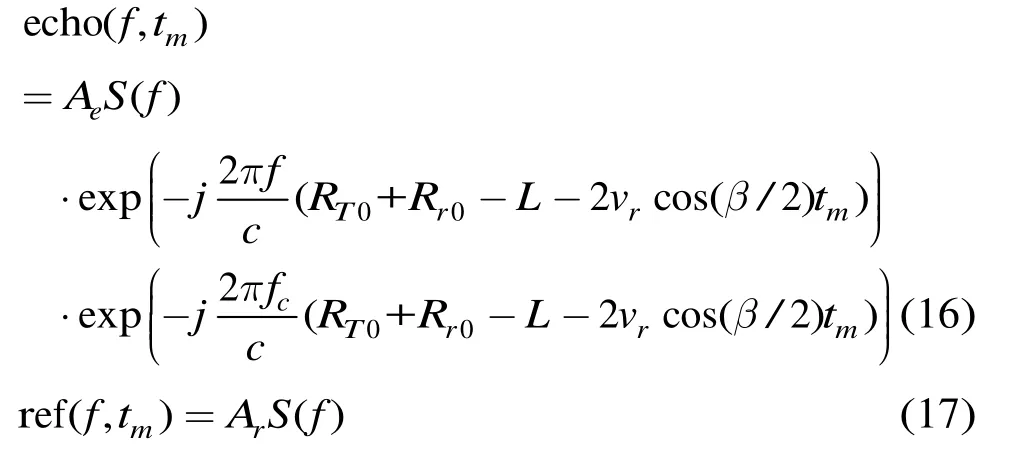
根据式(16)和式(17)，各段匹配滤波后为

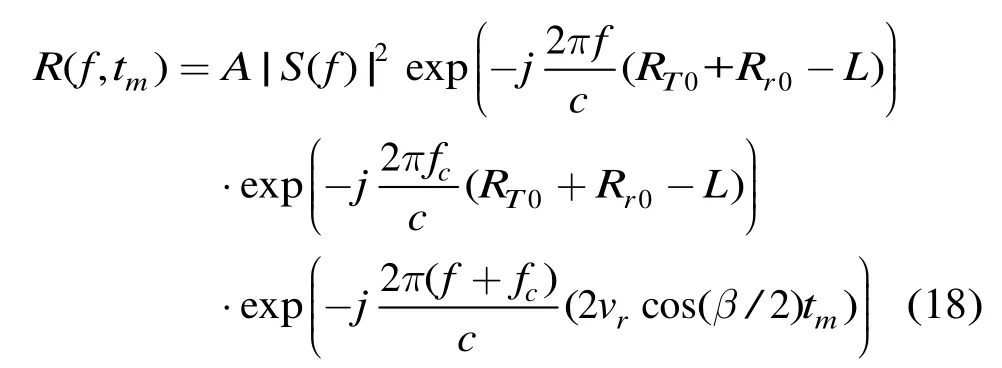
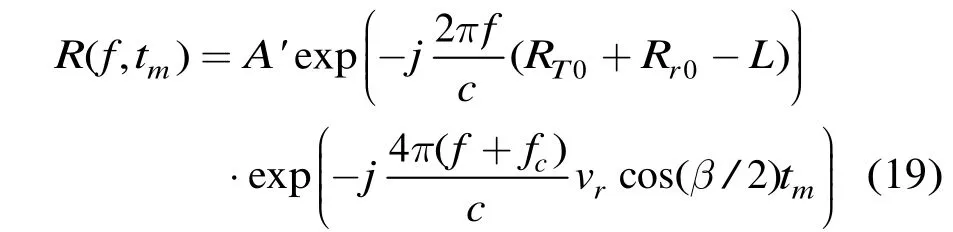
此时若不进行徙动校正，设s'(t)=IFFT(|S(f)|2)，匹配滤波后时域表示为

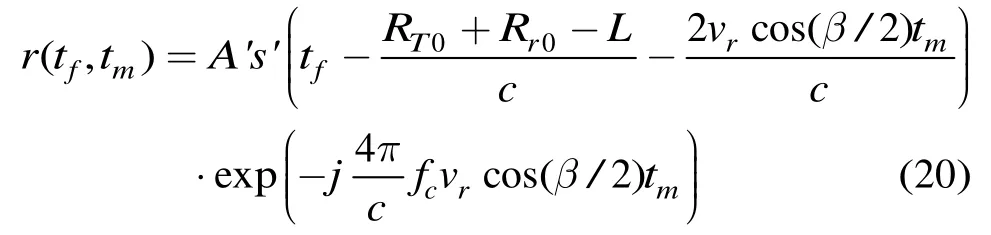
式(19)和式(20)表明，由于多普勒频率fd=2(f+fc)vrcos(β/2)/c随f变化，造成压缩后信号包络存在变化。当完成匹配滤波后，目标出现位置(延时单元)在各段间会产生变化，形成迁移曲线，匹配滤波后，产生能量分散，能量会沿距离方向扩散，表现为积累后峰值幅度的减低。对于不同径向速度目标，在1 s积累时间内，随目标速度增高，信噪比严重衰减，仿真验证可知当目标径向速度约为200 m/s时，信噪比损失近15 dB。而外辐射源雷达在实际应用中，目标速度可能达到2倍音速，甚至更高，此时信噪比恶化现象非常严重，会严重影响系统的检测能力。

步骤3 为校正多普勒频移随频率f的变化，可通过对慢时间进行尺度变换，应用keystone变换来校正包络。令tn为虚拟慢时间。

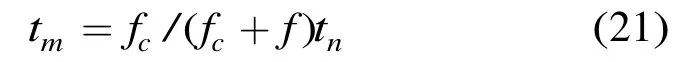
对式(18)进行keystone变换：

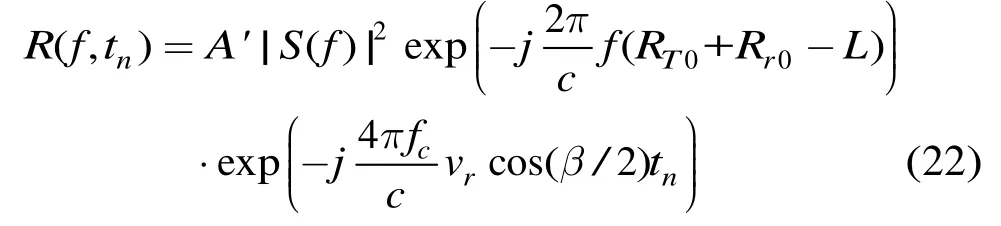
对采样后的离散信号进行keystone变换，可用插值法、Chirp-z变换等方法实现[18]，徙动校正过程与目标运动速度、位置无关，可同时对多目标同时实现徙动校正，且无需先验知识，易于实现及实时处理。

步骤4 上一步结果变换至距离-慢时间域则为

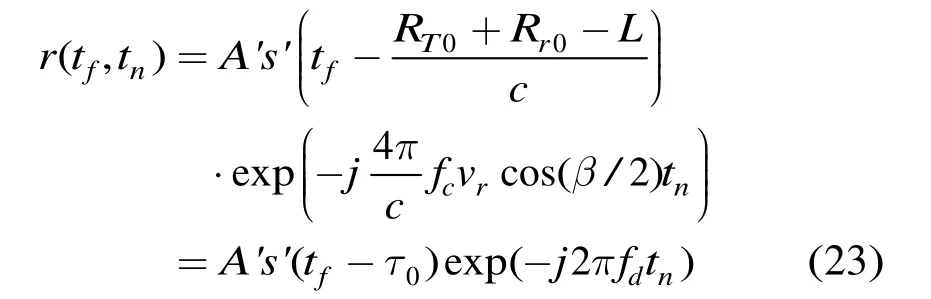
其中fd=2vrcos(β/2)/λ。此时不存在包络随时间的变化，则距离徙动得到了校正。

步骤5 沿时间FFT获取多普勒信息，得到相干积累结果χ(tf,fm)。

对相干积累获得的|χ(tf,fm)|采用恒虚警检测，在满足一定信噪比情况下，可检测出目标，同时获得目标延时、多普勒信息。对于高径向速度目标，经过徙动校正后，积累增益得到很大提高。算法提高了目标检测能力，是一种高效的高径向速度目标检测方法。处理算法流程如图3所示。

由于在相干积累过程中插入 keystone变换过程，不引人额外的运算，且keystone可用于多目标场景，易于实现，易于并行计算，具有较少的运算量，适于实时处理的需求。实测数据处理实时性分析如表2所示。

表2 相干积累与徙动校正运算速度

5 仿真分析及实际数据验证

上述内容中已对算法的实时性进行了分析及验证，本节重点分析徙动校正后算法的相干积累处理增益。

5.1 仿真数据分析

本节采用仿真数据分析本文所提方法的效果。根据GB20600-2006[19]规定，仿真DTTB数字电视信号，表3为系统仿真参数，表4为点目标仿真参数。

表3 仿真采用系统参数

表4 仿真目标参数及校正结果

不进行徙动校正及采用本文方法校正距离徙动后的结果局部图，如图4(a)、图4(b)所示，对比校正前后峰值幅度可知，采用本文方法后，徙动现象得到了很好的校正，信号能量更为集中，信噪比得到提高。

图3 算法处理流程图

图4 仿真数据处理结果

图4(c)、图4(d)分别表示快时间-慢时间域中沿快时间匹配滤波结果，可以看出校正前目标存在明显的迁移曲线，按本文所述方法采用keystone变换校正后，曲线得到了很好的修正，解决了因目标高速运动而引起的徙动问题。

此外，通过仿真验证了算法可应用于多目标场景，由于增加了信噪比，因而提高了对微弱信号的检测能力，对于部分低于检测门限的目标，经校正后检测能力可得到很大提高，增强了微弱目标的检测能力。由此可增加外辐射源雷达系统的作用距离。

为进一步分析算法应用于处于检测门限以下的微弱目标的检测效果，仿真径向速度0到190 m/s的目标，加入直达波、杂波及接收机噪声，分别采用本文方法进行处理，以分析不同速度目标校正后检测能力变化。

图5表示校正前后信噪比曲线，在徙动校正前，信噪比随目标径向速度增加而迅速衰减，采用本文方法，由速度引起的信噪比损失得到了很好的补偿，信噪比不再受到目标速度影响。对于高径向速度目标，经校正后，信噪比得到很大提升。由于直达波、杂波旁瓣及噪声的影响，图5中曲线在理论积累增益附近波动。

对仅存在目标的情况仿真分析，徙动校正能力如表5所示，算法具有较少的增益损失，此时损失包括分数阶采样造成的旁瓣效应等影响。此外采用插值实现徙动校正时，校正精度会受到插值精度影响。

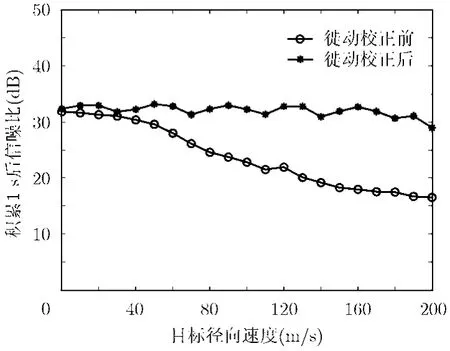
图5 徙动校正前后信噪比随速度变化曲线对比

表5 校正精度分析

5.2 实测数据分析

本节采用基于DTTB数字电视信号一组实测数据进行实验分析。实测数据的主要相关参数如表 6所示。

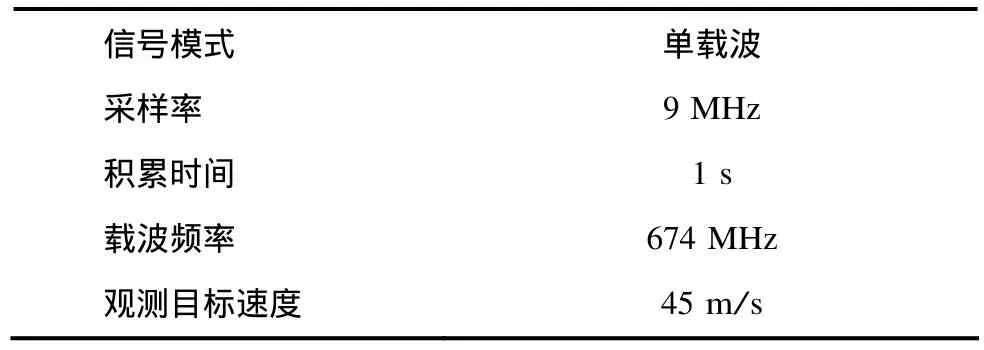
表6 实测数据相关参数

首先，采用变步长NLMS方法抑制直达波、杂波。之后，应用本文所述方法进行相干积累，以检测目标。图6(a)与图6(c)为未经距离徙动校正时相干积累检测，图6(b)，图6(d)为经keystone校正后的积累结果，均采用本文所述的实时2维相干积累方法。校正后徙动现象消失，信噪比提高了约 5.5 dB。信号的检测能力得到了明显提高。

6 结论

本文所述检测方法在基于分时处理的快速相干积累方法中，采用keystone变换校正高径向速度目标的距离徙动，能够在保证高径向速度目标积累增益的情况下，实现实时处理。文中采用一种适于实际应用的分段方法实现相干积累，并简要讨论可能存在的问题及解决方案。采用keystone变换可很好地补偿因目标运动造成的信噪比损失，因而可提高微弱目标的检测能力，并适于实时处理。通过仿真分析及实际数据验证，说明本文提出方法能够较大程度地提高信噪比，增加了外辐射源雷达系统的探测距离。算法无需依赖目标的先验信息，适用于多目标场景，增益损失小，且适于实时处理，是一种实时高效的高径向速度目标检测方法。

图6 实测数据处理结果

[1]Howland P. Passive radar systems[J].IEE Processings-Radar,Sonar and Navigation, 2005, 152(3): 105-106.

[2]Griffiths H D and Baker C J. Passive coherent location radar systems. Part 1: performance prediction[J].IEE Processings-Radar,Sonar and Navigation, 2005, 152(3): 153-159.

[3]Griffiths H D and Baker C J. Passive coherent location radar systems. Part 2: waveform properties[J].IEE Processings-Radar,Sonar and Navigation, 2005, 152(3): 160-168.

[4]Howland P E, Maksimiuk D, and Reitsma G. FM radio based bistatic radar[J].IEE Processings-Radar,Sonar and Navigation, 2005, 152(3): 107-115.

[5]Palmer J, Palumbo S, and Summers A. An overview of an illuminator of opportunity passive radar research project and its signal processing research directions[J].Digital Signal Processing, 2011, 21(5): 593-599.

[6]王俊, 水鹏朗, 保铮. 基于分数迟延估计的外辐射源雷达杂波相消算法[J]. 西安电子科技大学学报(自然科学版), 2005,32(3): 378-382.

Wang Jun, Shui Peng-lang, and Bao Zheng. External illuminator based continuous wave radar clutter canceling algorithm using arrival time estimation by fractional interpolation[J].Journal of Xidian University, 2005, 32(3):378-382.

[7]高志文, 陶然, 单涛. DVB-T辐射源雷达信号模糊函数的副峰分析与抑制[J]. 电子学报, 2008, 36(3): 505-509.

Gao Zhi-wen, Tao Ran, and Shan Tao. Side peaks analysis and suppression of DVB-T signal ambiguity function for passive radar[J].Acta Electronic Sinica, 2008, 36(3): 505-509.

[8]Gao Zhi-wen, Tao Ran, and Wang Yue. Analysis and side peaks identification of Chinese DTTB signal ambiguity functions for passive radar[J].China Science in China Series F:Information Sciences, 2009, 52(8): 1409-1417.

[9]高志文, 陶然, 单涛. 外辐射源雷达互模糊函数的两种快速算法[J]. 电子学报, 2009, 37(3): 669-672.

Gao Zhi-wen, Tao Ran, and Shan Tao. Two fast algorithms of cross-ambiguity function for passive radar[J].Acta Electronic Sinica, 2009, 37(3): 669-672.

[10]Zhuo Zhi-hai, Shan Tao, and Tao Ran. Fast computation of cross-ambiguity function[J].Journal of Beijing Institute of Technology, 2008, 17(4): 466-471.

[11]Berge C R, Demissie B, and Heckenbach J. Signal processing for passive radar using OFDM waveforms[J].IEEE Journal of Selected Ttopics in Signal Processing, 2010, 4(1): 226-238.

[12]杨金禄, 单涛, 陶然. 数字电视辐射源雷达的相参积累徙动补偿方法[J]. 电子与信息学报, 2011, 33(2): 401-411.

Yang Jin-lu, Shan Tao, and Tao Ran. Method of migration compensation in coherent integration for digital TV based passive radar[J].Journal of Electronics&Information Technology, 2011, 33(2): 401-411.

[13]Malanowski M, Kulpa K, and Olsen K E. Extending the integration time in DVB-T based passive radar[C].Proceedings of the 8th European Radar Conference,Manchester UK, 2011: 190-193.

[14]Liu Lei, Tao Ran, and Zhang Nan. The CAF-DFRFT-KT algorithm for high-speed target detection in passive radar[C].2011 International Conference on Instrumentation,Measurement, Computer, Communication and Control,Beijing, 2011: 748-751.

[15]杨金禄, 单涛, 陶然. 外辐射源雷达高速加速微弱目标检测研究[J]. 现代雷达, 2011, 33(5): 30-35.

Yang Jin-lu, Tao Ran, and Shan Tao. A study on external illuminating radar detection of weak targets with a high speed and acceleration[J].Modern Radar, 2011, 33(5): 30-35.

[16]Jia Xu, Ji Yu, Peng Ying-ning,et al.. Radon-Fourier transform(RFT)for radar target detection(I): generalized Doppler filter bank[J].IEEE Transactions on Aerospace and Electronic System, 2011, 47(2): 1186-1202.

[17]余吉, 许稼, 汤俊, 等. 基于Keystone变换的改进雷达目标长时间积累[J]. 雷达科学与技术, 2008, 6(6): 454-458.

Yu Ji, Xu Jia, Tang Jun,et al.. An improved keystonetransform based method for long-time coherent integration of radar target[J].Radar Science and Technology, 2008, 6(6):454-458.

[18]徐冠杰. 雷达信号长时间积累对微弱目标检测的研究[D]. [硕士论文], 西安电子科技大学, 2011.

Xu Guan-jie. Study o long-term integration method for detection of weak target[D]. [Master dissertation], Xidian University, 2011.

[19]中国国家标准化管理委员会. 国标: 20600-2006. 数字电视地面广播传输系统帧结构、信道编码和调制[S]. 2006.

SAC(Standardization Administration of the People’s Republic of China). GB: 20600-2006. Framing Structure,Channel Coding and Modulation for Digital Television Terrestrial Broadcasting System[S]. 2006.