高速移动无线图像传输链路误差分析
孙士洁,赵怀慈,郝明国
(1.中国科学院 沈阳自动化研究所,辽宁 沈阳 110016;2.中国科学院大学,北京 100039;3.中国科学院 光电信息处理重点实验室,辽宁 沈阳 110016;4.辽宁省图像理解与视觉计算重点实验室,辽宁 沈阳 110016)
目前,无线图像传输技术在军事和民用诸多领域均已得到广泛应用,但在带宽、能量等资源受限条件下,实现“高速运动中”无线图像高质量、高速率、高可靠的实时传输仍然是一个非常有挑战性的问题:1)压缩图像数据敏感。高效压缩编码使图像数据码流对信道传输差错愈加敏感,通过信道后产生的错误无法定位,且可能在时间和空间上扩展。2)无线传输信道复杂。无线传输信道受周围环境物理属性影响,阴影衰落、多径干扰等条件很难遍历,各种突发干扰也无法准确预知。3)误差特性描述困难。无线传输过程中,图像数据发生错误往往具有相关性,错误比特长度、发生频率及位置等特征难以用精确的数学语言进行描述。因此,进行无线图像传输系统方案设计、论证,减小硬件系统开发风险和成本,确保所设计系统在高速移动条件下保持鲁棒性,准确理解整个无线图像传输链路的错误属性与传递规律至为关键。
对于通信链路误差建模,现有方法主要是根据误差描述的精细程度选取转移状态数量,构建有限或无限状态马尔科夫链和隐性马尔科夫链误差模型[1-3]。这些模型要准确描述链路误差特征,需要确定的参数较多,算法也十分复杂。为此,本文在分析无线图像传输系统链路误差转换过程基础上,借鉴“瑞士奶酪模型”思想,提出了高速移动无线图像传输误差链概念模型,以帧差错间隔、帧内误比特数和错误位置为随机变量,采用具有两个参数的Weibull分布近似帧差错间隔与帧内误比特数样本统计分布,并假定错误位置样本分布服从均匀分布,建立了一种简单而灵活的高速移动无线图像传输链路误差模型,并对所提出的误差模型性能进行了仿真和验证。仿真结果表明,所提出的误差模型比较准确地反映了真实高速移动无线图像传输系统的链路误差特性,进而验证了误差模型的正确性与有效性。
1 无线图像传输系统误差链概念模型
无线图像传输过程是为实现特定应用目的而对图像信息进行一系列转换或变换的活动。这些信息转化活动都不可避免地会造成原始图像信息的丢失并引入一定量误差,同时,各种误差在信息传递与转换过程中也会发生抵消、扩大或累积等现象,构成一种链式关系,所有的链式关系共同组成了误差信息传输链,即误差链。如图1所示,按照典型数字通信系统构成[4],无线图像传输误差链可由图像获取环节、图像预处理环节、图像发送环节、信道传输环节、图像接收环节和图像重构环节所组成。
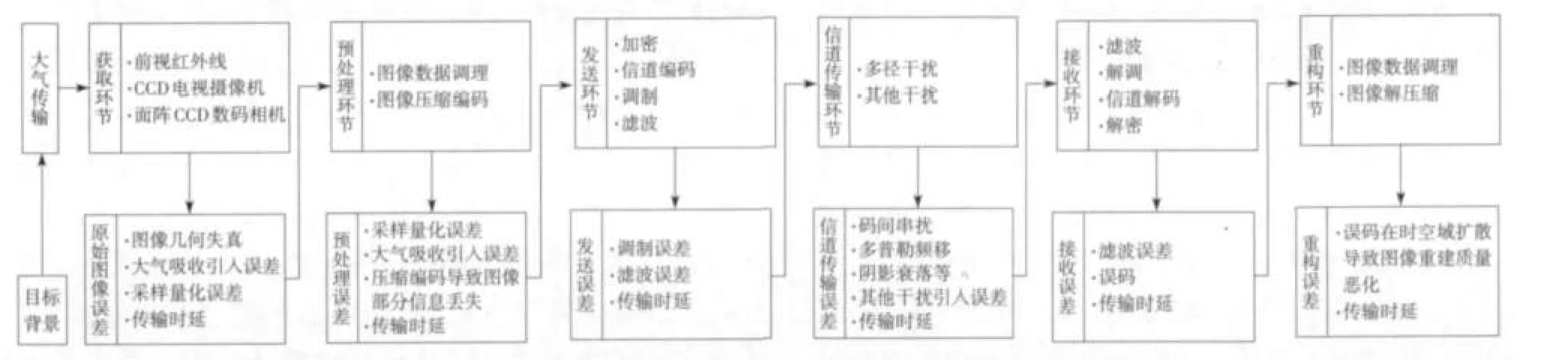
图1 高速移动无线图像传输误差链
图1中6个环节误差转换关系简要描述如下:1)在图像获取环节,目标背景反射或辐射能量经大气衰减、吸收后被传感器感受,并通过采样、量化完成原始图像数字化处理。在此过程中,误差来源主要是大气传输引入的目标背景发射与辐射能量损失、传感器和光学系统引发的图像几何失真和图像数字化处理过程采样量化误差,以及信息传输时延。2)预处理环节重点完成原始数字图像的压缩编码,误差主要包括前一环节中采样量化与大气吸收引入误差、压缩编码导致图像部分信息丢失以及信息传输时延。3)发送环节包含从加密、信道编码、调制到滤波、射频的全部信号处理过程,误差主要由对预处理环节数字图像信号的调制误差、滤波误差和传输时延组成。4)信道传输过程中,多径干扰和其他电磁干扰主要导致数字图像传输信号的码间串扰、阴影衰落等,以及图像传输系统收发终端相对运动引起的非常大的多普勒频移。5)接收环节组成与发送环节相反,包括射频、滤波、解调、信道解码和解密等信息处理单元,误差组成主要表现为误码和传输时延。6)重构环节主要完成图像重构,前述各环节误差在这个环节表现为误码在时空域扩散引起的图像分组数据包丢包、包错误以及传输时延,最终导致重构图像质量严重恶化。
基于上面分析,借鉴安全科学领域“瑞士奶酪模型”[5]的思想(即所有系统都是由若干基本要素构成,每个基本要素中存在的漏洞或缺陷形如每片奶酪上的孔洞,且孔洞的位置和大小不断变化,当所有奶酪上的孔在瞬间排列在一条直线上时,形成“事故机会弹道”,危险就会穿过所有基本要素导致事故发生),以误差链中各环节为基本要素,以各环节中存在误差为漏洞或缺陷,形成高速移动无线图像传输误差链概念模型,如图2所示。
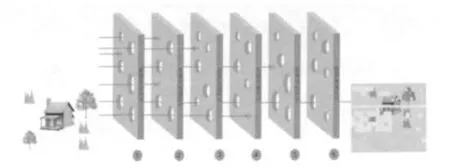
图2 高速移动无线图像传输误差链概念模型
2 高速移动无线图像传输系统误差链分析与建模
2.1 统计参数选取
高速移动无线图像传输时,各种链路误差因其属性不同对图像重建质量的影响比重差异很大。如图像获取环节形成待传输的原始图像信息,经无线传输后要求重建图像可以最大限度地准确再现这些原始图像信息,而大气环境、采样量化等引入的误差造成原始图像信息与真实目标背景间的差异,与图像重建质量无因果关系;相反,信道传输环节中,多径干扰、阴影效应和多普勒频移等引入的误差,直接导致图像数据解码的误码,成为引发图像重建质量恶化的关键因素。加之各种链路误差在传递过程中,其属性和形式也发生变化且转换复杂,很难用数学形式确切描述。因此,高速移动无线图像传输系统误差链,需要根据应用需求,选取适当的统计参量进行分析。
考虑实际无线图像传输系统中,图像数据是根据所采用数据链路层协议封装成帧,以“帧数据”形式进行传输;而每帧数据中错误发生是随机的,且错误比特因发生位置不同导致其在数据帧内或相关数据帧之间扩展,直接造成端到端无线图像传输质量恶化。因而,建立无线图像传输系统链路误差模型,主要考虑引入以下统计参量[6-7]:
1)帧差错间隔(Frame Error Separation,FES),表示两个连续发生损坏的数据帧之间的间隔;
2)帧内误比特数(Number of Error per Corrupted Frame,NECF),表示每个损坏的数据帧中错误比特个数;
3)错误位置(Error Location,EL),表示每个损坏的数据帧中每个错误比特在该数据帧所处的位置。
基于上述3个统计参量,可以给出高速移动无线图像传输数据流的帧结构,如图3所示。帧差错间隔与帧内误比特数的分布规律,可以通过对大量实测数据的统计分析,并采用曲线拟合方法分别得到其概率密度函数。文献[7]中,以数字视频广播系统为例,将帧差错间隔、帧内误比特数和错误位置的统计特性分别用离散的指数分布、高斯分布与均匀分布近似描述,在此基础上,采用这3个随机变量建立了误差模型并验证其有效性。
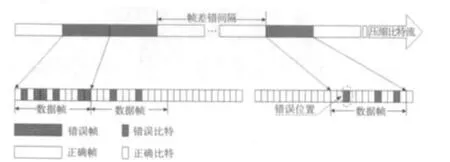
图3 无线图像传输数据流的帧结构
2.2 误差模型的建立
建立误差模型实质上就是选取反映误差特征的统计参量,并将其统计特性用经典的概率分布或随机过程近似描述的过程。遵循这一误差模型设计思想,本节在文献[7]的基础上,以帧差错间隔、帧内误比特数和错误位置为随机变量,提出以两个参数的Weibull分布分别替代离散的指数分布和高斯分布,对帧差错间隔与帧内误比特数的统计特性进行近似,以均匀分布近似错误位置样本统计特性,建立高速移动无线图像传输链路误差模型。
Weibull分布主要用于可靠性工程和失效分析领域,因它具有多功能性,可通过参数调整获得近似指数分布、正态分布等分布形式,因而在天气预报、生存分析以及通信系统工程等诸多领域都有广泛的应用。具有两个参数的Weibull分布概率密度函数定义为[8]式中:a和b分别为尺度参数和形状参数。确定这两个参数的具体步骤如下:
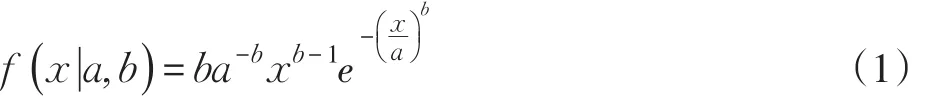
1)设定高速移动无线图像传输场景条件,进行图像传输试验并存储接收图像数据,形成分析图像传输链路误差统计特性的样本数据集;
2)分析样本数据集的帧差错间隔与帧内误比特数的统计特性,计算帧差错间隔、帧内误比特数的样本统计均值、方差及概率分布;
3)采用曲线拟合方法,以Weibull分布近似帧差错间隔与帧内误比特数的样本概率分布,进而确定a和b数值。
如图4所示,采用H.264+RS+OFDM方案的无线图像收发系统,在车载高速移动条件下实测无线图像传输试验的样本数据集,经统计分析形成的样本FES分布和NFES分布,并将两个样本分布与采用指数分布、高斯分布和具有两个参数的Weibull分布的近似描述进行了对比。从图4中可以看出,确定适当的尺度和形状参数,Weibull分布对样本FES分布和NFES分布的近似效果要好于指数分布和高斯分布。
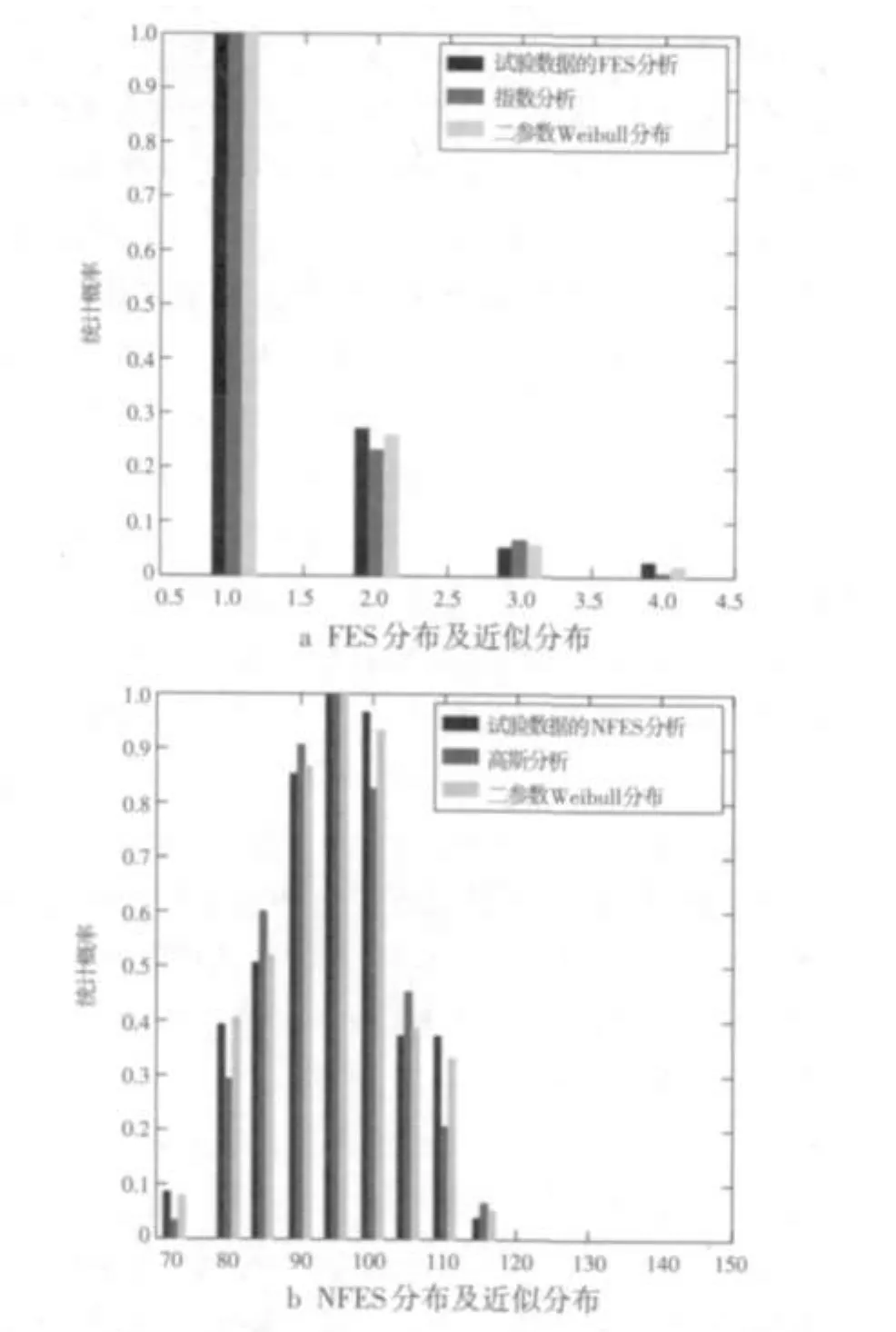
图4 信噪比为20 dB条件下高速移动无线图像传输样本FES分布和NFES分布及其近似分布
3 仿真实验及验证
3.1 仿真方案设计
为验证所提出误差模型的有效性,仿真实验设计方案如图5所示。该方案中,视频序列传输分两路处理:一路是原始视频序列经H.264编码器后,加入误差模型生成的错误序列,然后由H.264解码器完成解码,整个过程由软件仿真实现;另一路是在车载高速移动条件下,由采用H.264+RS+OFDM方案设计的无线图像收发硬件系统进行实测。最终,以重构视频序列的峰均值信噪比(PSNR)作为检验误差模型有效性的参考标准。
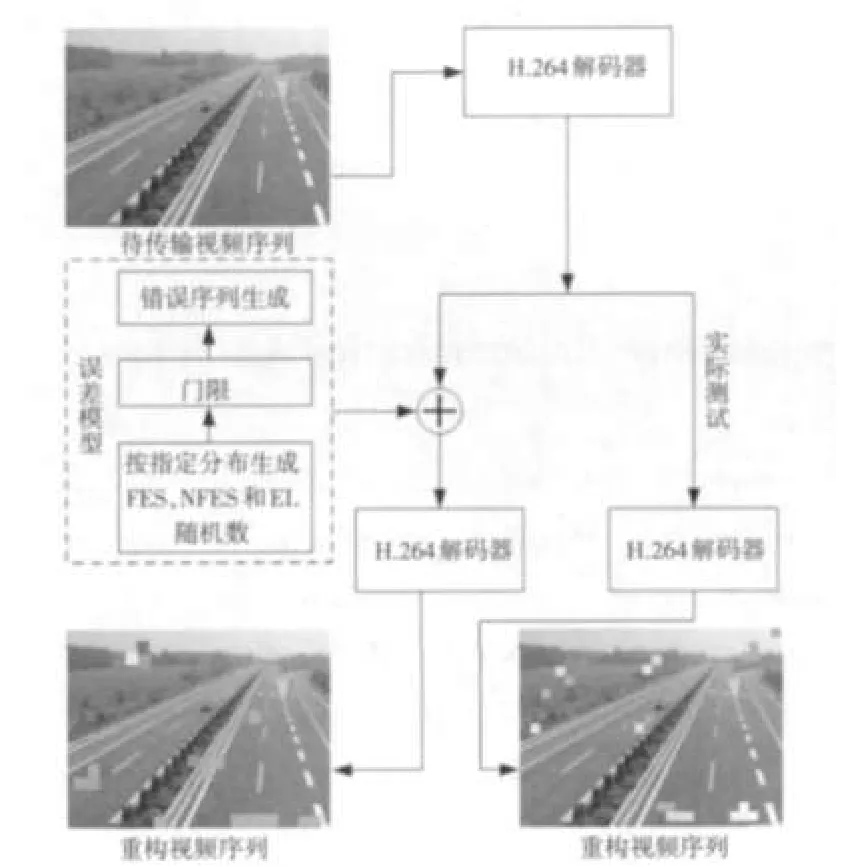
图5 仿真实验原理图
3.2 仿真实验
依据仿真方案,在不同信噪比(EbN0)条件下进行了误差模型的性能仿真,并将仿真结果与高速公路环境下的硬件系统实际测试结果进行了对比,如表1所示。比较表1中两组PSNR值,结果表明本文所提出的误差模型比较准确地反映真实高速移动无线图像传输系统的链路误差特性,进而验证了误差模型的正确性与有效性。
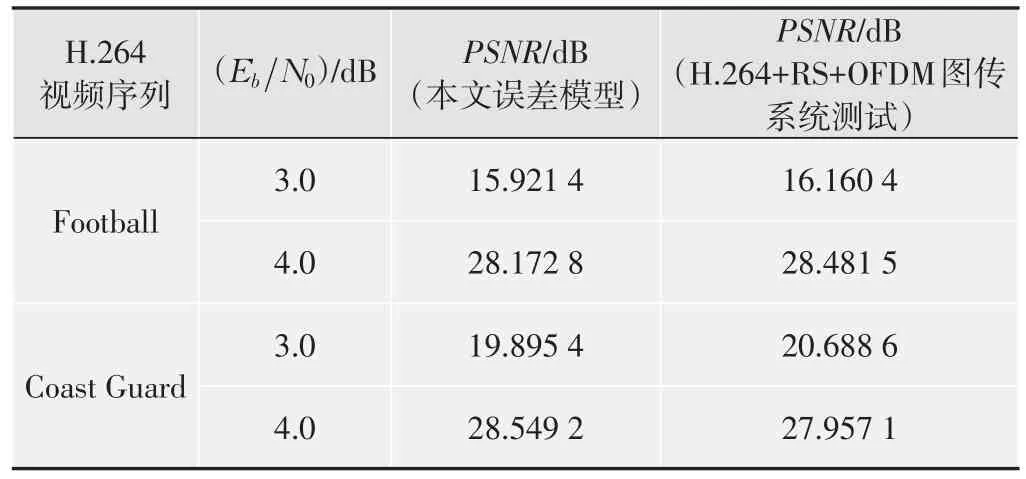
表1 H.264视频重建质量评估
4 小结
本文在分析无线图像传输系统链路误差转换过程基础上,借鉴“瑞士奶酪模型”思想,提出了高速移动无线图像传输误差链概念模型;以两个参数Weibull分布近似表示帧差错间隔和帧内误比特数样本统计特性、均匀分布近似表示错误位置样本统计特性,建立了具有3个随机变量的高速移动无线图像传输误差链模型,并以PSNR值为指标对所提出的误差链模型性能进行了仿真和验证。仿真结果表明,所提出的误差模型比较准确地反映了真实高速移动无线图像传输系统的链路误差特性,进而验证了误差模型的正确性与有效性。
[1] BAI Haowei.Error modeling schemes for fading channels in wireless communications:a aurvey[J].IEEE Communications Surveys&Tutorials,2003,5(2):2-9.
[2]SALIH O S,WANG C-X,LAURENSON D I.Three layered hidden markov models for binary digital wireless channels[C]//Proc.IEEE International Conference on Communicaitons.[S.l.]:IEEE Press,2009:1-5.
[3]ROBERT P N,DARWISH A M,REED J W.Fast bit error generation for simulation of MPEG-2 transmission in wireless systems[C]//Proc.IEEE Wireless Communications and Networking Conference.[S.l.]:IEEE Press,1999:324-328.
[4]SKLAR B.数字通信原理与应用[M].徐平平,宋铁成,叶芝慧,等,译.2版.北京:电子工业出版社,2002.
[5] REASON J.Human error[M].New York:Cambridge University Press,1990.
[6]FARRUGIA R A,DEBONO C J,MICALLEF P.Channel modeling and simulation of a Ka-band videoconferencing system[C]//Proc.IEEE Mediterranean Electrotechnical Conference.[S.l.]:IEEE Press,2006:613-616.
[7] FARRUGIA R A,DEBONO C J.A statistical bit error generator for emulation of complex forward error correction schemes[C]//Proc.IEEE International Conference on Communications.[S.l.]:IEEE Press,2007:177-182.
[8]MURTHY D N P,XIE M,JIANG R.Weibull models[M].[S.l.]:John Wiley & Sons,Ltd.,2004.

