拓广探究，凸显直角梯形“垂直”美

☉江西省大余中学 廖达凡 杨 红

《义务教育课程标准实验教科书》人教版数学八年级下册“19.3梯形”中讲授直角梯形时只给出定义：“有一个角是直角的梯形叫做直角梯形”.除此外，教材中并没有占用更多的笔墨去探讨直角梯形，但从定义中不难看出，“垂直”是直角梯形一个显著的特征.倘若拓广探究直角梯形上、下两底之和等于其中一腰时，笔者发现更能凸显直角梯形“垂直”美的个性.

一、探究“上、下两底之和等于斜腰”的直角梯形中的“垂直”美

探究1 如图1，直角梯形ABCD中，AD∥BC，∠ABC=90°，AD+BC=DC.

（1）在线段DC上是否存在一个点E，使得AE⊥BE？若存在，请找出并证明；若不存在，请说明理由.

（2）在线段AB上是否存在一个点M，使得DM⊥CM？若存在，请找出并证明；若不存在，请说明理由.

（3）若（1）（2）问中满足条件的点E、M存在，请进一步探究是否有ME⊥DC？请说明理由.

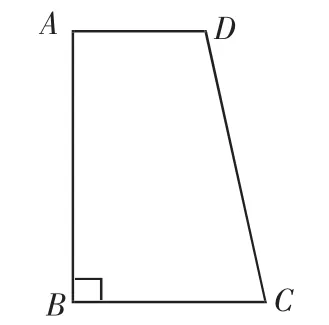
图1

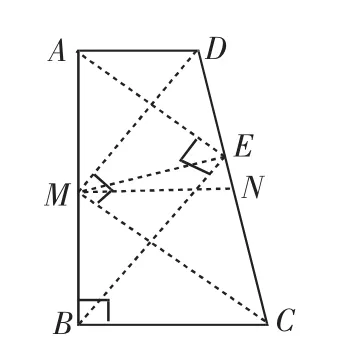
图2

解析：（1）存在.

如图2，在线段DC上截取DE=DA，则EC=BC，连接AE、BE，此时AE⊥BE.证明如下.

由DA=DE，EC=BC，得∠DAE=∠DEA，∠CEB=∠CBE，

则∠ADE=180°-2∠DEA，∠BCE=180°-2∠CEB.

由AD∥BC，得∠ADE+∠BCE=180°，

则180°-2∠DEA+180°-2∠CEB=180°.

即∠DEA+∠CEB=90°.

即∠AEB=90°.

即AE⊥BE.

（2）存在.

如图2，取线段AB的中点M，连接DM、CM，此时，DM⊥CM.证明如下.

取线段DC的中点N，连接MN，

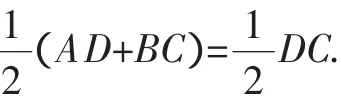
则DN=CN=MN.

则∠NMD=∠NDM，∠NMC=∠NCM.

由BC∥MN∥AD，

得∠NMD=∠ADM，∠NMC=∠BCM.

则∠ADM=∠NDM，∠NCM=∠BCM.

又∠ADC+∠BCD=180°，

则∠MDC+∠MCD=90°.

则∠DMC=90°.

即DM⊥CM.

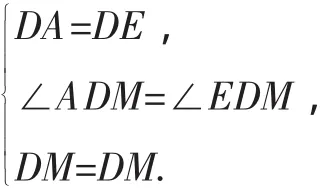
则△DAM≌△DEM（SAS）.

则∠MAD=∠DEM=90°.

即ME⊥DC.

点评：探究直角梯形中“上、下两底之和等于斜腰”时，梯形中三种线段的“垂直”美值得欣赏：一种是斜腰的两端点与直角腰中点的连线段互相垂直；一种是直角腰两端点与分斜腰使所得两部分分别等于上、下两底的点的连线段互相垂直；一种是分斜腰使所得两部分分别等于上、下两底的点与直角腰中点的连线段垂直于斜腰.

二、探究“上、下两底之和等于直角腰”的直角梯形中的“垂直”美

探究2 如图3，将探究1中的条件“AD+BC=DC”改为“AD+BC=AB”.

（1）在线段DC上是否存在一个点E，使得AE⊥BE？若存在，请找出并证明；若不存在，请说明理由.

（2）在线段AB上是否存在两点P、Q，使得DP⊥CP、DQ⊥CQ？若存在，请找出并证明；若不存在，请说明理由.

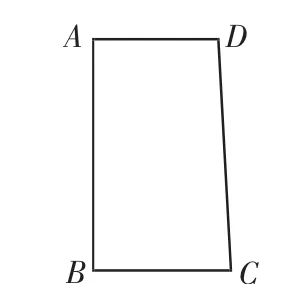
图3

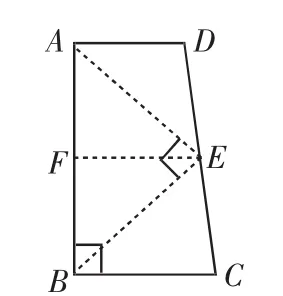
图4

解析：（1）存在.

如图4，取线段DC的中点E，连接AE、BE，此时，AE⊥BE.证明如下.

则EF=AF=BF.

则∠FAE=∠FEA，∠FBE=∠FEB.

由BC∥FE∥AD，得∠FEA=∠DAE，∠FEB=∠CBE.

则∠DAE=∠FAE=45°，∠FBE=∠CBE=45°.

则∠FAE+∠EBF=90°.

则∠AEB=90°.

即AE⊥BE.

（2）存在.

如图5，在线段AB上截取AP=BC，则AD=BP，连接DP、CP，此时，DP⊥CP.证明如下.

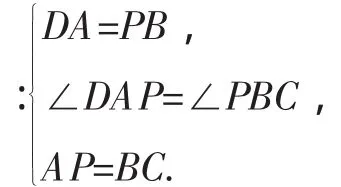
则△DAP≌△PBC（SAS）.

则∠APD=∠BCP.

由于∠BCP+∠BPC=90°，则∠APD+∠BPC=90°.

则∠DPC=90°.

即DP⊥CP.

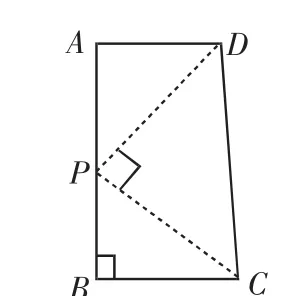
图5

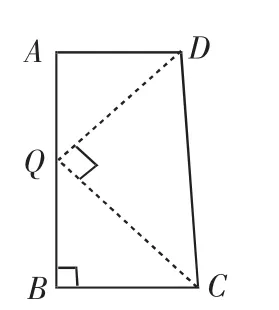
图6

如图6，在线段AB上截取AQ=AD，则BC=BQ，连接DQ、CQ，此时，DQ⊥CQ.证明如下.

∠AQD=∠ADQ=45°，∠BQC=∠BCQ=45°.

则∠DQC=90°.

即DQ⊥CQ.

点评：探究直角梯形中“上、下两底之和等于直角腰”时，梯形中也有两种线段的“垂直”美值得欣赏：一种是直角腰两端点与斜腰中点的连线段互相垂直；一种是斜腰两端点与分直角腰使所得两部分分别等于上、下两底的点的连线段互相垂直，且满足条件的点在直角腰上有两个.

1.朱光洪.斜腰等于两底之和的直角梯形与辅助圆［J］.中学数学教学参考（中旬），2005（6）.