汽车发电机的可靠性建模与分析
周 ,张奇峰
(1.同济大学汽车学院,上海 201804;2.上海法雷奥汽车电器系统公司,上海 201203)
车载交流发电机是现代汽车必不可少的组成部分,作为汽车的主要电源装置,发电机的主要功用是在保证仪表、车灯、空调及其他车载电器的用电需求的同时,及时对蓄电池进行充电,以补充蓄电池在前期使用中所消耗的电能.随着人们对汽车的舒适安全、节能环保等方面的要求越来越高,主机厂对汽车发电机的设计可靠性和工作寿命也提出了更为严格的要求,因为离开了发电机的可靠运转,汽车的先进性、舒适性等无从谈起.
如何系统地评估、预测和指导汽车发电机的可靠性设计,已成为行业重点关注的课题.本文将根据应用最为广泛的整体式交流发电机的结构原理,建立汽车发电机的可靠性模型,并提出其可靠性指标的评估方法,为今后不断提高汽车发电机的可靠性水平和质量水平建立科学依据.
1 交流发电机的结构原理
如图1所示,整体式交流发电机一般由定子、转子、前盖(前轴承)、后盖整流桥(后轴承)和调节器5部分组成.
发电机的三相定子绕组按照一定规律均布在发电机定子槽中,彼此相差120°;转子由6~8对爪极和中心励磁线圈组成.当转子在皮带轮的带动下旋转时,产生旋转磁场并切割定子中的绕组线圈,所以在定子三相绕组中产生频率相同、幅值相等、相位相差120°的三相电动势,交流电经定子绕线引入由整流二极管组成的桥式电路中,经全波整流后将直流电输出给车辆的电池-电器电路中,供车辆使用.由此可见从皮带轮、前后轴承、定转子绕组到后盖整流电路和调压电路,这一系列零部件任何一个产生失效都会造成发电机的故障.
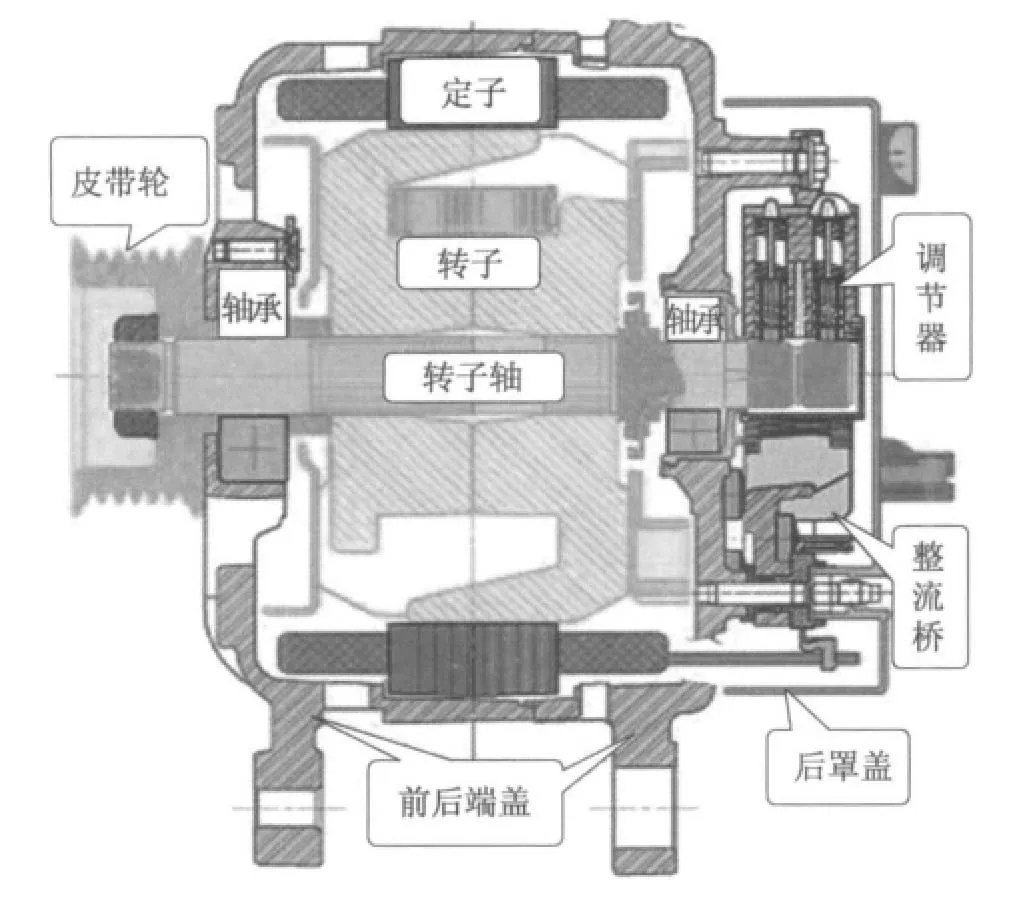
图1 交流发电机结构图Fig.1 Alternator structure profile
2 汽车交流发电机的可靠性建模
可靠性模型是指为预计或估算产品的可靠性所建立的可靠性逻辑图及其数学模型.可靠性模型包括基本可靠性模型和任务可靠性模型.基本可靠性模型是一个全串联模型,包括一个可靠性框图及有关的可靠性数学模型,它用以估计产品及其组成单元引起的维修及后勤保障要求.任务可靠性模型是一种用来描述产品在执行任务过程中完成其规定功能能力的模型,包括一个可靠性框图及其有关的可靠性数学模型,它反映在执行任务期间完成任务的能力.本文的可靠性模型指的是任务可靠性模型.
为建立汽车交流发电机可靠性模型,作如下假设:
(1)电机本体与整流控制电路都只有两种状态:故障状态和正常状态.
(2)各部件的故障是相互独立的.由文献[6]中对发电机故障树的定量分析可知,影响发电机可靠性的主要组件为电机轴承、定转子绝缘、整流电路和调节器控制电路.其中,轴承故障占49.4%,整流电路故障占24.7%,绕组绝缘故障占12.3%,调节器电路故障占4.6%,累计占总故障数的91%.以上任何一个部件出现故障,电机均不能正常工作,因此,可以把交流发电机可靠性框图简化为如图2所示的可靠性串联系统.

图2 交流发电机可靠性框图Fig.2 Alternator reliability diagram
2.1 电机轴承系统可靠性模型
发电机的轴承系统由2个轴承组成,任何1个轴承出现故障,轴承系统均不能正常工作,所以,电机轴承系统为可靠性串联系统,其可靠性框图如图3所示.图3中R1i(i=1,2)表示对应轴承的可靠度.

图3 发电机轴承可靠性框图Fig.3 Alternator bearing reliability diagram
一般认为,轴承的失效分布服从二参数威布尔分布,目前国内外的轴承行业基本上都采用这种分布,所以轴承的可靠度R1i为
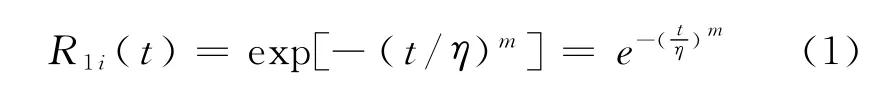
式中:t为轴承工作时间;η为轴承的特征寿命,η与电机转速、负载和轴承质量等级有关,可通过轴承的寿命模型计算获得;m为轴承失效分布的形状参数,对于球轴承m=10/9,圆柱滚子轴承m=3/2,圆锥滚子轴承m=4/3.
影响轴承寿命的因素有很多,如负载、转速、可靠度要求、润滑、轴承材料、安装精度、温度等.根据近年来对滚动轴承寿命影响因素的研究成果,可用下式来计算滚动轴承的寿命:

式中:LR为可靠度为R时的轴承寿命;n为轴承的转速;C为滚动轴承额定动负荷;fP为载荷系数;P为滚动轴承承受的当量动负荷;ε为寿命指数,球轴承为3,圆柱滚子轴承为10/3;fR为可靠度的寿命修正系数;fL为引入润滑的寿命修正系数;fG为润滑过滤精度的寿命修正系数;fS为润滑油中含水的寿命修正系数;fY为非金属含量的寿命修正系数;fH为轴承材料表面硬度减低对寿命的影响系数;fT为温度的寿命修正系数;fE为轴向偏斜的修正系数.
由式(2)计算可靠度为0.618的轴承寿命,可获得轴承的特征寿命,从而获得轴承的可靠度.由轴承系统的可靠性框图可得,其可靠度R1(t)为

式中:η1,η2分别为2个轴承的特征寿命;m1,m2分别为2个轴承的形状参数.
2.2 电机绝缘系统可靠性模型
电机绝缘系统包括匝间绝缘、槽绝缘(对地绝缘)和相间绝缘.任何一种绝缘出现故障,绝缘系统都不能正常工作.因此,电机绝缘系统为可靠性串联系统,其可靠性框图如图4所示,R21,R22,R23对应相应绝缘的可靠度.

图4 发电机绝缘系统可靠性框图Fig.4 Alternator insulation system reliability diagram
绕组绝缘近似服从威布尔分布,其分布参数与温度、绕组线径、绝缘等级、工艺、引线焊接材料等有关,需由现场使用数据或可靠性试验数据统计得出.在可靠性预计时,一般没有这些参数的数据,因此,在文献[1]中,为了简化预计,认为绕组绝缘近似服从指数分布,即电机绝缘系统可靠度R2(t)=exp(-λ2t),绕组绝缘工作失效率模型为

式中:λ2为绕组绝缘失效率;λb为基本失效率;πE为环境系数;πQ为质量系数;πC为结构系数;πK为种类系数.这些参数可以从文献[3]中查到.λb的模型为

式中:A为失效调整系数;THS为热点温度;NT为温度常数;G为加速常数.
NT,G,A可查文献[3]得到,THS可由环境温度加温升得到.由前面电机绝缘系统的可靠性模型可得电机绝缘系统的可靠度R2(t)为

式中:λ2i为相应绝缘系统的失效率.
2.3 整流电路系统可靠性模型
发电机整流电路通常由3个正向二极管 和3各个负向二极管正负串联后再并联而成.任何一个组件发生失效,都会造成整流电路和电机的失效.6个二极管均为大功率半导体组件,其寿命近似服从指数分布,所以整流电路的可靠度R3(t)为

式中:λ3i为齐纳二极管的失效率,可查阅文献[3]得到.
2.4 发电机电压调节控制电路
发电机电压调节控制电路由半导体集成芯片封装制成,集成电路的寿命同样服从指数分布,其工作失效率λ4的模型为
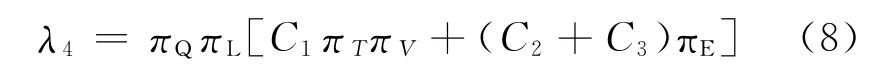
式中:πL为元器件成熟系数;πV为电压应力系数;πT为温度应力系数;C1和C2为电路复杂度失效率;C3为封装复杂的失效率.
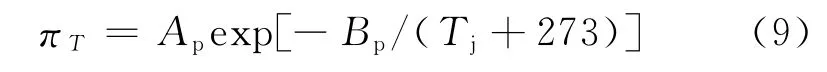
式中:Ap,Bp为组件工艺调整系数,取决于电路工艺,可查文献[3]可得;Tj为电路处于最恶劣状态时的结温.
所以电压调节器的可靠度R4(t)为

综上所述,汽车交流发电机系统的可靠度R(t)的函数模型为

汽车交流发电机系统为一个可修复系统,则系统的平均寿命(Mean Time Between Failure,MTBF)H为:

综合前面的分析可知,汽车交流电机的寿命分布服从指数分布与威布尔分布组合而成的复合型分布.这就与一般假定电机服从指数分布不同,从而否定了将传统的电机可靠性设计和可靠性试验方法应用于汽车发电机的可能性.进而进行汽车发电机设计和可靠性评估时,就不能按照寿命分布服从单一的指数分布进行,而需根据寿命分布服从指数分布与威布尔分布组合而成的复合型分布的特征进行电机的可靠性设计和评估.
3 汽车交流发电机的可靠性预计
3.1 可靠性预计概述
可靠性预计是产品在研制和开发阶段用定性和定量的方法评价系统或设备的可靠性.在研制开发阶段进行可靠性预计的意义在于:①通过可靠性预计,选择最佳设计方案;②发现可靠性薄弱环节和潜在问题;③为可靠性分配提供依据;④节省研制费用和时间,降低成本.
预计的程序是,首先确定基础件的可靠性,进而预计出部件的可靠性,以后逐级进行,最后预计出系统的可靠性.
根据设计的不同阶段,对电子电气设备可以采用不同的可靠性预计方法:在早期权衡研究和方案设计阶段采用相似设备法、相似电路法、有源部件法等方法预计可靠性;在早期设计阶段采用元器件计数法和粗略应力分析法;详细设计阶段采用应力分析法.
事实上,构成交流发电机的各单元失效率、可靠性与工作应力是密切相关的,应力分析法考虑了工作应力的影响和各单元的寿命分布类型.接下来将采用应力分析法,根据组成系统的组件、部件和子系统的可靠性,来推测系统的可靠性.对其进行可靠性预计,获得一些可靠性指标,以验证可靠性模型的实效性.
3.2 应力分析法预计发电机可靠性
如前所述,汽车交流发电机的失效主要表现为轴承失效、绕阻绝缘失效和整流控制电路失效3个方面,且可靠性模型为串联模型,下面仅考虑这3种失效模式.基于前面建立的汽车交流发电机系统的可靠性模型,以某车型的交流发电机为例,下面预计该电机的工作环境温度为105℃时的可靠性,以下计算失效率单位均为10-6次·h-1,时间t单位为106h.
3.2.1 轴承系统的可靠度R1(t)
本章前一节介绍过,轴承的失效分布服从二参数威布尔分布,目前国内外的轴承行业基本上都采用这种分布.用式(1)计算轴承的可靠度.
发电机前轴承采用的是6 303型深沟球轴承,电机工作额定转速为n=6 000r·min-1,轴承额定动负荷P1=14 300N,当量动负荷P=1 000N;质量因子fm=1.5,载荷系数fP=1,可靠度修正系数fR=1,深沟球轴承为寿命指数ε=3,计算可靠度R=0.9时的寿命得


发电机后轴承采用的是6202型深沟球轴承,电机工作额定转速为n=6 000r·min-1,后轴承额定动负荷P1=7 600N,当量动负荷P=210N,质量因子fQ=1.5,载荷系数fP=1,可靠度修正系数fR=1,计算可得η2=1.872 8.所以轴承系统的可靠度为


3.2.2 电机绕组绝缘系统的可靠度R2(t)
绕组绝缘采用H级绝缘材料,漆包线绝缘等级为F级.经温升计算的热点温度为25+125=150℃,查文献[3]中相应表得:基本失效率λb=0.041;环境系数πE=5;质量系数πQ=1;种类系数πK=1;结构系数πC=1.则绕组绝缘工作失效率为
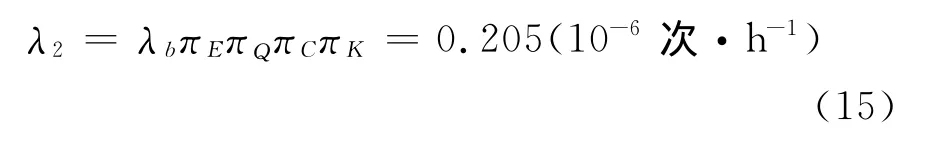
可得绕组绝缘可靠度为

3.2.3 整流电路的可靠度R3(t)
发电机整流电路通常由3个正向二极管和3个负向二极管正负串联后再并联而成.任何一个组件发生失效,都会造成整流电路和电机的失效.6个二极管均为大功率半导体组件,其寿命近似服从指数分布,所以整流电路其可靠度的计算如下:
发电机的整流二极管为齐纳二极管,查文献[3]中表可知:基本失效率λb=0.006,环境系数πE=1,质量系数πQ=1,应用系数πA=1.2,则整流二极管的工作失效率

可得整流桥的可靠度为
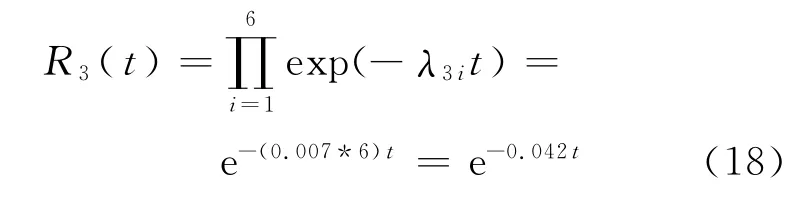
3.2.4 调节器电路的可靠度R4(t)
发电机电压调节控制电路由半导体集成芯片封装制成,芯片电路为金属氧化物半导体(MOS)模拟电路,芯片封装工艺采用密封的金属壳封装,查文献[3]的中相应参数:环境系数πE=1,质量系数πQ=0.25,成熟度系数πL=1,πQ=1,C1=0.064,C2=0.01,C3=0.08,Tj=120℃,πT=10.6,代入根据式(10)计算可得λ4=0.174.
所以调节器电路的可靠度为

由以上可靠性模型计算可得,该交流发电机系统的可靠度为

所以系统的平均无故障工作时间H为

参考国内交通部门的监控数据可知,目前国内城市道路车辆行驶的平均时速约为40km·h-1,高速公路车辆行驶的平均时速约为100km·h-1.参考汽车行业对于普通轿车的调查数据可知,轿车的日常城市公路驾驶与高速公路驾驶的里程比约为2∶1,按照目前国内汽车企业公布的整车质保期普遍为(2a,6万km)来估算,汽车发电机在质保期的工作时间为
城市公路行驶时间:(60 000×2/3)/40=1 000h,
高速公路行驶时间:(60 000×1/3)/100=200h,共计为1 200h(相当于车辆平均每天工作1.7~2.5h).
所以这里取t=0.001 2×106h代入上文建立的可靠度函数模型,可求得上述汽车交流发电机在平均无故障工作时间为1 200h的可靠度为
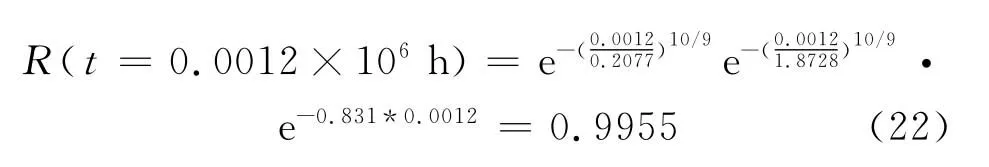
如果设计标准要求电机在此工况下的设计可靠度R=0.99,代入式(21)模型可得相应的平均寿命H=2 500h.
4 结束语
根据前文所述的里程折算方法,可以换算得出本文研究的交流发电机在可靠度R=0.99的平均无故障工作里程约为125 000km.对于家庭用户来说,99%的车辆在5~6a内不用更换和维修发电机.此可靠度水平与文献[6]中根据交流发电机故障树模型和实际的售后统计数据计算所得可靠度数值基本一致.由此可见本文的汽车交流发电机可靠度函数模型是比较符合实际的,其中的研究方法和数学模型具有推广价值.
[1]黄洪剑.航天电机可靠性及加速寿命试验研究[M].杭州:浙江大学出版社,2001.
HUANG Hongjian.Research on aerospace motor reliability and aaccelerated life test[M].Hangzhou:Zhejiang University Press,2001.
[2]王宵锋.汽车可靠性工程基础[M].北京:清华大学出版社,2007.
WANG Xiaofeng.Automobile reliability engineering[M].Beijing:Tsinghua University Press,2007.
[3]杨家铿,李红彬.电子设备可靠性预计手册[M].北京:电子工业出版社,1998.
YANG Jiakeng.LI Hongbin,Reliability prediction handbook for electronic equipment[M].Beijing:Electronic Industry Press,1998.
[4]电机工程手册编辑委员会.电机工程手册[M].北京:机械工业出版社,1997.1.
Electrical Engineering Handbook Editorial Board.Electrical engineering handbook [M].Beijing:China Machine Press,1997.
[5]斯凯孚集团.SKF轴承使用手册[M].Goteborg:SKF,2004.
SKF Group.SKF bearing user manual[M].Goteborg:SKF,2004.
[6]张奇峰.汽车交流发电机可靠性研究[D].上海:同济大学,2012.
ZHANG Qifeng.Research on reliability of automobile alternator[D].Shanghai:Tongji University,2012.

