基于RIPless理论的稀疏微波成像波形分析方法
赵 曜* 张冰尘 洪 文 吴一戎
基于RIPless理论的稀疏微波成像波形分析方法
赵 曜张冰尘 洪 文 吴一戎
(中国科学院电子学研究所微波成像技术重点实验室 北京 100190) (中国科学院电子学研究所 北京 100190)
稀疏微波成像回波数据可以建模为Toeplitz矩阵与地面场景的乘积,Toeplitz矩阵中的行向量为发射信号的时延。由于难于验证Toeplitz矩阵是否符合经典的稀疏信号处理中RIP等重建条件,因而分析稀疏微波成像采样数与发射波形的关系十分困难。近年提出的RIPless理论表明如果矩阵的行向量是对一个概率分布的随机抽取,并且该概率分布满足一定的条件,那么可以从少量的采样数据中恢复稀疏信号。Toeplitz矩阵适用于RIPless理论。该文首先介绍稀疏微波成像中观测矩阵的构造,然后利用稀疏信号处理中的RIPless理论分析波形中信号脉宽、带宽和信号形式与稀疏微波成像采样数的关系,进而比较不同波形对稀疏微波成像中的性能,最后通过仿真验证了该方法的有效性。
稀疏微波成像;RIPless;压缩感知;波形分析
1 引言
将稀疏信号处理引入微波成像技术,两者有机结合形成的微波成像新理论、新体制和新方法称为稀疏微波成像。稀疏微波成像利用场景的稀疏性先验知识,通过少量观测数据对场景进行重建。相比于传统微波成像,稀疏微波成像可以减少数据量和系统复杂度。
稀疏微波成像中的观测矩阵是指将地面场景映射为回波数据的变化矩阵,它与雷达系统密切相关。观测矩阵的性质决定稀疏微波成像的性能。稀疏微波成像中条带式合成孔径雷达回波为地面场景和发射波形的卷积,观测矩阵即是Toeplitz矩阵。矩阵的每一行是发射波形的时移。良好的发射波形设计可以提高观测矩阵的性质以减少采样数。
在稀疏信号处理中,针对观测矩阵已经提出许多评判准则,例如,限制等距条件(Restricted Isometry Property, RIP),限制正交条件(Restricted Orthogonality Property, ROP),精确重建条件(Exact Reconstruction Criteria, ERC)和互相关条件(Mutual Coherence, MC), RIP, ROP, ERC评判准则都非常难于计算,而MC条件估计的结果并不精确,许多矩阵不满足MC条件,实际上仍可以稀疏重建。稀疏信号处理中常用的观测矩阵为傅里叶矩阵或者随机矩阵,以上评判准则都难以直接应用于Toeplitz矩阵,进而难以在稀疏微波成像条带式合成孔径雷达中发挥作用。
最近Candes提出的RIPless理论,将压缩感知理论推广到更平凡的条件,如果观测矩阵中的行向量是对一个概率分布的随机独立抽取,并且该概率分布满足完备性条件和不相干条件,则可以利用少量观测数据恢复稀疏信号。与RIP相比,RIPless所要求的重建条件易于验证并且理论界更优。例如对于傅里叶矩阵,RIP要求采样数为,而RIPless所要求的采样数为,其中为被观测信号非零元素个数,为被观测信号长度。RIPless理论可以保证随机矩阵、正交矩阵等符合稀疏重建的要求,并且该理论还可对Toeplitz矩阵形式的观测矩阵恢复性能进行分析。由于条带成像雷达的观测矩阵通常为Toeplitz矩阵,可以利用RIPless理论分析不同波形构成的观测矩阵性质。本文基于RIPless理论分析发射信号脉宽、带宽和信号形式对观测矩阵的影响,进而比较不同波形对稀疏微波成像中的性能。
现在出现了许多稀疏信号处理与雷达相结合的应用。正交频分复用(OFDM)信号、随机噪声信号、Alltop波形都可以应用于稀疏微波成像中。目前这些应用大多基于实验方法分析其性能,例如相变图方法,在理论方面尚缺乏全面的分析。文献[9]利用MC比较了Alltop波形和Chirp信号在稀疏微波成像中的性能。文献[14]利用RIP分析了伪随机信号在探地雷达中的应用。由于聚束式SAR和ISAR中的观测矩阵为傅里叶矩阵,傅里叶矩阵满足RIP条件,因而稀疏信号处理可以应用于聚束式SAR和ISAR。目前难以从理论分析波形对稀疏微波成像条带式合成孔径雷达模式中的影响。
本文的结构如下。第2节介绍压缩感知中的RIPless理论,第3节介绍稀疏微波成像中观测矩阵的构造。第4节利用RIPless进行了波形分析和仿真。第5节给出了结论。
2 RIPless理论[7,8]
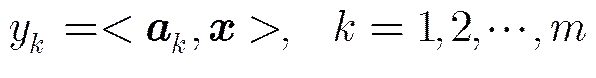
(1)


其中是一个常数,则最优化式(1)的解具有唯一性,并且以的概率等于。
3 稀疏微波成像模型[2]
合成孔径雷达是遥感中微波成像的重要技术。本文考虑条带式SAR成像模式,飞机沿直线飞行(方位向),天线以垂直于飞行方向(距离向)发射脉冲。对于观测场景,回波数据可以表示为:
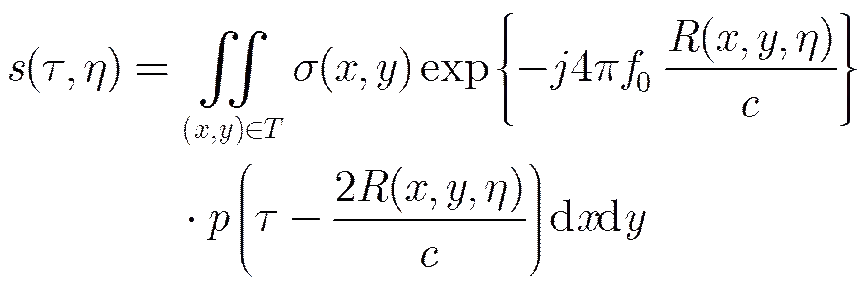
(4)
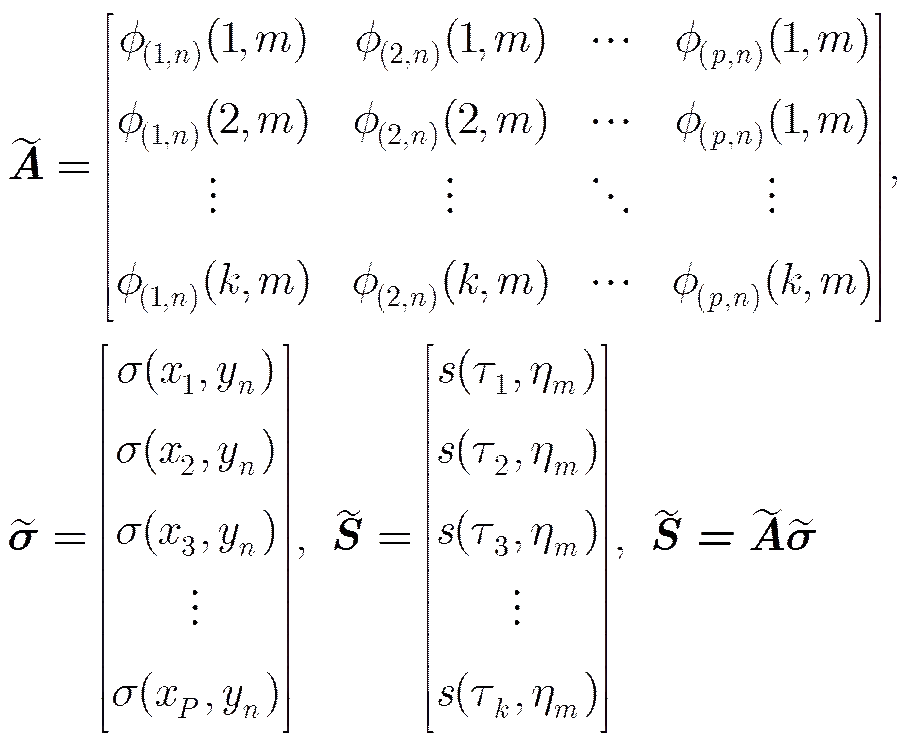
其中
4 仿真和分析
发射波形是雷达中的关键问题,影响波形的主要因素有脉宽、带宽和信号形式等。设计良好的波形可以提高观测矩阵的性质,进而提高稀疏微波成像的性能。本节由RIPless理论计算观测矩阵的条件数和不相干参数的乘积,比较不同波形在稀疏微波成像中的性能。
一般来说,SAR成像算法包括两个部分:距离压缩和方位压缩。因为两个方向的处理方法类似,所以这里只分析1维信号形式。以下将逐一分析脉宽,带宽和信号形式所产生的影响。
4.1 脉宽
本小节分析不同发射信号脉宽对于稀疏微波成像性能的影响。本小节仿真参数如下:观测距离为100 km,载频为1 GHz,信号形式为线性调频信号,带宽为100 MHz。本仿真改变脉宽大小,比较观测矩阵条件数和不相干参数的变化。图1给出了观测矩阵条件数和不相干参数及两者乘积随脉宽变化的曲线。可以看出不相干参数随着脉宽的增大而逐渐减小(如图1(a)),而条件数基本保持不变(如图1(b))。在观测矩阵中,发射信号的脉宽越大,行向量中的非零元素个数越多,所以非相干参数就越小,而条件数与雷达点扩展函数密切相关,带宽不变所以条件数基本相等。脉宽为0.5 µs和1.1 µs的仿真结果如图2所示。仿真中对两组数据同时进行25%降采样,可以发现当脉宽为0.5 µs时成像失败,成像结果中出现了许多虚假目标,而当脉宽为1.1 µs时成像成功,每个目标都得到正确重建。该仿真没有考虑噪声的影响。综上,如图1(c)所示随脉宽增大而减少,即随脉宽增大稀疏微波成像所需的采样数减少。
4.2 带宽
本节中分析不同带宽对观测数量的影响。本小节仿真参数如下:观测距离为100 km,载频为1 GHz,信号形式为线性调频信号,脉宽为1 µs。

图1 及-脉宽曲线

图2 不同脉宽下仿真结果
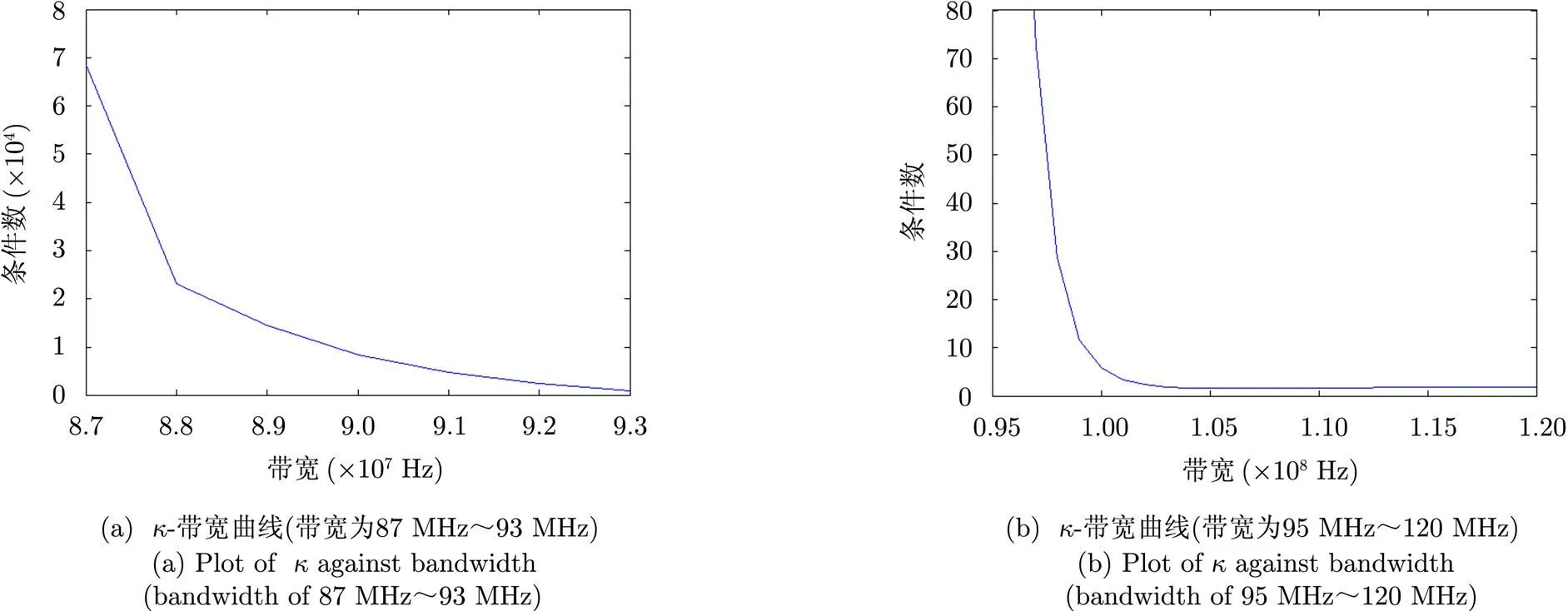
图3 -带宽曲线

图4 -带宽曲线
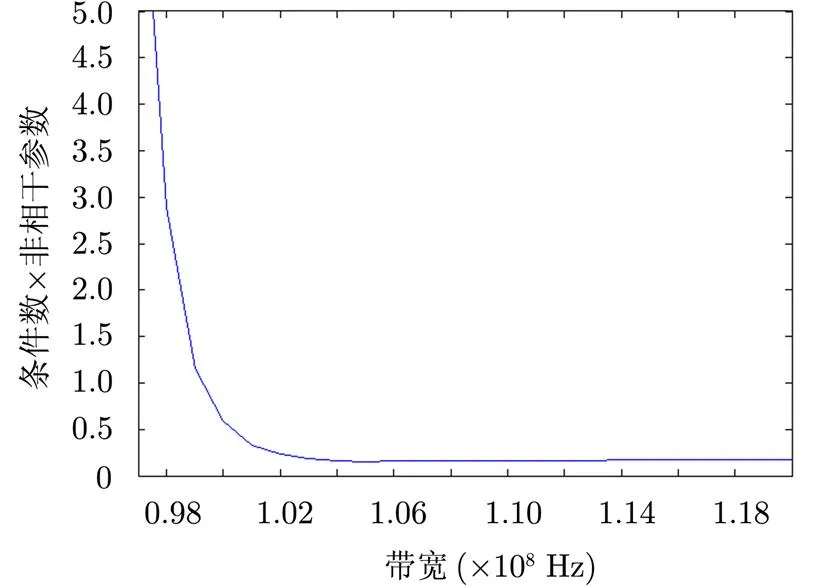
图5 -带宽曲线
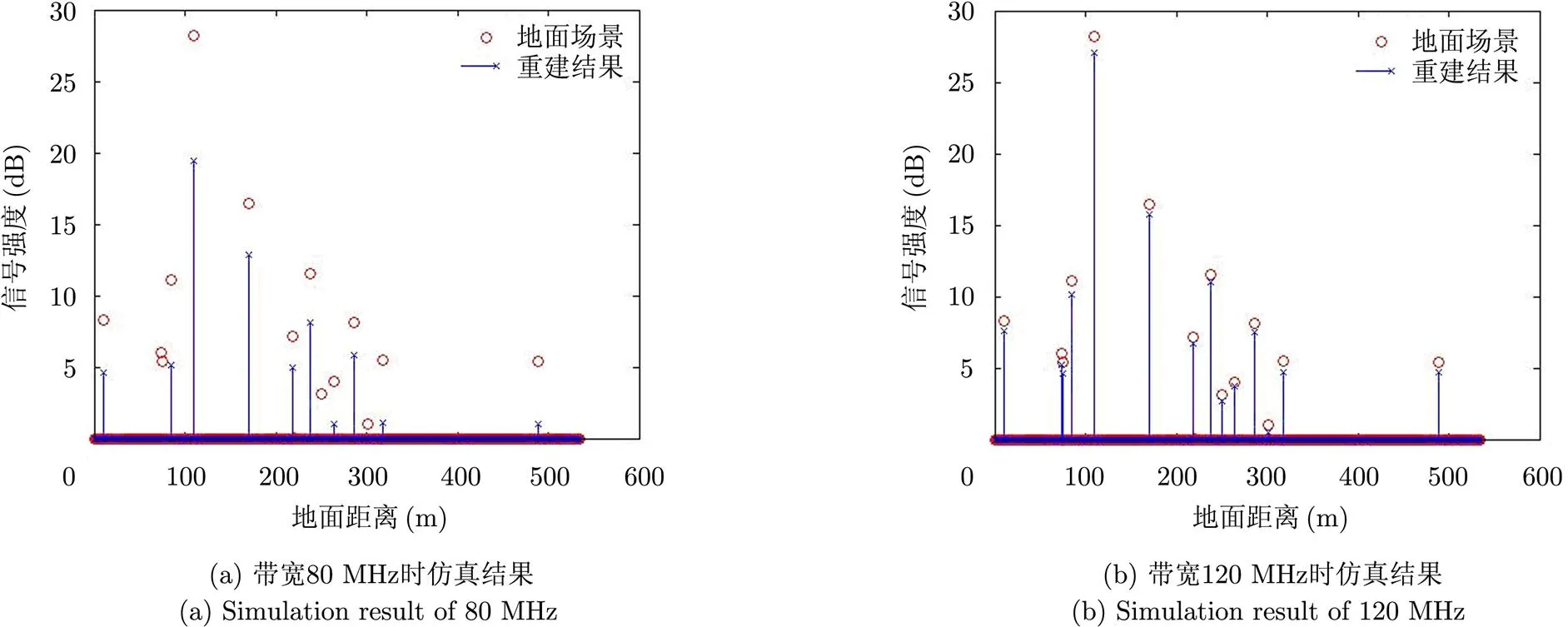
图6 不同带宽下仿真结果
4.3 信号形式
本节分析信号形式对观测数量的影响。本小节仿真参数如下:观测距离为100 km,载频为1 GHz,带宽为100 MHz,脉宽为1 µs。这里考虑3种信号形式线性调频信号、随机噪声信号和正交频分复用(OFDM)信号。线性调频信号具有良好的匹配滤波性质和抗多普勒偏移性质,在雷达中有广泛应用。由于随机噪声信号构建的观测矩阵具有良好的列不相关性,非常适宜稀疏微波成像应用。OFDM信号的频谱与随机噪声信号类似,也可以应用于稀疏微波成像。表1给出了3种波形所构建的观测矩阵的条件数、非相干参数及两者乘积。可以看出观测矩阵的条件数和非相干参数3种发射信号基本相等,相比而言,随机噪声信号最优,OFDM次之,线性调频信号再次之。综上,在稀疏微波成像中随机噪声信号和OFDM信号的性质略优于线性调频信号,不过它们三者之间的差异并不大。该结果与文献[13]中相变图分析结果一致。
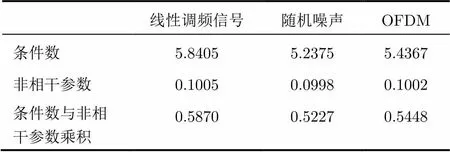
表1 3种信号形式的条件数、非相干参数及两者乘积
5 结论
RIPless理论适用于稀疏微波成像观测矩阵的分析,通过RIPless理论可以比较稀疏微波成像发射波形对成像性能的影响。目前采用仿真方法分析了发射信号脉宽、带宽和信号形式、采样数对图像重建效果的影响。如何直接建立发射信号与RIPless理论中条件数与非相干参数之间的理论关系需要进一步研究。
[1] Donoho D. Compressed sensing[J]., 2006, 52(4): 1289-1306.
[2] Zhang Bingchen, Hong Wen, and Wu Yirong. Sparse microwave imaging: principles and applications[J]., 2012, 55(8): 1722-1754.
[3] Candes E, Romberg J, and Tao T. Stable signal recovery from incomplete and inaccurate measurements[J]., 2006, 59(8): 1207-1223.
[4] Candes E and Tao T. Decoding by linear programming[J]., 2005, 51(12): 4203-4215.
[5] Tropp J. Greed is good: algorithmic results for sparse approximation[J]., 2004, 50(10): 2231-2242.
[6] Ben-Haim Z, Eldar Y C, and Elad M. Coherence-based performance guarantees for estimating a sparse vector under random noise[J]., 2010, 58(10): 5030–5043.
[7] Candes E and Plan Y. A probabilistic and RIPless theory of compressed sensing[J]., 2011, 57(11): 7235-7254.
[8] Kueng R and Gross D. RIPless compressed sensing from anisotropic measurements[J]., 2013, http://dx.doi.org/10.1016/j.laa.2013.04.018.
[9] Herman M and Strohmer T. High-resolution radar via compressed sensing[J]., 2009, 57(6): 2275-2284.
[10] Jiang Hai, Zhang Bingchen, Lin Yueguan,.. Random noise SAR based on compressed sensing[C]. Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, July 25-30, 2010: 4624-4627.
[11] Berger C, Demissie B, Heckenbach J,.. Signal processing for passive radar using OFDM waveforms[J]., 2010, 4(1): 226-238.
[12] Tian Ye, Jiang Chenglong, Lin Yueguan,.. An evaluation method for sparse microwave imaging radar system using phase diagrams[C]. Proceedings of CIE Radar Conference, Chengdu, China, 2011: 210-213.
[13] Zhang Zhe, Zhang Bingchen, Hong Wen,.. Waveform design forLregularization based radar imaging and an approach to radar imaging with non-moving platform[C]. 9th European Conference on Synthetic Aperture Radar (EUSAR), Nuremberg, Germany, April 23-26, 2012: 685-688.
[14] Xu X, Wang W, Lin Z,.. Pseudo random binary sequence GPR imaging via compressive sensing[C]. Session 2P7, 405.
[15] Patel V M, Easley G R, Healy D M,.. Compressed sensing for synthetic aperture radar imaging[C]. 2009 16th IEEE International Conference on Image Processing (ICIP), November, 2009: 2141-2144.
[16] Ender J H G. On compressive sensing applied to radar[J]., 2010, 90(5): 1402-1414.
RIPless Based Radar Waveform Analysis in Sparse Microwave Imaging
Zhao Yao Zhang Bing-chen Hong Wen Wu Yi-rong
(National Key Laboratory of Science and Technology on Microwave Imaging, Beijing 100190, China) (Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China)
Echo data can be modeled as the product of the Toeplitz matrix and reflectivity of the observed scene. The row of the Toeplitz matrix is the time shift of the transmitted signal. Because it is difficult to verify whether the Toeplitz matrix satisfies the reconstruction condition (such as restricted isometry property) of sparse microwave imaging, analyzing the performance of the transmitted signal in sparse microwave imaging is a problem. RIPless, a new progress in sparse signal processing, shows that if the row of the matrix is an independent and identically distributed (i.i.d.) random vector drawn from a distribution, and this distribution satisfies certain conditions, then one can faithfully recover approximately sparse signals from a minimal number of measurements. The Toeplitz matrix satisfies RIPless. In this paper, we introduce the construction of the measurement matrix in sparse microwave imaging. Further, the relationship between pulse duration, bandwidth and waveform type, and the number of measurements in sparse microwave imaging are analyzed. The simulation results show the effectiveness of the proposed method.
Sparse microwave imaging; RIPless; Compressed sensing; Waveform analysis
TN958
A
2095-283X(2013)03-0265-06
10.3724/SP.J.1300.2013.13032
2013-03-29收到,2013-07-04改回;2013-07-10网络优先出版
国家“973”计划项目(2010CB731900)资助课题
赵曜 yaozhao@mail.ie.ac.cn
赵 曜(1984-),男,籍贯江西,北京航空航天大学博士学位,现在中国科学院电子学研究所工作,研究方向为小波分析、压缩感知、稀疏信号处理、稀疏微波成像。
E-mail: yaozhao@mail.ie.ac.cn
张冰尘(1973-),男,籍贯浙江,1996年获得中国科技大学学士学位,1999年获得中国科学院电子学研究所硕士学位,现任中国科学院电子学研究所研究员。研究方向为微波遥感与雷达技术、稀疏信号处理。
E-mail: bczhang@mail.ie.ac.cn
洪 文(1968-),女,籍贯上海,北京航空航天大学博士学位,中国科学院电子学研究所研究员。主要研究方向为合成孔径雷达成像与系统及其应用、极化/极化干涉合成孔径雷达数据处理及应用、3维微波成像新概念新体制新方法等。E-mail: whong@mail.ie.ac.cn
吴一戎(1963-),男,籍贯安徽,中国科学院院士,研究员,博士生导师,中国科学院电子学研究所所长,中国科技大学信息学院名誉院长。主要研究方向为微波成像理论研究、微波成像技术、雷达信号处理、高分辨率和干涉SAR系统技术、遥感卫星地面处理与应用系统技术等。
E-mail: wyr@mail.ie.ac.cn
——信号处理

