GPS导航电文中星历参数量化对接收机性能的影响分析

闫付龙，寇艳红，赵 昀

（北京航空航天大学 电子信息工程学院，北京 100191）

1 引言

卫星位置的精确信息是用户使用卫星导航系统实现导航定位、测速、授时等应用的关键［1］，而卫星的位置信息是以导航电文中星历参数的形式发播给用户的，星历参数的精度直接决定了用户接收机中卫星位置的计算精度，进而影响定位、测速和授时应用的性能。

就GPS系统而言，导航电文星历参数在发播前按相应ICD（Interface Control Document，接口控制文档）中规定的格式表示成二进制比特流的形式，用户接收机通过解调的导航电文比特流解码得到星历参数，星历参数由浮点数到有限字长二进制数的这一量化过程会带来一定的数值偏差，即量化前后的星历参数值不完全一致，导致卫星位置计算的偏差，从而在用户测距以至导航定位解算中引入偏差。GPS L1C信号设计任务组的成员在文献 ［2］中曾提到，在GPS NAV （Navigation）格式的电文和CNAV （Civil Navigation）格式的电文中星历参数的这种量化舍入分别可带来多达0.4m和0.03m的伪距偏差，但是这一说法并未见诸有关详细分析和实验验证的报道。出于新一代卫星导航信号电文结构设计论证的需求，本文针对NAV电文格式中星历参数量化过程及其对卫星位置计算、UERE （User Equivalent Ranging Error，用户等效距离误差）和用户接收机定位性能的影响进行了详细分析，对大量仿真的结果进行了总结；进一步通过GPS L1C/A数字中频信号模拟器和软件接收机的闭环测试结果验证了上述分析的正确性。

2 星历参数量化引入的卫星位置误差分析

本节首先基于由IGS（International GPS Service，国际GPS服务组织）网站下载的RINEX（Receiver Independent Exchange，与接收机无关的数据交换）格式的GPS L1C/A信号广播星历，举例说明电文中星历参数的量化误差带来的问题。这里取2012年4月14日0时0分0秒的广播星历，对PRN （Pseudo Random Numbers，伪随机编号）为5的卫星星历参数和对应的位置进行详细分析。其星历基准时刻toe为518400s，以平近点角M0参数为例，该广播星历中M0（量化前）为1.564 813 284 434，量化过程如下［3］

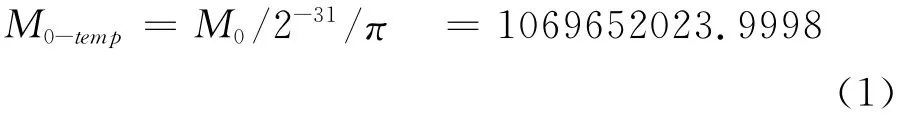
将量化后的M0－temp取整为1069652023，转换为对应的电文比特流111111110000011001100000110111，可算得量化后的M0－quantified为

则量化引入的偏差为ΔM0＝M0－quantified－M0＝－0.000000001463。

将上述广播星历中所有轨道参数量化前后数值列表表示，见表1。

可见在上述GPS广播星历的轨道参数中，只有轨道半径的正余弦调和修正项幅度Crc、Crs数值表示的后5位有效数字均为0；除Crc、Crs之外，其它轨道参数量化前后的数值均不一致。分别用量化前和量化后的两组轨道参数计算PRN5号卫星从toe时刻开始2h内的三维位置［3］，其在ECEF（Earth Centered Earth Fixed，地心地固）坐标系下的单轴偏差 （Δx，Δy，Δz）和三维偏差Δs结果如图1、图2所示。

表1 各星历参数量化前后数值对比

图1 toe时刻起2h内卫星位置单轴偏差

由以上结果分析可知，由于卫星轨道参数量化前后数值上的差异，使得所计算的卫星位置产生一定偏差。本文基于不同时段、不同卫星的星历参数进行了大量仿真分析，得出如下结论：由toe时刻开始2h内，由导航电文量化误差带来的三维卫星位置计算偏差始终保持在0.2m以内。

接下来进一步考察一周的时间段内导航电文星历参数量化过程对卫星位置计算的影响。选取上述数据的GPS周起始时刻 （toe为0s）即2012年4月8日0时0分0秒的GPS广播星历，仿真计算t＝0－604 800s的一周时间内PRN5号卫星星历参数量化前后卫星位置的偏差，结果如图3和图4所示。

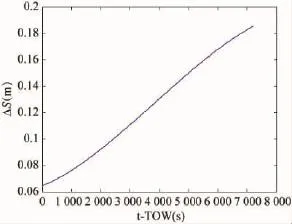
图2 toe时刻起2h内卫星位置三维偏差

图3 一周内卫星位置单轴偏差

图4 一周内卫星位置三维偏差

以上述算例为代表，大量的仿真结果表明，由星历参数量化带来的卫星位置偏差随着时间的推移呈增加趋势，且呈现周期性变化，变化周期约为12h、即1个GPS卫星轨道周期，但一周时间内卫星位置单轴偏差不超过5m。上述偏差呈现周期性变化的原因在于GPS广播星历参数是通过对GPS预报轨道拟合得到的［4］，其参数计算利用了轨道摄动的基本特征，舍去了量级较小的短周期摄动项，并将摄动因素导致的长期或长周期变化吸收到开普勒根数、轨道倾角、升交点赤经、卫星纬度角等长期变化参数中，因而基于量化前后轨道参数计算出卫星位置，其偏差的变化规律也通过GPS轨道周期反映出来。

3 基于模拟器和接收机的闭环测试

以上通过量化前后的两组星历参数计算卫星位置是基于同样的卫星信号发射时刻进行的，而在实际的用户接收机中计算卫星位置所用的历元时刻是通过接收机对所接收信号的相位状态估计值解算得到的，其与真正的卫星发射时刻时间之间存在误差。本文通过实验室自研的GPS L1C/A数字中频信号模拟器和软件接收机进行闭环测试，讨论在实际中存在历元时刻测量误差的条件下，导航电文星历参数量化对卫星位置计算的影响，以及导航电文星历参数量化误差对UERE和定位性能的影响。为了消除其它误差项对UERE计算的影响，模拟器与接收机闭环测试时关闭电离层、对流层和卫星钟差误差项。

模拟器所生成数据的配置条件如下： （1）星历选用2012年4月14日0时0分0秒的GPS广播星历；（2）用户接收机载体轨迹设为静态位置（经度30°E、纬度120°N、高程2 000m）； （3）中频频率设为1.405MHz，采样率设为5.714MHz，前端带宽设为2MHz；（4）仿真起始时刻为星历toe时刻 （周内秒518 400s），仿真时长为2h。

在模拟器中计算星历参数量化前的卫星位置，在接收机中由解调得到的星历参数 （量化后）计算卫星位置，得到PRN 5号卫星位置的偏差如图5和图6所示。

对比图1、图2与图5、图6可知，模拟器与接收机的闭环测试结果与前述仿真分析结果完全一致。大量测试结果表明，在toe时刻起2h内卫星轨道参数量化前后卫星位置的三维偏差不超过0.2m。可见其中历元时刻测量误差的影响可以忽略不计。为了更清楚地说明这一推理的正确性，本文专门针对历元时刻测量误差的影响进行以下分析和测试。

图5 闭环测得2h内卫星位置单轴偏差

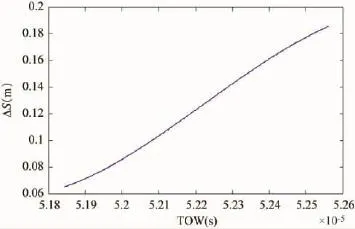
图6 闭环测得2h内卫星位置三维偏差

一般GPS接收机PVT解算得到的用户钟差一般不会超过100ns，因而模拟器和接收机闭环测试中卫星信号发射历元时刻的对准误差也在100ns以内。由于GPS卫星运动的最大速度约为3 900m/s，则由该历元时刻的对准误差导致的卫星位置误差小于0.4mm。

为了单独考察历元时刻未对准造成的卫星位置计算误差，我们在模拟器和接收机的闭环测试中采用了如下方法来消除卫星星历参数量化引起的卫星位置计算偏差：基于模拟器所生成导航电文中取出的星历参数 （即量化后的星历参数）来计算卫星位置、在模拟器中基于该卫星位置 （而非由量化前星历参数计算的卫星位置）与用户载体轨迹计算所仿真信号的状态参数，将生成的数字中频信号送入软件接收机进行捕获、跟踪、电文解调解码、卫星位置计算和PVT解算。这样的闭环测试预期可以消除卫星星历参数量化引起的卫星位置计算偏差，得到的模拟器与接收机所计算卫星的偏差如图7及图8所示。

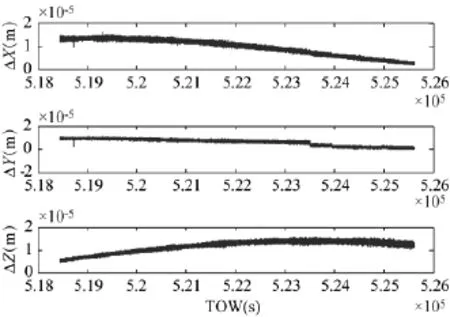
图7 消除量化误差后闭环测得2h内单轴偏差

图8 消除量化误差后闭环测得2h内三维偏差

由图7及图8可知，在消除有星历参数量化导致的卫星位置计算偏差后，由模拟器和接收机闭环测得的卫星位置计算误差不超过在从toe时刻开始2h内不超过0.022mm，这一误差主要由接收机对于卫星信号发射时刻的测量误差引起，测试结果验证了前述分析的正确性和测试方法的可行性。

4 星历参数量化误差对UERE和定位性能的影响分析

设根据量化前后的星历参数计算的某一信号发射 时刻的 卫 星位置分 别 为 （Xs1，Ys1，Zs1）和（Xs2，Ys2，Zs2），卫星位置计算偏差为Δ→S＝（Xs2－Xs1，Ys1－Ys2，Zs1－Zs2），并设用户位置为 （Xu1，Yu1，Zu1），则用户到卫星的距离为＝（Xs1－Xu1，Ys1－Yu1，Zs1－Zu1），卫星位置偏差投影在用户到卫星的视线方向上造成的UERE为

式中，θ为用户到卫星的视线方向和卫星位置矢量差方向的夹角。

图9仿真了由toe时刻开始2h内星历参数量化引起的PRN5号卫星位置计算偏差在用户到卫星视线方向上的投影结果，表3则总结了所仿真的由toe时刻开始2h内星历参数量化引起的各颗卫星位置计算偏差及相应的UERE范围。

从表3可知，在2h的星历有效时间段内由星历参数量化造成的UERE偏差不超过±0.06m；且不同卫星的位置偏差对UERE影响不同，从而会导致定位解算的偏差。图10仿真了上述条件下由星历参数量化造成的用户位置解算偏差，可见其影响不超过厘米级。

图9 星历参数量化引起的PRN5UERE

表3 星历参数量化引起的各颗卫星位置偏差及UERE范围

图10 星历参数量化引起的定位偏差

5 结论

本文仿真分析了NAV导航电文中星历参数量化对接收机性能的影响，并基于模拟器与接收机进行了闭环测试，得出如下结论：

（1）NAV电文星历参数量化导致的卫星位置计算偏差在2h的星历有效时间内不超过0.2m；

（2）NAV电文星历参数量化造成的UERE在2h的星历有效时间内不超过0.06m，引入的定位偏差在厘米级。

［1］KAPLAN E，HEGARTY C.Understanding GPS：Principles and Applications［M］.Boston：Artech House Inc.，2005：34－50.

［2］STANSELL T A，HUDNUT K W，KEEGAN R G.Future Wave L1CSignal Performance and Receiver Design［J］.GPSWorld，2011，23（6）：30－32.

［3］IS－GPS－200E，Global Positioning System Wing （GPSW）Systems Engineering ＆Integration Interface Specification［S/OL］.（2010－06－08）［2012－12－28］.http：//www.gps.gov/technical/icwg/IS－GPS－200E.pdf.

［4］崔先强，焦文海，贾晓林，等.GPS广播星历参数拟合算法［J］.测绘学院学报，2004，21（4）：244－246.

［5］IS－GPS－800，Global Positioning System Wing （GPSW）Systems Engineering ＆Integration Interface Specification［S/OL］.（2008－09－04）［2012－12－28］.http：//www.gps.gov/technical/icwg/IS－GPS－800.pdf.

［6］IS－GPS－200F，Global Positioning System Wing （GPSW）Systems Engineering ＆Integration Interface Specification［S/OL］.（2011－09－21）［2012－12－28］.http：//www.gps.gov/technical/icwg/IS－GPS－200F.pdf.