基于交并集的冲突自适应证据融合方法
汪永伟,赵荣彩,刘育楠,司 成,邱 卫
1.信息工程大学,郑州 450004
2.河南省信息安全重点实验室,郑州 450004
基于交并集的冲突自适应证据融合方法
汪永伟1,2,赵荣彩1,刘育楠1,2,司 成1,2,邱 卫1,2
1.信息工程大学,郑州 450004
2.河南省信息安全重点实验室,郑州 450004
1 引言
D-S证据理论是20世纪70年代发展起来的一种数学工具,其主要优点是:能够很好地表示“不确定”、“不知道”等重要概念,尤其在不确定表示、度量和组合方面具有优势[1-2]。基于该理论的信息融合方法能够实现空间或时间上冗余信息和互补信息的融合,获得被测对象的一致性描述,有效降低决策中的不确定性,因而在多传感器网络、信息融合、故障诊断和目标识别等领域得到广泛应用[3-8]。
Dempster组合规则是证据理论进行信息融合的有效方法。但是,当证据之间冲突程度较高时,Dempster组合规则会得出有悖于常理的结论,即Zadeh悖论[9-10]。针对此问题,国内外许多学者针对提出了许多改进方法。这些方法主要沿着两个方向展开:一是基于修正证据源的方法。首先对证据源进行评价与修正,弱化不可靠证据的影响,然后利用组合规则对证据进行融合。在此方面,Shafer、Haenni、Murphy等人提出了各自的修正方法[11-12],其中最著名的是Shafer提出的折扣法,但其易造成冲突信任向全集的扩散。二是基于修正组合规则的方法,主要思路是调整冲突信任的分配空间和分配权重,优化冲突信任分配方案。在此方面,Yager等人[13]提出了将冲突信任分配给全集命题的方法,该方法在处理低冲突证据时结果比较理想,而在高冲突环境下,由于其将冲突信任扩散到了冲突无关焦元,造成了信任分配不公平,在合成多个高冲突证据时,有一票否决的缺点。Dubois、Parade、Mihai、Yee等人[12,14-15]提出了将冲突信任进行局部分配的方法,该方法将冲突信任分配给冲突焦元的并集,分配方法较为合理,完整地保留了冲突焦元的信任信息,有效地避免了悖论问题的产生。但是,由于其对最终的融合结论未做进一步的处理,并集命题会保留较多的信任,不利于最终的决策。
分析现有的研究工作可以看出:现有的冲突证据分配方法中,都存在一定的不足,未能将证据源可靠性与组合规则改进进行统筹考虑,同时,在采用局部分配和全局分配的方法中,未能对融合结果进一步处理,融合结论的区分能力较差。Zadeh问题有可能是不可靠的证据源造成的,也可能是由于现有组合规则对冲突信任分配的不合理造成的。因此,本文提出了一种新的冲突证据融合方法。首先基于证据间的冲突关系构建冲突矩阵,并以此计算证据源的可信度,并基于可信度对证据进行折扣,减小不可靠证据对融合结果的影响;然后基于证据间的冲突程度动态调整组合规则中交集命题和并集命题的权重,以获得更为准确有效的组合结论;最后将多元素焦元的信任在单元素焦元中进行再分配,提高了信息的决策能力。
2 证据理论及其存在的不足
证据理论是建立在非空有限域Θ上的理论,Θ称为识别框架,表示有限个系统状态。证据理论使用信任函数来表示证据对每一个命题的支持程度,若命题为A,则m(A)表示命题 A的基本信任分配函数。证据理论的核心是Dempster组合规则,其可以形式化表示为:
设识别框架Θ的n个证据为{E1,E2,…,En},其对应的基本信任分配函数为mi(i=1,2,…,n),则这n个证据组合后的证据信度分配函数为:

3 基于交并集的冲突自适应证据融合方法
综合第1章的分析,现有的证据理论的改进方法主要单方面从证据源或组合规则进行考虑,且对融合结论中的多元素焦元未进行处理,改进的效果并不理想。因此,本文基于对证据理论悖论问题两种产生原因的综合考虑,提出了一种新的冲突证据融合方法。该方法将证据融合过程分为三个阶段:首先,基于证据间的冲突关系构建冲突矩阵,并以此计算证据源的可信度,并基于可信度对证据进行折扣,减小不可靠证据对融合结果的影响;其次,采用局部冲突、局部分配的原则,基于证据间的冲突程度动态调整组合规则中交集命题和并集命题的权重,以获得更为准确有效的融合结论;最后,将多元素焦元的信任在单元素焦元中进行再分配,方便了最终的信息决策。
3.1 证据可信度度量
假设n个证据构成的证据向量为 E=(E1,E2,…,En),则证据i和 j间的冲突可表示为:

kij反映的是证据i和 j之间的局部冲突度,通过累加与其他证据的冲突,可以获得证据i的全局冲突度,它反映的是其他证据对证据i冲突的支持程度。因此,证据i的冲突支持度可表示为:
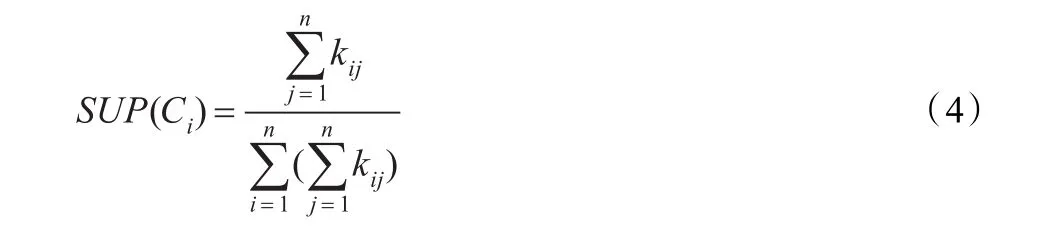
一个证据与其他证据间的冲突越小,则表明其他证据对该证据的支持程度越高,该证据的可信性越高,在证据组合时应为其分配较高的权重;反之,若一个证据与其他证据间的冲突越大,该证据的可信性越低,在证据组合时应为其分配较小的权重。SUP(Ci)从全局的视角较好地反映了证据i与其他所有证据之间的冲突关系,因此,可将其作为衡量证据重要性的参考依据。
设证据的可信度为R,则证据i的可信度ri可表示为:

式(5)中,当SUP(Ci)=0时,ri=1;SUP(Ci)=1时,ri=0。依据SUP(Ci)与ri的变化特点,可以看出,ri能够较好地反映证据的可信程度。
对于n个组合证据,采用式(2)~式(5)计算每条证据的可信度,获得证据的可信度向量 R={r1,r2,…,ri,…,rn},该向量可作为衡量证据重要性的权重向量。
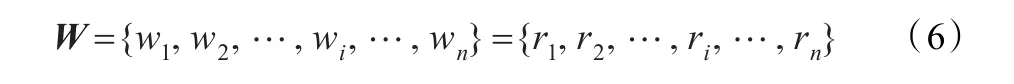
3.2 证据源修正
悖论问题的产生有可能是不可靠的证据源引起的。因此,当多证据源进行组合时,首先需要对证据的初始信任进行折扣操作[10],以降低不可靠证据对组合结论的影响,从而提高组合结论的正确性与组合方法的收敛速率。本文采用寻二辉等人提出的折扣率法[11],折扣率计算公式为:
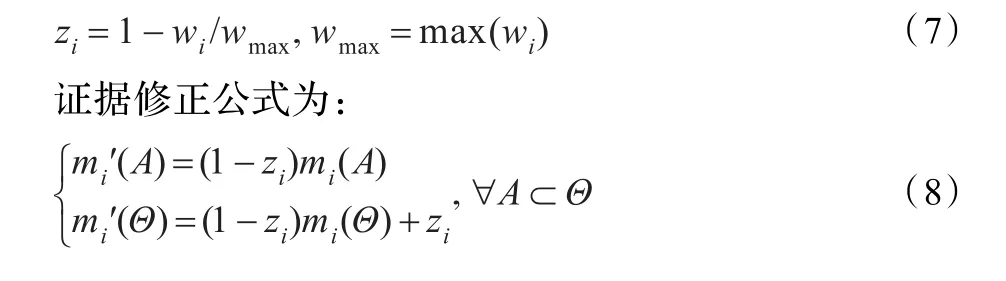
3.3 基于交并集的冲突自适应证据组合规则
现有的组合规则大致可以分为两类,一类是采用合取的方法,将冲突信任分配给冲突相关焦元的并集;另外一类是采用析取的方法,将冲突信任分配给冲突相关焦元的交集。第一类方法将冲突信任保留在并集,暂缓决策,等待更多的证据汇集后得出更为准确的结论,适合高冲突的情况;第二类方法则适合一致性较好的情况。本文将两种方法进行了综合,提出了一种基于交并集的冲突自适应证据组合方法ACCRIU(Adaptive Confliction Combination Rule based on Intersection and Union),其主要思想是如果两个证据之间的冲突较低时,采用合取规则进行合成,将冲突主要向交集命题空间进行分配;如果两个证据之间的冲突很高,采用析取规则进行合成,将冲突主要向并集命题空间进行分配。即,析取规则与合取规则的权重依据冲突k的变化而动态变化。
3.3.1 两个证据的合成规则
假设,识别框架Θ={B,C},由两个证据组成,其对应的基本信任分配函数为m1(B)和m2(C),则这两个证据组合后的证据信度分配函数如式(9)所示。

其中,α(k)应为关于k的单调递减函数,β(k)为关于k的单调递增函数。k=1时,冲突最大,将冲突全部分配给并集命题;k=0时,冲突最小,将冲突全部分配给交集命题;且析取规则与合取规则权重之和为1。即满足条件(10)、(11)和(12)。

满足公式(10)、(11)、(12)的α(k)和 β(k)都可作为合取规则与析取规则的系数,本文取:

容易证明,α(k)和β(k)满足条件(10)、(11)、(12)。
3.3.2 多个证据的合成规则
假设,识别框架Θ={E1,E2,…,En},由n个证据组成,其对应的基本信任分配函数为m1,m2,…,mn。则这n个证据组合后的证据信度分配函数如式(15)所示。

在两证据合成时,冲突等于交集为空的焦元信任乘积之和。相应地,在n个证据合成时,其冲突计算公式为:

3.4 多元素焦元信任的再分配
在实际应用中,人们需要依据单元素命题的取值进行最终的决策。为了保证决策结果的准确性,需要将多元素焦元的信任依恰当的比例分配给单元素焦元。m(A)是分配给命题A的信任,它从某种程度上代表了对命题A绝对信任程度的度量。因此,定义证据中单元素命题之间信任的比值为相对可信度。

式(17)中,δ表示单元素命题A与单元素命题B的相对可信度。依据相对可信度,则实现对合成结论中多元素焦元信任的重新再分配。分配采用等比例分配的方法,如式(18)、(19)、(20)所示。

通过对多元素焦元信任的调整,使合成结论中信任仅分布于单元素焦元,提高了融合结论的区分能力,方便了最终的决策。
4 实验仿真
为了说明本文所提出方法的有效性,利用Matlab构建仿真系统,将本文的方法与其他的证据合成方法进行了实验对比。实验中选取经典的Dempster方法以及Dubios、Mihai、Yee等典型的同类证据合成方法作为比较对象。实验设置如下。
设识别框架为Θ={A=轰炸机,B=民航客机,C=战斗机},在某一时刻利用传感器的观测信息构造的10个证据如表1所示。
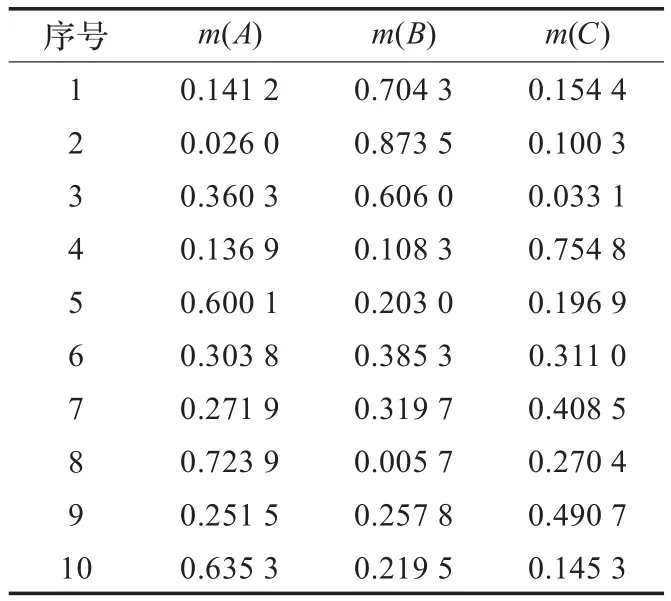
表1 原始证据表格
通过公式(6)可计算权重向量为:

利用公式(8)对原始证据进行修正,修正后的证据表格如表2所示。
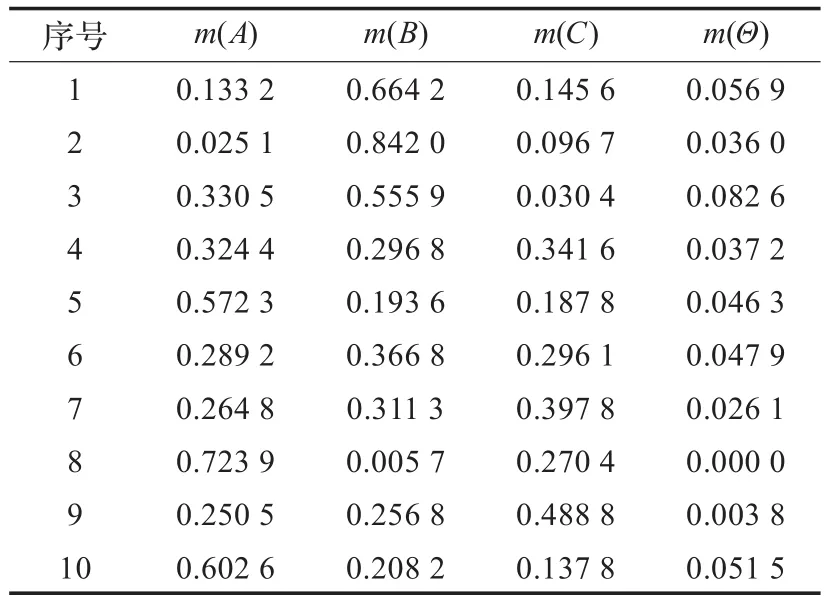
表2 修正后的证据表格
然后,分别对修正后的证据进行合成,依次取前2、3、4,10个证据进行测试,共进行9次合成运算。由于第1次测试,仅有两个证据参与合成,因此采用公式(9)进行合成,其余8次采用公式(15)进行合成,并采用公式(18)、(19)、(20)对合成结果进行信任再分配。最终得到的合成结果为:

图1~8给出了本文方法与对比方法的实验结果。
图1是证据依次加入时,新证据与其他证据的冲突变化情况。由图2至图4可以看出,Dempster组合规则无法处理高冲突的情况,在高冲突环境下(前4组证据的组合),新证据支持命题A和命题C,但Dempster仍然将冲突信任分配给命题B,出现了新证据合成失效的情况,产生了Zadeh悖论。由图2至图8可以看出,Dubois和Mihai的组合方法虽然避免了悖论问题,但由于其将冲突信任分配给了并集命题,从而导致最终的融合结果中并集所获得的信任较多,融合结论的区分能力较差。Yee方法中,将信任扩散到全集,随着证据的累加,全集所获得的信任逐步增多,最终导致无法做出明确的决策。

图1 冲突变化曲线

图2 m(A)变化曲线

图3 m(B)变化曲线
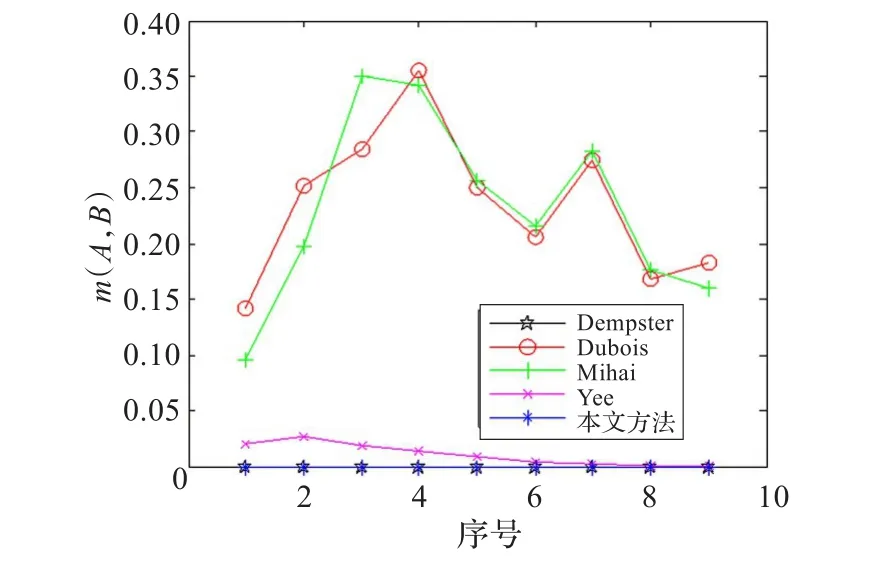
图5 m(A,B)变化曲线
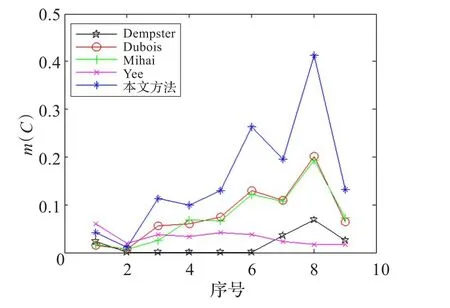
图4 m(C)变化曲线

图6 m(A,C)变化曲线
本文的方法中,由于首先利用可信度对证据进行折扣操作,降低了不可靠证据对最终结果的影响,起到了信息“过滤作用”,提高了信息收敛的速度;自适应的组合规则依据冲突变化动态调整分配权重,为冲突信任选取了合理的分配空间,避免了悖论问题的产生;对证据组合后,又对多元素焦元信任进行了调整分配,扩大了单元素焦元的信任,起到了信息“放大”作用,提高了信息的决策能力。

图7 m(B,C)变化曲线
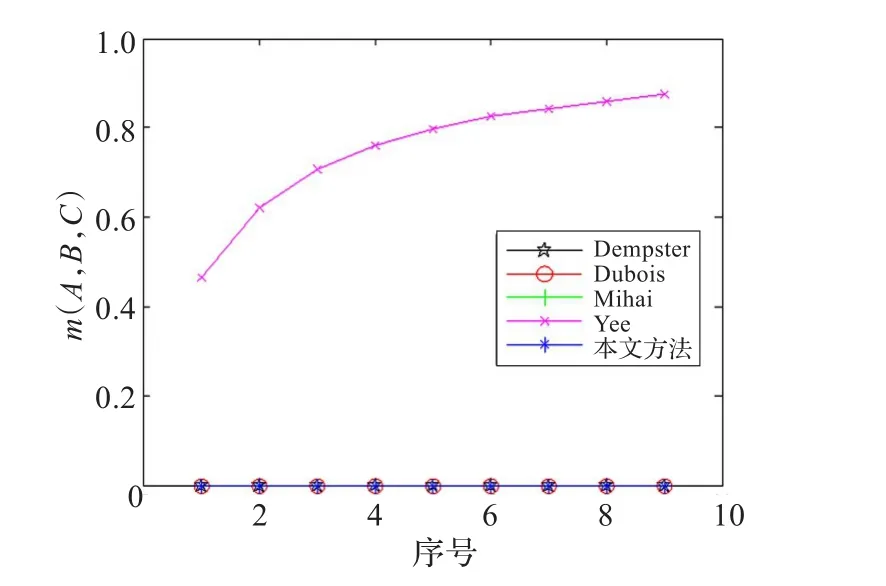
图8 m(A,B,C)变化曲线
5 结束语
本文研究了证据理论在高冲突环境下的多证据融合问题。通过对现有典型改进方法的分析,本文基于对现有两类证据理论改进方法的综合考虑,提出了一种基于交并集的冲突自适应证据组合方法。Matlab实验仿真结果表明,本文提出的方法能够有效解决证据理论的悖论问题。与典型改进方法相比,本文方法具有较高的收敛速度和区分能力,有效地解决了高冲突环境下的多证据融合问题。
冲突衡量是决定上述方法信任分配与合成效果的关键因素。因此,如何针对具体的应用环境,改进上述算法的冲突衡量方法是下一步工作的重点。
[1]Dempster A.Upper and lower probabilities induced by multivalued mapping[J].Annals of Mathematical Statistics,1967,38(2):325-339.
[2]胡昌华,司小胜,周志杰,等.新的证据冲突衡量标准下的D-S改进算法[J].电子学报,2009,37(7):1578-1583.
[3]陈金广,张芬.多证据源冲突的组合度量方法[J].计算机工程与应用,2013,49(9):222-227.
[4]Quost B,Masson M H,Denoeux T.Classifier fusion in the Dempster-Shafer frameworkusingoptimizedt-norm based combination rules[J].International JournalofApproximate Reasoning,2010,52(3):353-374.
[5]金宏斌,蓝江桥.超幂集下角度相似度的证据冲突判定方法[J].计算机工程与应用,2012,48(25):150-152.
[6]Su Zhigang,Wang Peihong.Maximal confidence intervals of the interval-valued belief structure and applications[J].Information Sciences,2011,181(9):1700-1721.
[7]Wang Ying-Ming,Yang Jian-Bo,Xu Dong-Ling,et al.On the combination and normalization of interval-valued belief structures[J].Information Sciences,2007,177(2007):1230-1247.
[8]Xu Xiaobin,Feng Haishan.An information fusion method of fault diagnosis based on interval basic probability assignment[J]. Chinese Journal of Electronics,2011,20(2):255-260.
[9]Zadeh L A.Review of Shafer’s mathematical theory of evidence[J].Artificial Intelligent Magazine,1984,5(3):81-83.
[10]Yager R R.On the fusion of imprecise uncertainty measures using belief structures[J].Information Sciences,2011,181(15):3199-3209.
[11]寻二辉,任趁妮.一种改进的冲突证据融合方法[J].计算机科学,2012,39(11):31-38.
[12]Leung Y,Ji Nannan,Ma Jianghong.An integrated information fusion approach based on the theory of evidence and group decision-making[J].Information Fusion,2012,23(2):1-13.
[13]Yager R R.On the Dempster-Shafer framework and new combination rules[J].Information System,1987,41(4):93-138.
[14]Dubois D,Prade H.Representation and combination of uncertainty with belief functions and possibility measures[J]. Computational Intelligence,1988,4(3):244-264.
[15]Florea M C,Jousselme A L,Bosse E,et al.Robust combination rules for evidence theory[J].Information Fusion,2009,10(2):183-197.
WANG Yongwei1,2,ZHAO Rongcai1,LIU Yunan1,2,SI Cheng1,2,QIU Wei1,2
1.Information Engineering University,Zhengzhou 450004,China
2.Henan Key Laboratory of Information Security,Zhengzhou 450004,China
According to the problem of Zadeh paradox in the high confliction environment,a confliction adaptive combination method based on intersection and union is proposed.The reliability of evidence is calculated based on the conflict matrix which is used to discount the evidences.The weight of intersection and union in the combination rule is dynamic adjusted based on the confliction of evidences.The trust of multi-element focus elements is redistributed to the single element focus elements.Experimental results show that the proposed method has fast fusion efficiency and good distinguishment which can effective dissolve the problem in the high confliction environment.
evidence theory;combination rule;conflict;information fusion
针对证据理论在高冲突环境下的Zadeh悖论问题,提出了一种基于交并集的冲突自适应多证据融合方法。基于冲突矩阵计算证据的可信度,并依据可信度对证据进行折扣;基于证据间的冲突关系对组合规则中交集命题与并集命题的权重进行动态调整;将多元素焦元的信任在单元素焦元中进行再分配。Matlab实验仿真结果表明,与典型改进方法相比,该方法具有较高的收敛速度和区分能力,有效地解决了高冲突环境下的多证据融合问题。
证据理论;组合规则;冲突;信息融合
A
TP393.08
10.3778/j.issn.1002-8331.1307-0154
WANG Yongwei,ZHAO Rongcai,LIU Yunan,et al.Confliction adaptive combination method based on intersection and union.Computer Engineering and Applications,2013,49(23):242-246.
国家高技术研究发展计划(863)(No.2012AA012704);国家重点基础研究发展计划(973)(No.2011CB311801)。
汪永伟(1977—),男,博士研究生,讲师,主要研究方向为网络与信息安全;赵荣彩,教授,博士生导师,主要研究方向为网络与信息安全;刘育楠,副教授;司成,硕士;邱卫,硕士。E-mail:wywyongweip@126.com
2013-07-12
2013-08-27
1002-8331(2013)23-0242-05

