望目特性连续型参数稳健设计遗传优化方法
沈 玲,曾 强,宋红娜,吴立云
1.河南理工大学 安全科学与工程学院,河南 焦作 454000
2.河南理工大学 能源科学与工程学院,河南 焦作 454000
望目特性连续型参数稳健设计遗传优化方法
沈 玲1,曾 强2,宋红娜2,吴立云2
1.河南理工大学 安全科学与工程学院,河南 焦作 454000
2.河南理工大学 能源科学与工程学院,河南 焦作 454000
参数稳健设计对于提高系统输出特性的稳定性具有重要意义。参数稳健设计的实质是通过合理确定系统输入参数的取值使系统输出特性达到理想值。系统输入参数按是否可控分为可控参数和不可控参数两种,其中,不可控参数是定值,设计者不能改变,可控参数则允许设计者进行优化决策以提高输出特性的质量。按可控参数是否连续可分为如下三类,全部参数连续(A类)、全部参数离散(B类)、部分参数连续部分参数离散(C类)。离散型参数具有有限个水平,连续型参数则相当于具有无穷多个水平。系统输出特性按性质可分为望目特性(a类)、望小特性(b类)和望大特性(c类)三类,其中,望目特性是指希望输出特性值y达到或接近目标值m而波动越小越好的质量特性[1]。若按输出特性值y的获取方式来划分可将系统参数稳健设计分为如下两类:通过试验方法获取(I类)、直接通过理论公式计算得到(II类)[2]。望目特性参数稳健设计是指通过合理确定可控参数的取值,使输出特性值y达到或接近目标值m且波动最小。望目特性连续型参数稳健设计是一个复杂的多目标组合优化问题,传统的数学方法无法对其求解,有必要研究并提出有效的求解方法。本文研究A-a-II问题(可通过理论公式计算得到输出特性值的望目特性连续型参数设计问题)的有效求解方法。
近年来,国内外学者对参数稳健设计进行了大量研究。日本统计学家田口玄一率先提出了一种基于“内表”、“外表”正交试验的田口方法[1-2]。田口方法可实现用尽可能少的试验找到满意解,在国内外工程实践中得到了广泛的应用[3-6]。然而,随着人类的不断进步,对A-a-II类问题田口方法逐渐暴露其不足。首先,田口方法计算量大、计算过程繁琐,短期内难以被工程人员掌握[7]。其次,田口方法对于望目特性参数设计试验方案采用信噪比η作为衡量指标本身存在缺陷,因为η是 μ2与σ2的比值,不能单从η的大小来衡量试验方案的优劣,比如 μ>>m,σ很小时η却很大,即由指标η得到的最优解无法控制输出特性的偏移量。文献[8]针对这一缺陷提出了改进措施,将η=μ2/σ2转换为从而既控制了输出特性的偏移量又控制了波动量。但改进后的η未考虑最优解对应的输出特性值y与目标值m的接近程度,需要进一步改进。再次,对可控参数进行离散化处理从而划分水平从理论上说有可能排除了最优解,得到的解仅属于局优解。对于第II类问题,由于其输出特性可直接通过理论公式计算得到,因此为改进解的质量,应当采用“密集抽样”取代“离散化处理”。密集抽样主要有两种措施,其一是大量增加可控参数水平数,其二是取消水平划分,代之以随机产生。前者属于近似密集抽样,随着水平数的增多和参数数目的增多,其内表试验次数大大增加,导致外表也大大增多,计算量巨增。后者才是真正意义上的密集抽样,但无疑也会大大增加计算量。近年来,部分学者提出采用遗传算法来解决参数稳健设计问题[7,9],其基本思路是增加可控参数水平数,然后采用遗传算法从各种组合中选优,究其本质仍是建立在对可控参数的离散化处理的基础上,属于近似密集抽样。对于多目标的处理方法主要有两种,一种是多目标单一化法,另一种是基于Pareto寻优的方法。前者通过某种转换过程(如加权平均)将多个目标转化为单一目标[10-11],然后采用单目标优化方法求解。相对于基于Pareto寻优的方法来说,前者较为简单,可直接获得最优解以供设计者决策,故本文选用多目标单一化法。遗传算法模拟生物进化原理,通过种群的选择、交叉、变异等措施实现逐步迭代优化,具有较强的鲁棒性、并行性和全局搜索性[12-13],对求解大规模组合优化问题具有优势,在工程实践中得到广泛的应用。本文研究的问题属于大规模组合优化问题,可考虑采用遗传算法求解。
基于以上分析,针对一类可通过理论计算得到输出值的望目特性连续型参数稳健设计问题(A-a-II问题),提出了一种基于遗传进化的望目特性连续型参数稳健设计方法:以密集抽样取代离散化处理,以个体取代试验方案,以变化的种群取代固定的内表,通过遗传进化得到最优设计方案。在此基础上,提出并设计了一种遗传进化算法对该类问题进行求解。最后,通过案例分析验证了本文所提方法的有效性。
1 变量定义
为便于本文的描述,定义了如表1所示的变量。
2 问题描述
若y是望目型输出特性值,其目标值为m,E和L是影响输出特性值y的因素取值,即 y=f(E,L),E为可控参数取值,其中各因素为连续型量,L为不可控参数取值。设y~N(μ,σ2)(因正交试验的参数组合具有均匀性、正交性特点,其输出特性值y在试验次数n较大时近似服从正态分布),其概率密度函数如图1所示。按文献[1]对稳健性的定义可得,稳健性参数设计的目标是合理确定E,使得式(1)、(2)在满足式(3)、(4)的约束条件下成立。

表1 变量定义

图1 y的概率密度图

式(1)保证了解E,L输出特性值y等于或接近目标值m(满足一般优化设计的任务),式(2)保证了解E,L中各分量波动时输出特性等于或接近目标值m(满足稳定性设计任务),即反映了解的“抗干扰”能力。式(2)中ΔE、ΔL是变值,导致该式不确定,故直接用其作为优化目标不现实,需从另外的角度进行转化处理。从统计学角度看,式(2)反映了解E,L输出特性值y的统计特性,可用|u-m|、σ2来综合衡量。如图1所示,|μ-m|反映了E,L对应输出特性值总体均值μ偏离目标值m的程度,σ2反映了E,L对应输出特性值总体波动程度,只有当二者均很小时,解E,L输出特性值y才具有很强的稳定性。基于以上分析,同时为便于后文用遗传算法求解,将式(1)、(2)转化为式(5)所示的单一优化目标。式(5)中,调节系数c1、c2、c3可根据三者之间的比例关系及设计者的期望(期望哪个小,则将其系数取大些,从而起到一种导向的作用)进行人工确定。

式(3)为可控参数范围约束,式(4)为技术约束,由系统设计结果确定。显然,这类优化问题是一复杂的组合优化问题,一般的数学方法无法对其求解,基于此,本文提出一种望目特性连续型参数稳健设计遗传优化方法。
3 望目特性连续型参数稳健设计遗传优化方法
基于遗传进化的望目特性连续参数稳健设计优化方法基本技术思路如下:
首先,对可控参数取值E进行改进。取消可控参数的水平划分(离散化处理过程),代之以密集抽样,即 E(j),j=1,2,…,v在B(j)~U(j)之间随机取值。
其次,采用如下的方法实现遗传优化。图2代表规模为ps的种群,相当于田口方法的内表,其中每一行代表一个个体,每个个体相当于一个试验方案,对应于一个“外表”。图2中,每个个体i,i=1,2,…,ps,是由v个可控参数取值 Ei(1),Ei(2),…,Ei(j),…,Ei(v)和w个不可控参数值L(1),L(2),…,L(w)组成。分别将 Ei(1),Ei(2),…,Ei(j),…,Ei(v),L(1),L(2),…,L(w)减去和加上对应的容差,各得3个水平:Ei(j)的1、2、3水平分别为Ei(j)-T1(j)、Ei(j)、Ei(j)+ T1(j),同理 L(j)的1、2、3水平分别为 L(j)-T2(j)、L(j)、L(j)+T2(j)。根据v+w个因素3个水平选用合适的正交表,即所谓的“外表”,由于输出特性值 yi,i=1,2,…,n可直接由理论公式计算得到,故容易用 excel求得yk,k=1,2,…,n及|yˉ-m|,Ve,y,|y-m|,根据式(5)可求得对应的,i=1,2,…,ps。模仿生物进化原理,让种群中的个体进行交叉、变异,重新计算,i=1,2,…,ps,每代进化结束将最优个体保留到子代种群,并用变量将最优个体记录下来,经过若干代进化后即得到最优个体,输出最优解,L。
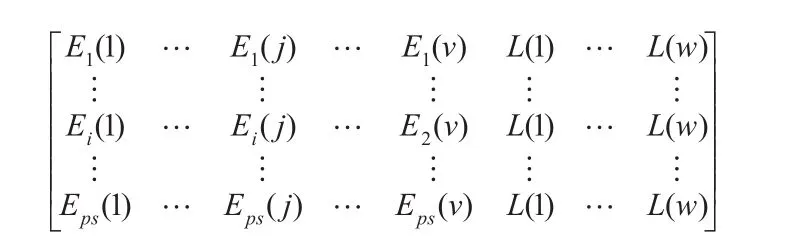
图2 种群示意图
最后,提出并设计相应的遗传算法对A-a-II问题进行求解。
4 望目特性连续型参数稳健设计遗传算法
根据A-a-II问题,提出并设计了相应的遗传算法(Genetic Algorithm,GA)。
4.1 算法流程
算法总体流程如图3所示。图中虚线框为保优策略,采用保优策略可使得最优个体始终保留在当前种群中。
4.2 适应度
由于式(5)是求最小化,而单目标遗传算法适用于求解最大化问题,为使适应度不至于过小或过大,再乘以一个正系数d,从而得到适应度f如式(6)所示。

4.3 个体编码
针对本文优化问题特点,仅对可控参数E进行编码,为此设计了如图4所示的实数编码方式,其编码长度为v,基因座1~v的基因值依次代表各可控参数的可行取值。
4.4 解码操作
解码操作的关键是确定正交试验表,一旦正交试验表确定,则可根据理论公式计算得到适应度。正交试验表取决于误差因素水平表和正交表。因是变量,L是定值,将v+w个因素分别减去和加上其对应的容差,将得到v+w个因素3个水平的误差因素水平表,如表2所示。根据误差因素水平表选定合适的正交表,如表3所示。正交试验表(表4)与正交表(表3)各单元格存在一一对应关系。对于正交试验表的某个单元格(如B3),根据正交表的对应单元格B2之值(水平号)采用excel的vlookup函数从误差因素水平表中查出该水平号对应的参数值,依次类推。例如,表4中单元格B3的取值通过式(7)所示的vlookup函数查询得到。然后,依次为正交试验表中单元格M3∶M(n+2),B1,N3∶N(n+2),D1,F1,H1写入相应的公式计算正交试验表的输出参数,其中单元格H1(1行,8列)为适应度对应的单元格。于是,通过VBA编写解码函数jm将个体的编码值存入单元格B4∶()4,()代表从B列往后第v列的列号,正交试验表自动更新且各输出参数自动计算,通过函数名jm返回单元格H1的值作为该个体的适应度。解码函数jm具体内容如下:

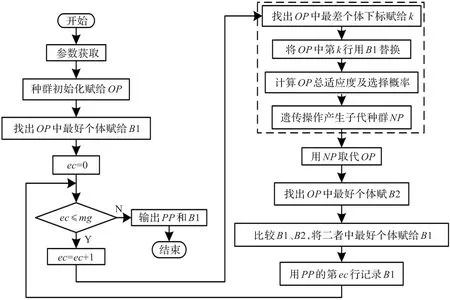
图3 算法流程图

表2 误差因素水平表(工作表)

图4 个体编码

表3 正交表(工作表)
4.5 种群初始化
种群初始化过程如下:对每个个体i(i=1,2,…,ps),根据可控参数 j(j=1,2,…,v),随机产生 B(j)~U(j)之间的实数,赋给E(j),通过解码操作计算其适应度f,将E赋给OP的末行前v列,将f赋给末行第v+1列。可见,采用这种方式产生的初始种群个体全部为可行个体。

表4 正交试验表(工作表)
4 .6 遗传操作
(1)遗传操作流程
遗传操作包括交叉操作和变异操作,本文设计的遗传操作流程如图5所示。
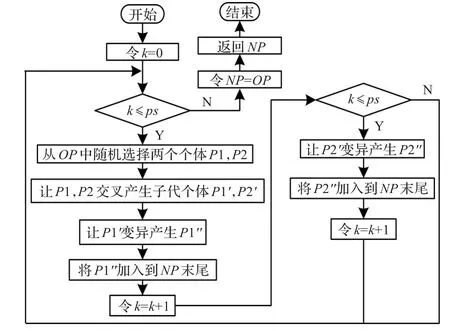
图5 遗传操作流程
(2)交叉操作
交叉操作目的是由两个父体P1和P2进行基因段的交叉,产生两个可行的子代个体。本算法采用两点之间对换的交叉方式,具体的交叉操作如下:
①随机产生0~1的实数r。
②若r≤pc则进行③~④,返回P1',P2',否则返回P1,P2,交叉操作结束。
③随机产生两个1~v的整数k1,k2并使k1≤k2。
④对换P1,P2的k1~k2之间的基因值得到P1',P2'。
(3)变异操作
变异操作目的是随机改变父体P某个或某些基因值,产生一个可行的子代个体。本算法采用了“一点”变异的变异方式,具体的变异操作如下:
①随机产生0~1的实数r。
②若r≤pm则进行③~⑥,返回P',否则直接返回P,变异操作结束。
③随机产生一个1~v的整数k代表要变异的基因位。
④随机产生一个B(k)~U(k)的实数s。
⑤令P(k)=s。
⑥对P重新解码得P'。
5 案例分析
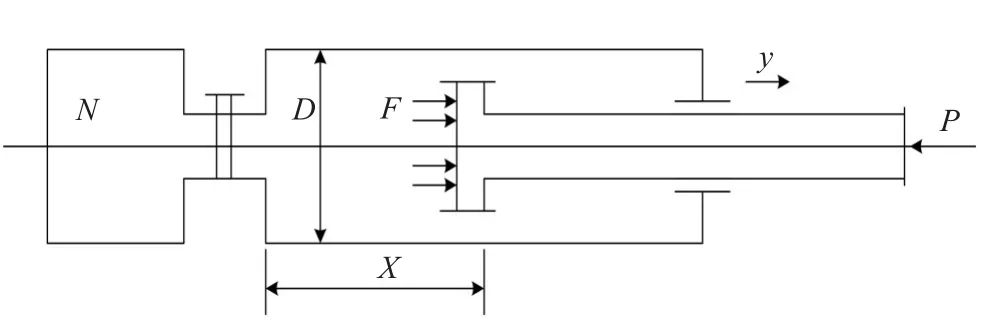
图6 某气动转向装置示意图

表5 正交表L18(21×37)
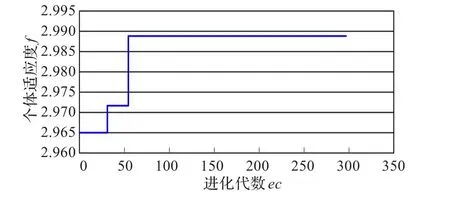
图7 进化过程图
以Excel 2007及其VBA为编程工具实现了上述算法,通过案例对本文所提方法进行有效性验证。某气动转向装置的系统结构如图6所示[1],可控参数依次为X、D、F,不可控参数依次为P、N,系统的输出特性值y为望目特性,其目标值m=960 mm/s,现要对该系统进行参数优化设计,使得输出特性值y稳定性最高。正交表[1],如表5所示,取n=18,采用本文提出的方法进行优化,得到的进化过程图如图7所示,最优解对应的正交试验结果如表6所示。文献[1]对应的最优解可见,本文得到的最优解从ˉ-m|、Ve、-m|三个指标看均明显优于文献[1]的最优解。再取c1=10.0,c2=1.0,c3= 10.0,其他条件不变,得到最优解E*=[ ] 52.35 25.72 0.3,对应的ˉ=959.53 mm/s,ˉ-m|=0.47 mm/s,Ve=3 360.91,y*= 960.17 mm/s,|y*-m|=0.17 mm/s,可见,由于增大了c1、c3使得最优解的ˉ-m|、|y*-m|明显减小,但Ve较c1=1.0,c2=1.0,c3=1.0的情况有所增大,但相较于文献[1]的最优解对应的Ve来说几乎相等,由此可见调节系数c1、c2、c3对最优解对应的ˉ-m|、Ve、|y*-m|有一定的导向作用。另外,经研究得知,不论c1、c2、c3如何变化,最优解对应的Ve均较大,这是因为容差T1、T2偏大的原因,为了进一步减小Ve以增强稳定性,可适当将容差减小。在此,假设将容差值缩小为原来的1/2,其他条件不变,得到的最优解可见,通过缩小容差,Ve明显减小,进一步增强了输出特性值y的稳定性,但是必须注意到,缩小容差毕竟会在一定程度上增加成本和加工难度,决策者应当在二者之间适当权衡。

式中,y为换向体速度,目标值m=960 mm/s;X为换向行程(mm);F为换向阻力(kgf);N为系统重量(kg);P为汽缸内气压(kgf/mm2);g为重力加速度(9 800 mm/s2)。

表6 E*对应的正交试验及解码结果
6 结论
本文针对一类可通过理论计算得到输出特性值的望目特性连续型参数稳健设计问题(A-a-II问题),提出了一种基于遗传进化的望目特性连续型参数稳健设计方法,基于该方法,提出并设计了一种遗传进化算法。通过本文的研究,得出以下主要结论:
(1)对可控参数的取值采用密集抽样,从理论上能找到比田口方法中离散化处理更好的解,案例分析也验证了这一结论。
(2)将田口方法中的信噪比η(η=μ2/σ2)用η′(η′=1/(c1× |μ-m|+c2×σ2+c3×|y-m|))更合理,后者能同时保证解E*,L输出特性值总体对目标值m的偏移程度小、波动程度小、y对目标值m的偏移程度小,从而能达到综合优化的目的。
(3)遗传算法中采用一种特殊的解码方式即借助正交试验表和excel公式自动计算得到适应度从而实现解码,免去了复杂的计算过程,使得计算效率高。
(4)本文方法便于为工程设计人员掌握,设计者只需根据可控参数和不可控参数个数选择合适的正交表,并通过excel对ˉ-m|、Ve、|y-m|、f及相关参数进行设置即可通过遗传算法快速找到最优解。
(5)本文方法适用范围具有可扩展性,不仅适用于望目特性,而且适用于望小特性和望大特性,但需要做适当修正才能适用。对于望小特性可令m=0,对于望大特性需将y进行倒数变换并令m=0。
[1]罗国勋.质量管理与可靠性[M].北京:高等教育出版社,2005.
[2]张公绪.新编质量管理学[M].北京:高等教育出版社,2003.
[3]刘久富,王宁生,丁宗红,等.三次设计的扩展介绍与探讨[J].工业工程,2002,5(1):50-54.
[4]李佳翔,韩之俊.基于田口方法的小批量生产过程控制[J].工业工程与管理,2009(1):31-35.
[5]Nakagawa T,Kirikoshi T.Robust parameter design methodology for microwave circuits considering the manufacturing variations[J].International Journal of Computer Science,2012,39(2):214-219.
[6]Antony J,Mazharsolook E,Kaye M.Application of Taguchi’s robust parameter design methodology for process improvement[J].Quality World,1996:35-41.
[7]Chatsirirungruang P.Application of genetic algorithm and Taguchi method in dynamic robust parameter design for unknown problems[J].InternationalJournalofAdvanced Manufacturing Technology,2010,47(9/12):993-1002.
[8]李泳鲜,李双义.气门弹簧三次设计中望目特性信噪比的存在问题与改进方法[J].内燃机学报,2001,19(3):279-282.
[9]李辉,赵立英,刘钦圣,等.应用遗传算法进行三次设计初探[J].北京交通大学学报,2006,30(6):106-110.
[10]曾强,杨育,王小磊,等.一类基于多个目标的制造任务优化分配方法[J].计算机工程与应用,2010,46(5):17-20.
[11]Nakagawa T,Kirikoshi T.Multi-objective robust parameter design methodology applied to microwavecircuit[J].Lecture Notes in Engineering and Computer Science,2012,2:973-978.
[12]张京钊,江涛.改进的自适应遗传算法[J].计算机工程与应用,2010,46(11):53-55.
[13]赵新超,韩宇,艾文宝.求解背包问题的一种改进遗传算法[J].计算机工程与应用,2011,47(24):34-36.
SHEN Ling1,ZENG Qiang2,SONG Hongna2,WU Liyun2
1.School of Safety Science and Engineering,Henan Polytechnic University,Jiaozuo,Henan 454000,China
2.School of Energy Science and Engineering,Henan Polytechnic University,Jiaozuo,Henan 454000,China
Aiming at the problem of robust continuous parameter design in the target being best,in which the output value can be got by theoretical calculation,an optimization method based on genetic evolution is proposed.The researched problem in this paper is described.The technical idea of the optimization method based on genetic evolution for the researched problem is presented.In the proposed method,the discretization is replaced by dense sampling,the experiment scheme is replaced by individual, the fixed internal table is replaced by transformable population,and the optimal design scheme is got through genetic evolution process.The genetic algorithm for robust continuous parameter design in the target being best is presented and designed.The calculation flow,the individual coding,the individual fitness,the population initialization,decoding operation and genetic operation are described.The effectiveness of the proposed method is validated by case study.
robust parameter design;target being best;continuous parameter;optimization method;genetic algorithm
针对一类可通过理论计算得到输出特性值的望目特性连续型参数稳健设计问题,提出了一种遗传进化方法。描述了研究的问题;提出了望目特性连续型参数稳健设计遗传进化方法的技术思路:以密集抽样取代离散化处理,以个体取代试验方案,以变化的种群取代固定的内表,通过遗传进化得到最优设计方案。提出并设计了一种望目特性连续型参数稳健设计遗传算法,阐述了算法的计算流程、个体编码、适应度、种群初始化、解码操作及遗传操作。通过案例分析验证了所提方法的有效性。
参数稳健设计;望目特性;连续型参数;优化方法;遗传算法
A
C93-03;TP391
10.3778/j.issn.1002-8331.1304-0394
SHEN Ling,ZENG Qiang,SONG Hongna,et al.Optimization method based on genetic evolution for robust continuous parameter design in target being best.Computer Engineering and Applications,2013,49(23):215-220.
国家自然科学基金(No.51104056);河南省教育厅科学技术研究项目(No.12B120005)。
沈玲(1980—),女,讲师,研究领域:可靠度工程、安全工程;曾强(1975—),男,博士,副教授,研究领域:工业工程;宋红娜(1978—),女,讲师,研究领域:工业工程;吴立云(1972—),女,副教授,研究领域:工业工程。E-mail:shenling@hpu.edu.cn
2013-04-26
2013-07-16
1002-8331(2013)23-0215-06
CNKI出版日期:2013-08-27 http://www.cnki.net/kcms/detail/11.2127.TP.20130827.1602.009.html

