基于集员滤波的选择权更新子带有源噪声控制

王海燕，刘庆华

桂林电子科技大学 信息与通信学院，广西 桂林 541004

基于集员滤波的选择权更新子带有源噪声控制

王海燕，刘庆华

桂林电子科技大学 信息与通信学院，广西 桂林 541004

1 引言

有源噪声控制（ANC）利用声波叠加原理[1]，通过次级声源产生一个与初级噪声幅度相同相位相反的声波，从而达到消减噪声的目的。Widrow等人[2]提出的滤波-XLMS算法（FXLMS）在有源噪声控制中用得最为广泛，它是考虑到误差通道的影响而对LMS算法的推广，这两种算法都是在均方误差准则下得到，因此算法收敛速度慢，对宽带噪声降噪效果差。为此人们根据宽带噪声频谱特性，提出了子带自适应滤波结构[3]。

传统的子带自适应滤波结构[4-5]是将全带自适应滤波器分割到各个子带上分别处理，每个子带单独使用一个自适应子滤波器，这种子带结构会在自适应滤波器的输出端产生混叠分量，从而使得传统子带自适应滤波器具有较高的稳态均方误差。为了解决传统子带自适应滤波器中存在的混叠分量问题，人们通过采用过采样滤波器组，具有频率间隙的滤波器组，或使用临界采样滤波器组，并在相邻子带之间增加交叉滤波器等方法来解决混叠分量问题，而Lee和Gan提出了一种新的子带自适应滤波器结构归一化子带自适应滤波（Normalized Subband Adaptive Filtering，NSAF）[6]则不再存在混叠分量问题。在NSAF结构中，通过在每个子带上使用相同的全带自适应滤波器，并使用一组约束条件来更新权系数，因而它具有较低的相关性和最小的扰动性，具有较好的收敛速度，在计算复杂度方面，由于采用了严格采样，与NLMS算法的计算量相当。然而在Lee和Gan的算法中采用的是定步长，同样在收敛速度和稳态均方误差之间存在折中问题，文献[7]中提出了一系列变步长算法在两者之间进行折中，但在计算复杂度方面都未明显降低；文献[8]则将集员归一化算法[9]（SM-NLMS）扩展到NSAF结构中提出SM-NSAF算法，不仅在收敛速度和稳态均方误差之间达到折中，而且降低了计算复杂度；文献[10]通过选择权更新的联合子带结构（SPU-CNSAF）来达到收敛速度、稳态均方误差、计算复杂度三者性能的改善；而文献[11]则提出了一种动态选择子带（DS-NSAF）方法，保证权系数更新始终沿着收敛的方向进行，从而降低计算复杂度。

本文针对宽带噪声有源控制，基于NSAF结构，建立了前馈ANC无延迟结构，将SM-NSAF算法扩展到滤波-XLMS算法中，并采用选择部分权系数更新来进一步降低计算复杂度。通过仿真实现了对宽带噪声的控制，验证了该结构算法的性能。

2 NSAF及SM-NSAF算法

2.1 NSAF算法

归一化子带自适应滤波器（NSAF）结构如图1所示，其中H0(z)，H1(z)，…，HN-1(z)是一组N带具有正交性的严格采样余弦调制滤波器组，ui(n)和di(n)为子带参考信号和期望信号，ui(n)通过自适应滤波器W(k，z)生成子带输出信号 yi(n)，对di(n)和 yi(n)进行N倍抽取生成子带抽取信号di，D(k)和 yi，D(k)，注意这里用n表示抽取前的因子，k表示抽取后的因子。

图1 NSAF结构

其中：

利用余弦调制滤波器组的正交性[12-13]，有如下对角化假设：

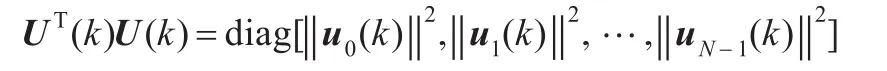
自适应滤波器系数向量更新公式可以写成：

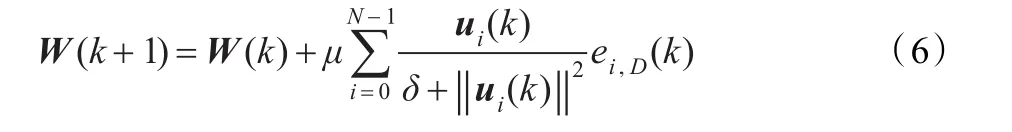
2.2 SM-NSAF算法

Gollamudi等[9]将集员理论推广到广义的滤波问题，建立了随机梯度算法的集员等价，即SM-NLMS算法。文献[8]将集员滤波的思想进一步推广到NSAF算法中，提出了具有数据选择性变步长更新的集员归一化子带自适应滤波（SM-NSAF）算法。

在SM-NSAF算法中定义输入-期望数据对的约束集为：

其中γ为噪声界，一般选用测量噪声v(n)。采用递推算法解上述定界椭球集合[9]，即在每个子带中将W(k)正交投影到最近的Ψk，i边界上，通过递推求得最优W(k+1)。

3 基于NSAF结构的前馈ANC算法

基于NSAF结构的前馈ANC算法结构如图2所示，x(n)为初级传感器拾取的参考信号，e(n)为误差传感器拾取的误差信号，P(z)为从初级传感器到误差传感器之间的传递函数，称之为初级通道；S(z)为从次级源到误差传感器之间的次级通道传递函数，称之为次级通道；Sˆ(z)是次级通道S(z)的估计，r(n)为x(n)经过Sˆ(z)后的滤波参考信号；实际应用中一般无法得知S(z)和d(n)，可以用其估计

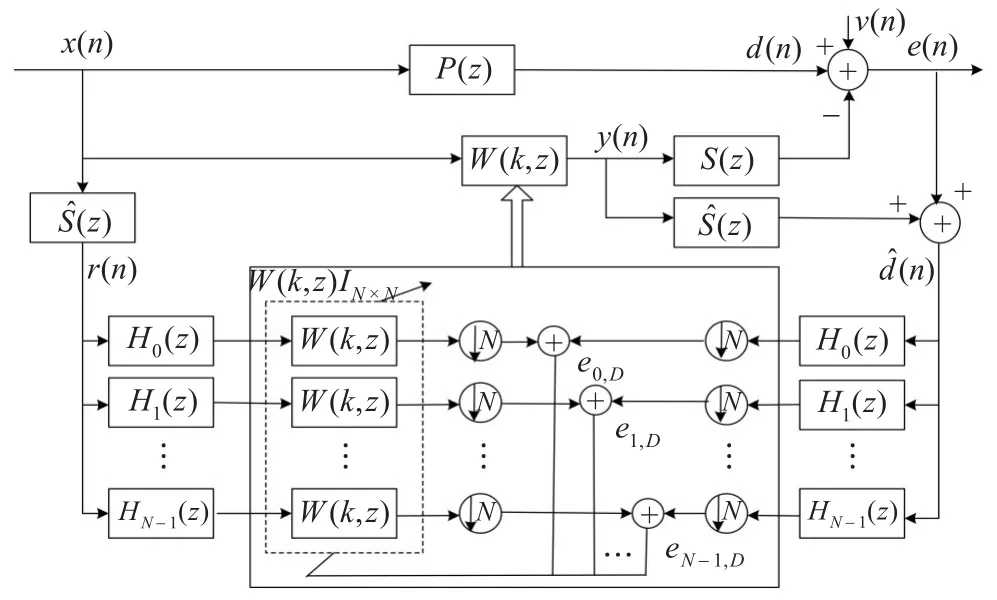
图2 基于NSAF前馈ANC结构

4 计算复杂度分析

根据文献[6]中，以每输入一个全频带信号需要的乘法次数为指标，NSAF算法需要的乘法次数为3M+3NL，与NLMS算法相比多3NL次，但由于在有源噪声控制中M>> NL，因此与NLMS算法计算复杂度相近。SM-NSAF算法权系数的更新由式（9）决定，小于NSAF算法，本文利用选择部分权进行更新，计算量进一步降低，小于S/B倍的NSAF算法。

5 仿真分析

下面通过对宽带噪声的仿真验证算法性能。设初级通道P(z)和次级通道S(z)长分别512阶和256阶；输入参考信号x(n)为零均值高斯白噪声通过带通滤波器生成的带宽为100～400 Hz带限高斯白噪声；系统噪声v(n)是均值为零、方差为σv2=0.000 1的高斯白噪声，且与输入信号相互独立；文献[14]讨论了γ值的选取，这里选取γ为σv；自适应滤波器长M=256，使用余弦调制滤波器组对输入信号和期望响应进行分割，比较N=8、N=16和B=16、B=64时的性能，所有仿真为100次独立实验平均后的结果。

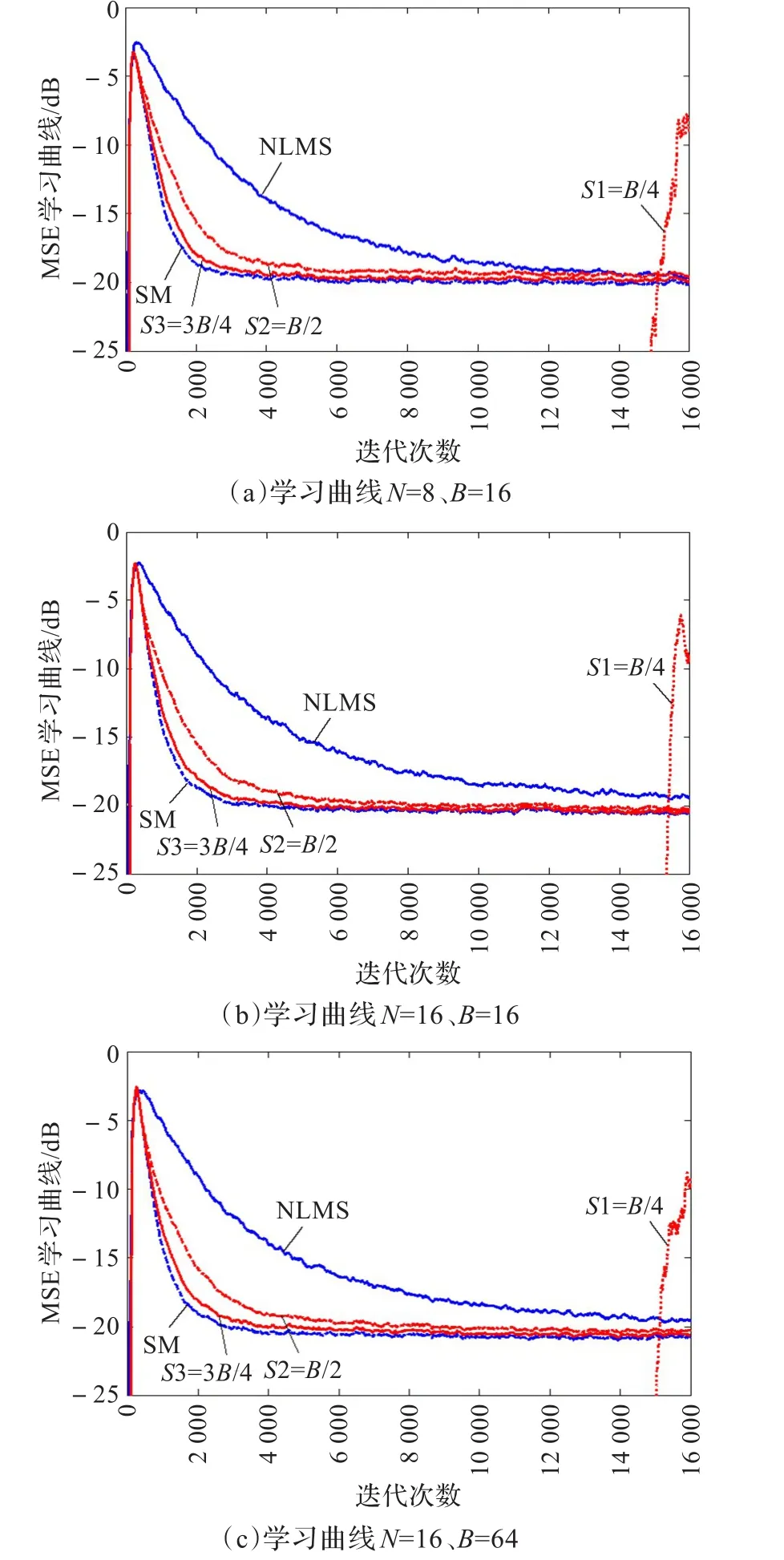
图3 N和B取不同值时MSE学习曲线

观察图3可见，子带NSAF算法优于全带NLMS算法。比较采用选择部分权更新时B=16和64的收敛曲线可以看出当S≥都可以有较好的收敛速度。对于收敛后的稳态均方误差，由于采用了集员滤波，它是一种变步长算法，所以可以获得较低的稳态均方误差。而N=16时收敛所需的迭代次数较少，可见分割子带数多时所需迭代次数较少。

图4给出了相应的功率谱密度，可以看出对于带宽为100～400 Hz带限高斯白噪声最终可以获得20 dB左右的降噪量。图5给出了N=16时，在条件的约束下每次迭代所需的子带数，这里对每个子带上的数据都进行了时间稀疏，每次迭代并不需要每个子带都进行更新，可以看到最多时只需5个，大大降低了计算量。

图6比较了本文算法与Morgan算法的性能，通过观察可以看出本文算法具有更快的收敛速度和更好的降噪效果。而且在本文算法中使用正交余弦调制滤波器组进行子带分解，产生实信号，更适合实际应用。

图4 N和B取不同值时误差信号功率谱密度

图5 N=16时每次迭代所需更新的子带数目

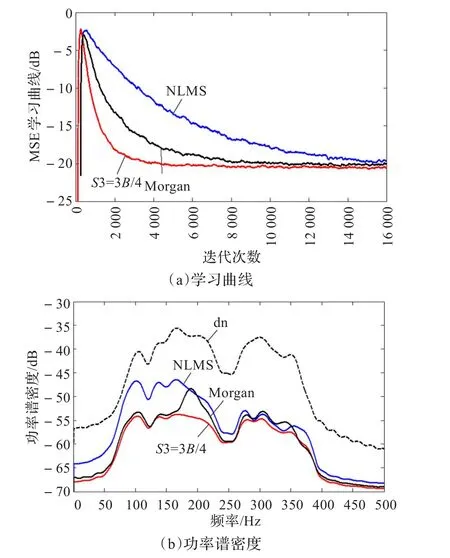
图6 与Morgan算法比较

6 结束语

本文建立了基于NSAF结构的前馈ANC算法结构，并基于集员滤波算法，结合利用选择部分权系数更新的方法减少计算量。仿真结果表明，当选择权系数更新块S≥时，都具有很好的收敛性能，同时由于采用集员滤波技术，对每个子带上的数据都进行了时间稀疏，大幅降低了计算量。本文算法与传统的无延迟子带算法相比具有更快的收敛速度和更好的降噪效果，而且通过使用正交余弦调制滤波器组进行子带分解，产生实信号，更适合实际应用。

[1]陈克安.有源噪声控制[M].北京：国防工业出版社，2003.

[2]Widrow B，Shur D，Shaffer S.On adaptive inverse control[C]// 15th Asilomar Conference on Circuits，Systems and Computers.Pacific Grove，CA：Acoustical Society of America，1981：185-189.

[3]Lee K A，Gan W S.Subband adaptive filtering：theory and implementation[M].Chichester，UK：Wiley，2009.

[4]Morgan D R，Thi J C.A delayless subband adaptive filter architecture[J].IEEE Trans on Signal Processing，1995，43（8）：1819-1830.

[5]Merched R，Diniz P S R，Petraglia M R.A new delayless subband adaptive filterstructure[J].IEEE Transon Signal Processing，1999，47（6）：1580-1591.

[6]Lee K A，Gan W S.Improving convergence of the NLMS algorithm using constrained subband updates[J].IEEE Signal Processing Letters，2004，11（9）：736-739.

[7]倪锦根.变设计参数子带自适应滤波器研究[D].上海：复旦大学，2010.

[8]Abadi M S E，HusØy J H.Set-membership subband adaptive filters[C]//Proc ISCCSP，2008，88（10）：2463-2471.

[9]Gollamudi S，Nagaraj S，Kapoor S，et al.Set-membership filtering and a set-membership normalized LMS algorithm with an adaptive step size[J].IEEE Signal Processing Letters，1998，5（5）：111-114.

[10]Liu Chang，He Miao，Xia Wei.Adaptive combination of subband adaptive filters with selective partial updates[C]// AICI，2011：204-211.

[11]Kim S E，Choi Y S，Song M K，et al.A subband adaptive filtering algorithm employing dynamic selection ofsubband filters[J].IEEE Signal Processing Letters，2010，17（3）：245-248.

[12]Lee K A，Gan W S.On the subband orthogonality of cosinemodulated filter banks[J].IEEE Trans on Circuits Syst II，2006，53（8）：677-681.

[13]Lee K A，Gan W S.Inherent decorrelating and least perturbation properties of the normalized subband adaptive filter[J]. IEEE Trans on Signal Process，2006，54（11）：4475-4480.

[14]Diniz P S R，Werner S.Set-membership binormalized datareusing LMS algorithms[J].IEEE Transactions on Signal Processing，2003，51（1）：124-134.

WANG Haiyan,LIU Qinghua

School of Information and Communication Engineering,Guilin University of Electronic Technology,Guilin,Guangxi 541004,China

Subband adaptive filter architecture is employed to improve wideband noise control effect.The Normalized Subband Adaptive Filter（NSAF）employs the same fullband adaptive filter in each subband,so that it can eliminate aliasing components in the output of the adaptive filter,having a good convergence performance and steady-state mean square error.However,because of using the fullband adaptive filter in each subband,the computational complexity is higher than conventional subband architecture.Set-Membership Filter（SMF）can effectively reduce the computation due to data-selective update.This paper establishes the ANC algorithm based on the NSAF,and combines with SMF and selective partial updates to reduce the computation.A better performance of the algorithm is demonstrated by simulation results.

normalized subband adaptive filter;set-membership filter;selective partial updates;active noise control

通过子带自适应滤波结构，可以提高宽带噪声降噪效果，归一化子带自适应滤波（NSAF）通过在每个子带上使用相同的全带自适应滤波器，消除了传统子带结构会在输出端产生混叠分量的问题，具有较好的收敛性能和稳态均方误差。但由于在每个子带上采用相同的全带自适应滤波器，计算量要高于传统子带结构，集员滤波（SMF）技术具有数据选择更新的特点，可有效降低计算复杂度。基于NSAF结构，建立了前馈ANC无延迟结构，并基于集员滤波技术，通过选择部分权更新来进一步减少计算量，仿真验证了该算法对宽带噪声具有更优的降噪效果。

归一化子带自适应滤波；集员滤波；选择权更新；有源噪声控制

A

TN911.7

10.3778/j.issn.1002-8331.1202-0395

WANG Haiyan,LIU Qinghua.Active noise control with selective partial updates subband architecture based on set-membership filtering.Computer Engineering and Applications,2013,49（23）：207-210.

广西自然科学基金（桂科自：0832007z）。

王海燕（1982—），女，研究生，主要研究方向为有源噪声控制。E-mail：whygirl2004@163.com

2012-02-21

2012-04-18

1002-8331（2013）23-0207-04

CNKI出版日期：2012-06-21 http://www.cnki.net/kcms/detail/11.2127.TP.20120621.1127.003.html