粗糙域Voronoi图离散生成算法研究

滑斌杰，林立忠，柴忠良

石家庄学院 计算机系，石家庄 050035

粗糙域Voronoi图离散生成算法研究

滑斌杰，林立忠，柴忠良

石家庄学院 计算机系，石家庄 050035

1 引言

Voronoi图是计算几何的一个重要分支，是一种关于空间临近关系的重要的数据结构，它在几何形体重构、计算机图形学、图形图像处理与模式识别、地学、物理、化学、生物学、地质、气象以及城市规划等领域有着广泛的应用，随着计算机技术的普及与发展，Voronoi图的应用领域也在不断扩大[1-2]。

在Voronoi图的研究方面，有两个主要方向，一是根据不同应用在母点（生成元）形状和生成面上的扩展，二是Voronoi图生成算法的研究。在母点和生成面的扩展方面有：线段Voronoi图、面Voronoi图、球面Voronoi图及其加权Voronoi图，流域Voronoi图、斜面Voronoi图和障碍Voronoi图等[2-6]。Voronoi图生成算法很多，总体上分为两类：矢量法和离散法。矢量法有对偶生成法、增量法、分治法、平面扫描法等。相对于离散生成法，矢量法生成Voronoi图算法和数据结构比较复杂，目前对Voronoi图生成算法的研究主要是离散法的研究。

Voronoi图离散生成算法的核心问题是生成面上两点间距离的计算。典型的距离有Euclid距离、Manhattan距离等，这些距离计算的前提是生成面上任意点对距离的影响权相等，即距离仅由两点的空间位置确定，而不考虑其他属性对距离的影响。在实际的应用中（例如地学、城市规划等），空间点所承载的信息量除了空间位置外，还有高程、人口密度、交通状况等因素，这些因素都会对Voronoi图的离散生成中距离的计算产生影响。

本文给出了粗糙域Voronoi图的定义并对其生成算法进行了研究，实现了粗糙域Voronoi图的离散生成，同时对粗糙域Voronoi图在母点加权、生成面障碍等方面的扩展提供了有价值的思路。

2 粗糙域Voronoi图

2.1 Voronoi图的数学定义

Voronoi图是根据已知点集（母点）对生成面的一种分割，其数学定义如下[2]：

定义1设 pi(i=1，2，…，n)为二维欧式空间（平面）上的n个互不相同的点。将由：

所给出的对平面的分割，称为以 pi(i=1，2，…，n)为母点（或生成元）的Voronoi图，简称V-图，其中d(p，pi)为点 p与 pi间的Euclid距离。

在V-图中，生成面被母点间的垂直平分线（段）分割成不相交的n各部分，如图1所示。生成面的分割线称为V-边，V-边的交点称为V-点，包含母点的不多于n-1条边的凸多边形区域称为母点的V-域。V-边是两母点间垂直平分线的一部分。

图1 Voronoi图

2.2 粗糙域的定义

一般V-图的生成面为普通二维欧式平面（D），平面上两点间的距离是两点空间位置的函数，即

而在实际的应用中（例如地学、城市规划等），空间点所承载的信息（空间点的某属性）是复杂的，这些信息可能对两点间距离的计算产生影响，这时，两点间的距离看成是包含两点空间位置在内的各种影响因素的函数，即

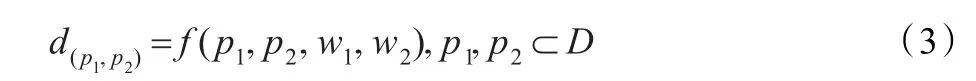
其中，w1、w2分别为 p1、p2两点对距离的影响权。由此给出粗糙域的定义。

定义2在某二维区域D内，若各点所承载的某属性值不同，称为区域D在此属性值上是粗糙的，把区域D称为基于此属性值的粗糙域。

图2是模拟的基于某属性值的粗糙域，粗糙域中各点的属性值由各点的灰度值表示。

2.3 粗糙域V-图的数学定义

生成面基于粗糙域的V-图称为粗糙域V-图。由于粗糙域中空间点对距离的影响权不同，所以在V-图的定义中以带权距离W(p，pi)来代替欧式距离d(p，pi)。W(p，pi)为基于某种搜索算法所获得的路径。根据V-图的一般定义，可知W(p，pi)为 p和 pi两点间的最优路径。粗糙域V-图数学定义如下：

定义3设 pi(i=1，2，…，n)为粗糙域上的n个互不相同的点。将由：

图2 模拟的基于某种属性值的粗糙域（粒度8×8）

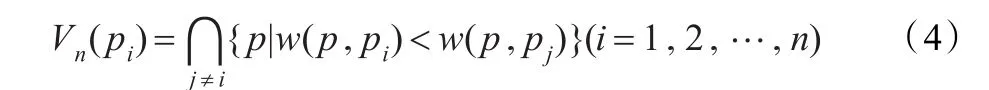
所给出的对粗糙域的分割，称为以 pi(i=1，2，…，n)为母点（生成元）的粗糙域V-图。在粗糙域V-图中，粗糙域被分割成不相交的n个部分，由于受粗糙域粗糙特性的影响，V-边为不规则曲线（段），如图3所示。

图3 粗糙域V-图

3 粗糙域Voronoi图的离散生成算法

3.1 基本思路

根据粗糙域V-图的数学定义可知，某母点的V-域是到本母点的最优路径长度比到其他母点的最优路径长度都短的点的集合。对于粗糙域上任意点p，如果能使用某种最优路径搜索算法，计算出点p到所有母点的最优路径，点p就属于最优路径最短的母点的V-域。所以粗糙域V-图的离散生成算法的关键是低复杂度且高效的最优路径搜索算法的选择。

A*算法是目前最流行的最优路径搜索算法[7]，在粗糙域Voronoi图的离散生成算法中，最优路径搜索算法选择A*算法。

3.2 A＊算法

A*算法[8-10]是在宽度优先搜索基础上的一种启发式有序搜索算法。所谓启发式搜索就是在状态空间中，对每一个搜索的位置进行评估，得到最好的位置，再从这个位置向下进行搜索直到目标。在启发式搜索中，对位置的评估用估价函数来表示。A*算法的算法思想可以表示为：假设有一个估价函数F，它是状态空间中节点状态的实值函数。在最优路径搜索过程中，并不是把所有可能的节点全部展开，而是利用这个特定的估价函数F对所有没有展开的节点逐个进行评估，从而找出最可能被展开的节点将其展开，直到找到目标节点为止。估价函数的定义如下：

其中，F(n)为起始节点到目标节点间通过节点n的最优路径的代价。g(n)为从起始节点到节点n的最优路径代价。h(n)为节点n到目标节点的代价估计。

在最优路径搜索过程中，为了增强估价函数的适应性和搜索效率，常常将估价函数乘以一权值W，即h*=h×W。权值W的确定没有明确的规则，往往根据经验或经过大量实验来确定。这样的不利结果是对W的精确度把握不够，不能在低复杂度条件下获得路径的最优结果，无法满足实时最优路径搜索的需求。而在粗糙域V-图的离散生成算法中，要进行多次最优路径搜索，所以快速、准确确定估价函数的最优权十分重要。

3.3 A＊算法估价函数最优权值的确定

基于粗糙域的最短路径与粗糙域的粗糙特性有关。在进行最优路径搜索时，估价函数权值的选取直接影响所得的结果路径是否最优和算法的效率。为了能够快速确定估价函数的最优权值，进行了以下实验：选取不同范围、不同粗糙程度、不同粗糙分布的区域，通过制定不同的估价函数、改变估价函数的权值计算最优路径，通过分析，确定最优权值与粗糙区域粗糙特性的关系。

3.3.1 算法步骤

（1）计算机模拟基于某种属性值的粗糙域，用灰度值表示属性值（如图2）。

（2）在粗糙域上确定起始点和终止点。

（3）确定估价函数。

（4）给定某权值W，进行最短路径搜索，记录搜索结果，并记录搜索的点数和路径的总长度。

（5）改变权值W，重复（4）。

（6）改变估价函数，重复（4）、（5）。

（7）改变粗糙域和起始点和终止点，重复（2）～（5）。

3.3.2 A＊算法估价函数权值与粗糙域粗糙特性的关系

通过实验，对A*算法估价函数权值与粗糙域粗糙特性的关系进行验证，以下是一组典型实验数据。

以8×8粒度、属性值波动范围在0～200产生随机粗糙域，估价函数采用Manhattan距离。实验中估价函数的权值取值1～50，进行50次最优路径搜索。图4是实验采取不同权值时A*算法最优路径所搜情况。图4（a）～（f）分别是估价函数权值为1、10、20、30、40、50时的最短路径。

表1是实验中估价函数取不同权值进行最优路径搜索的详细数据。W为估价函数所取的权值，L为最优路径的长度，SP为搜索的节点数。

图5为不同权值最优路径搜索的详细数据变化趋势。X轴表示权重，Y轴表示在一定权值下计算的路径长度和搜索点数。

图4 不同权值下最短路径情况

表1 不同权值最优路径搜索的详细数据

图5 不同权值最优路径搜索的详细数据变化趋势

根据实验结果，分析如下：

（1）从图5中看到，随着估价函数权值W增大，最短路径的长度先保持不变后逐渐增大，而搜索点数逐渐减小。同时图4也说明，随着权值W的增大，在状态空间的搜索范围逐渐减小，搜索范围在从起点到终点的方向上有逐渐增大的趋向性。这说明了：在实验中所选择的估价函数是有效的，并且最优路径跟估价函数的权值相关；选择合适的权值能够在结果路径保持最优的情况下，大大降低算法的搜索点数，从而减小算法的复杂度。

（2）在表1中，W=19是最短路径的长度逐渐增大的转折点，转折点对应的权值为估价函数的最优权，其值接近状态空间节点属性值绝对差的1/10。大量实验结果表明，A*算法估价函数最优权值与粗糙域粗糙特性正相关，最优权值均约为节点属性值绝对差的1/10。

（3）根据结论（2），在实时性要求较高的应用情境下，可以根据已获得的状态空间节点属性值的绝对差来确定估价函数的权值W。同时考虑不同应用对路径是否最优和算法复杂度的要求，在最优权值周围一小邻域内调整W的取值。

图6 一般V-图

图7 粗糙域V-图

图8 粗糙域Voronoi图小区域误差

3.4 粗糙域Voronoi图的离散生成算法描述

根据粗糙域V-图的数学定义和A*算法估价函数权值与粗糙域粗糙特性的关系，给出粗糙域V-图离散生成算法如下：

（1）在粗糙域上设置母点位置和相应V-域颜色。

（2）对粗糙域上的点p，根据选定的最优路径搜索算法，计算p到各母点的最优路径。

①计算p与母点作为矩形的角点，计算矩形范围内各点的灰度绝对差。

②根据矩形区域灰度绝对差确定A*算法估价函数权值。

③A*算法进行最优路径搜索。

④对所有母点重复①、②、③。

（3）比较 p点到各母点最优路径的大小，确定 p点属于最优路径最小的母点的V-域，并将 p设定为本母点V-域的颜色。

（4）重复（2）、（3），直到粗糙域上所有点计算完毕。

（5）根据所设定的各母点V-域不同的颜色值，抽取V-边和V-域。

4 实验结果及分析

在MS.NET 2005平台下开发程序，实现了粗糙域V-图的离散生成。系统硬件配置为：Inter®CoreTM2 Duo CPU P8600@2.4 GHz；2.0 GB RAM。

图6是不考虑其粗糙特性生成的一般V-图，图7是生成的粗糙域V-图，与一般V图相比，粗糙域V-图的V-边为任意曲线（段）且V-边的形状与母点的位置和粗糙域特性相关。

由A*算法估价函数最优权值与粗糙域粗糙特性的关系（2.3节），根据粗糙域特性获得估价函数的最优权值，使得A*算法的复杂度远小于O(n2)，对于母点个数为M的粗糙域V-图的离散生成，其算法复杂度则远小于O(n2×M)。

表2是不同母点个数，在不同大小、随机生成的粗糙生成面下，使用A*算法和优化A*算法生成粗糙域V-图的生成时间及优化率的比较。从结果数据可以看出，在粗糙域V-图离散生成的过程中，由于采用了优化算法，获得了A*算法估价函数的最优权值，使得进行每一次最优路径搜索的时间复杂度降低，最终导致粗糙域V-图离散生成算法复杂度明显降低。

表2 粗糙域V-图的生成时间及优化率比较

在粗糙域V-图离散生成过程中，根据3.3.2节中所述确定最优权值的方法，虽然算法的时间复杂度大大降低，但有时不能获得路径的最优解，这就有可能导致在V-边附近某些区域在V-域归属上的误判现象。如图8所示，图中中间方格部分被判定为属于V域①。

解决这种误判现象的方法是确定最优权值W时，令其减去一小常量ε(ε＞0)，这样算法的时间复杂度相对有所提高，但是能够保证得到最短路径的最优解，从而消除V-域的误判。

5 结论

本文提出了粗糙域V-图的概念，为了高效实现粗糙域V-图的离散生成，对粗糙域下A*算法估价函数最优权值进行了研究，给出了粗糙域V-图的离散生成算法并对算法进行了验证，算法的实现拓展了V-图在复杂生成面条件下的应用。例如，在商业选址中，人口密度分布，同行业竞争分布，交通状况等都是应考虑的因素，在选址过程中，可以根据各种因素构造粗糙域，并在此基础上进行商业选址分析。同时本算法没有考虑母点加权、生成面障碍等更为复杂的情况，需要在此方面做进一步的研究。

[1]刘金义，刘爽.Voronoi图应用综述[J].工程图学学报，2004（2）：125-132.

[2]张有会.加权Voronoi图画法的研究[J].计算机科学，2001，28（6）：126-130.

[3]张有会.线段加权的Voronoi图[J].计算机学报，1995，18（11）：822-829.

[4]Aichholzer O，Chen D Z.Skew Voronoi diagrams[J].International Journal of Computational Geometry and Application，1999，9（3）：235-246.

[5]NishidaT，SugiharaK.Stablemarker-particlemethod for the Voronoi diagram in a flow field[J].Journal of Computational and Applied Mathematics，2007，2（2）：377-391.

[6]赵仁亮.基于Voronoi图的GIS空间关系计算[M].北京：测绘出版社，2006：39-53.

[7]Nilsson N J.人工智能[M].郑扣根，译.北京：机械工业出版社，2000.

[8]杨素琼.基于A*算法的地图路径搜索的实现[J].铁路计算机应用，2000（4）：24-27.

[9]史辉.A*算法的改进及其在路径规划中的应用[J].测绘与空间地理信息，2009，32（6）：208-211.

[10]钟敏.A*算法估价函数的特性分析[J].武汉工程职业技术学院学报，2006，18（2）：31-33.

HUA Binjie,LIN Lizhong,CHAI Zhongliang

Department of Computer,Shijiazhuang University,Shijiazhuang 050035,China

Voronoi diagram is an important branch of computational geometry and Voronoi diagrams based rough area are extensions of Voronoi diagrams.In this paper,a conception of Voronoi diagram based rough area is proposed and it is generated with the minimum distance between points of forming face and mother-points which is calculated out using A-star algorithm.For reducing the complexity of generating algorithm,a research on relation between weight of evaluation function of A-star algorithm and character of rough area is launched.Experimental results show that the optimal weight of evaluation function positively correlates with the roughness characteristics of rough area.Based on this,the optimal weight of A-star algorithm is obtained and the complexity of generating algorithm of Voronoi diagrams based rough area is remarkably reduced.

Voronoi diagram;rough area;A-star algorithm;evaluation function;optimal weight

Voronoi图是计算几何的一个重要分支，粗糙域Voronoi图是Voronoi图概念在复杂生成面上的扩展。提出了粗糙域Voronoi图的概念并利用A*算法计算生成面上点与各母点的最短路径对其进行离散生成。为了降低粗糙域Voronoi图离散生成算法的复杂度，对粗糙域下A*算法估价函数权值与粗糙域粗糙特性的关系进行了深入探索。实验结果表明，A*算法估价函数权值与粗糙域粗糙特性正相关，并以此获得A*算法估价函数的最优权，大大降低了粗糙域Voronoi图离散生成算法的复杂度。

Voronoi图；粗糙域；A*算法；估价函数；最优权

A

TP391

10.3778/j.issn.1002-8331.1203-0245

HUA Binjie,LIN Lizhong,CHAI Zhongliang.Research on discrete generation algorithm of Voronoi diagram based rough area.Computer Engineering and Applications,2013,49（23）：191-194.

河北省科技型中小企业技术创新基金（No.11C1303111004）。

滑斌杰（1974—），男，工程师，主要研究方向：图形图像处理；林立忠（1964—），男，副教授，主要研究方向：软件工程；柴忠良（1961—），男，高级工程师，主要研究方向：人工智能、模式识别。E-mail：hbj.king.1974@163.com

2012-03-13

2012-06-25

1002-8331（2013）23-0191-04

◎信号处理◎