最小化TPE一元回归分类在人脸识别中的应用

王军琴

西安文理学院 物理与机械电子工程学院，西安 710065

最小化TPE一元回归分类在人脸识别中的应用

王军琴

西安文理学院 物理与机械电子工程学院，西安 710065

目前，已经存在许多人脸识别方法，如主成分分析（Principal Component Analysis，PCA）[1-2]、独立成分分析（Independent Component Analysis，ICA）[3]及线性判别分析（Linear Discriminant Analysis，LDA）[4-5]都可以成功地完成人脸识别，这些算法都通过估计低维子空间以达到降维的目的，实践证明，这样对人脸识别确实有效。此外，无监督特征提取融合监督分类的方法也被引入到分类中，即核PCA加LDA（KPCA+LDA）[6]。稀疏表示分类（Sparse Regression Classification，SRC）[7]也在人脸识别中得到了广泛的应用，并已成为计算机视觉领域的重要工具之一。

2010年，文献[8]将线性回归分类（Linear Regression Classification，LRC）算法引入到了人脸识别中，假设来自特定类的人脸图像一定位于某个线性子空间内，则类特定的投影矩阵可以在训练阶段用最小二乘法估计，可以用原始向量与投影向量之间最小距离准则来完成识别，实验结果表明，LRC的表现优于PCA、ICA、LDA等算法。为了进一步提高算法的性能，文献[9]提出了一种鲁棒线性回归分类（Robust Linear Regression Classification，RLRC）算法，通过借助于M-估计得到相应的回归参数，解决了光照变化大或具有噪声干扰的人脸识别问题。此外，为了克服线性回归中多重共线性的问题，岭回归和主成分回归方法得到了广泛的应用。文献[10]提出了改进的主成分回归分类（Improved Principal Component Regression Classification，IPCRC）算法，在应用主成分分析算法前先移除每幅图的平均项，丢掉前n个主成分，便于消除人脸识别中光照变化的影响，仿真结果表明，IPCRC算法在解决光照变化人脸识别问题时明显优于传统的主成分回归分类（Principal Component Regression Classification，PCRC）[11]、LRC、岭回归分类（Ridge Regression Classification，RRC）[12]和基于判别的人脸识别方法。

然而，现有的基于回归的方法，如LRC、PCRC、IPCRC、RLRC等都不能将分类中所有类的总类内投影误差计算在内，而且，为了克服光照变化问题，IPCRC剔除了前几个主成分，在光照变化的条件下确实可以提高分类性能，但同时也降低了在有表情和姿势变化条件下的性能，即现有的回归分类方法不能考虑到用于人脸识别的所有类的总类内投影误差[13]。

基于上述分析，提出了一种基于最小化总投影误差（Total Projection Error，TPE）的一元回归分类方法，通过最小化线性回归分类中所有类的总类内投影误差来提高人脸识别的鲁棒性，考虑总类内投影误差的目的是最小化类内重建误差，通过寻求一种更好的投影矩阵，使得所有类的总类内重建误差最小。因此，提出的方法可以估计投影矩阵，使线性回归分类中类间重建误差最小，实验结果表明了所提方法的有效性及鲁棒性。

1 线性回归分类

已知来自第i类的 pi张训练图像属于 N个对象，i=1，2，…，N，每张训练图像大小为a×b，用 vi，j∈ℜa×b，i=1，2，…，N，j=1，2，…，pi表示，而vi，j∈ℜa×b由一个列向量xi，j∈ℜq×1构成，其中q=ab。为了估计类的具体模型，将列向量xi，j组成一个类的类成员，因此，对于第i类，有：

式中，每个向量xi，j都是Xi的一个列向量，在训练阶段，用矩阵Xi表示类i，称为每个类的预测器。

对于任意属于第i类的数据向量x可以表示为第i类的训练图像的一个线性组合：

式中，βi∈ℜpi×1是回归参数向量，可用最小二乘法估计，估计的回归参数向量可写成：

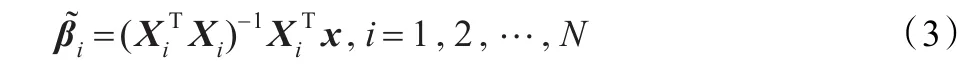
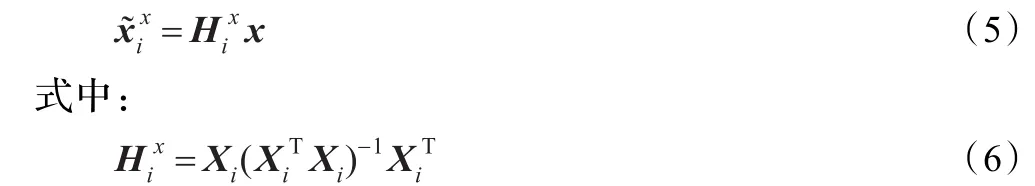
表示的是第i类的投影矩阵，该矩阵是一个对称矩阵也是等幂的。

LRC是基于每个类的测试向量与预测响应向量之间投影误差最小而开发的，所以在识别阶段，所有类投影矩阵，身份标识i*可以用最小投影误差来确定：

2 方法提出

给定所有类的训练图像集M，忽略它的类，每个训练图像大小为a×b，用vm∈ℜa×b，m=1，2，…，N表示，将每张图像都转换成一个列向量 xm∈ℜq×1，其中，q=a×b。组合所有的训练数据xm，数据的集合表示为X=[x1，x2，…，xm，…，xM]∈ℜq×M，为了确定它的类，用l(xm)∈{ } 1，2，…，C表示xm的类标签，其中，C是类的总个数。

2.1 最小化总投影误差的一元回归分类

所提一元回归分类（Unitary Regression Classification，URC）算法希望能够找到一个全局一元旋转矩阵U= [u1，u2，…，un，…，ud]，d≤q，它能将原始 X数据空间 xm旋转到一个低范围数据空间Z，以此来替代原始空间，有：

并在此空间内得到所有训练数据的最小总投影误差：

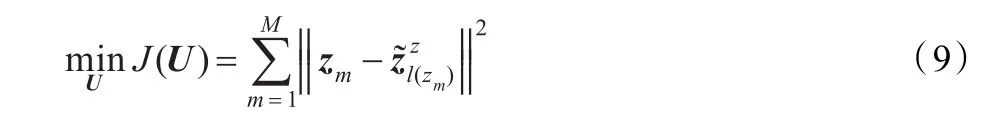
这表示l(xm)=l(zm)，提出的方法旨在为线性回归分类找到一元旋转矩阵U以实现总类间投影误差最小，由式（7）得，式（9）的目标函数可表示为：

将Zi=UTXi代入=Zi，可以很容易地得到=UTU，算术化简后，目标函数变为：

最后，目标函数可表示为：

利用拉格朗日乘数，求解下述特征分解问题可以得到投影矩阵的解：

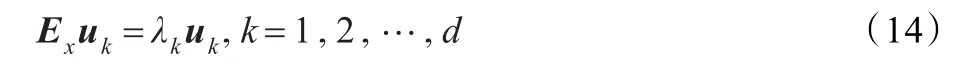
式中，λd≥…≥λk≥…≥λ1≥0

2.2 所提算法的统计学解释

为了减少模型的变异，岭回归（Ridge Regression，RR）方法提出添加一个惩罚因子到线性回归（Linear Regression，R）模型中，用以减少参数的变化，如＜，因此，岭回归能使回归模型稳定化，且执行效果优于线性回归。类似地，PCR和IPCR方法分别通过丢弃最后和开始的几个主成分方法减少回归模型的变化，有＜，＜。而提出的URC算法旨在使所有类的总投影误差最小，URC可以改变估计的总变化，使其最小化，因此，最小变化量的URC算法可以稳定地得到比其他回归分类算法更好的性能。

2.3 URC算法总结

提出的URC算法可以总结如下：

训练阶段：

步骤1给定一个人脸图像向量训练集，利用式（6）在原始向量空间找到类投影矩阵，利用式（12）计算所有训练数据的类内投影误差矩阵Ex。

步骤2求出特征分解问题的解Ex，利用式（14）找到一元旋转矩阵U。

步骤3利用zm=UTxm将每个训练图像向量转换为一个新的向量空间。

步骤4在旋转空间计算每个类的特定投影矩阵。

识别阶段：

步骤1利用z=UTx转换每个测试人脸图像向量x至旋转向量空间。

步骤2利用投影旋转向量z至第i类空间。

步骤3利用确定身份。

3 实验

所有实验均在4 GB内存Intel®CoreTM2.93 GHz Windows XP机器上完成，编程环境为MATLAB 7.0。

为了评估所提算法的性能，在两大公用人脸数据库：FEI[14]和FERET[15]上进行了测试，并且将提出的算法与本征脸[1]、Fisher脸[5]、KPCA+LDA[6]、SRC[7]、LRC[8]、RLRC[9]、PCRC[10]、IPCRC[10]等算法进行了比较。

3.1 FEI人脸库

FEI人脸数据库来自巴西圣保罗圣伯尔南多德坎普FEI人工智能实验室，该数据库包含200个对象（100个男性和100个女性），每个对象14张图像，共2 800张图像，如图1所示为FEI人脸数据库中某人的14张人脸图像示例。

图1 FEI人脸数据库中某人的14张人脸图像示例

在FEI人脸数据库中，最主要的挑战是数据库中的图像带有各种姿势变化，包括侧面像、面部表情变化（正常和微笑）、光照变化等，所有的图像都缩放成24×20大小。实验中，识别率由“留一法”（leaving-one-out）策略决定，表1、表2记录了各方法的实验结果，各方法的参数设置均参照各自所在文献，结果仅记录了最高识别率。

考虑了FEI数据库的在三种条件下是识别率，它们包括姿势变化（测试图像：1～10）、表情变化（测试图像：11、12）、光照变化（测试图像：13、14），从表1、表2可以看出，URC算法对侧脸轮廓的识别鲁棒性更好（测试图像：1、 10）；在有严重光照变化的条件下（测试图像：14）IPCRC的性能优于其他算法；在有表情变化的条件下，所提方法与各个比较的算法获得的结果相当。

表3显示URC得到的平均识别精度更高。从表3可以看出，所提URC算法在FEI人脸数据库上的平均识别率高于其他所有比较方法。

表1 各方法在FEI数据库上的识别率比较（测试图像为第1至第7张） （%）

表2 各方法在FEI数据库上的识别率比较（测试图像为第8至第14张） （%）

表3 各方法在FEI数据库上的平均识别率（%）

3.2 FERET人脸库

为了进一步评估提出的URC算法对姿势变化条件下的有效性，从FERET数据库中选择300个人的图像，每个人4幅图像，包括fa、fb、ql、qr，所有人脸图像均转换为灰度，剪裁并调整到24像素×20像素。如图2所示为FERET人脸数据库中某人的4张人脸图像示例，正面脸部图像fa和fb包含小姿势、尺度和表情变化，而ql和qr包含较大的姿势变化。

实验采用的是交叉验证方法，对每个识别实验，选取每个人的三幅图像用于训练，剩下的图像用于测试，各个比较方法的参数设置分别参照各自所在文献，进行了大量的实验，取各方法的最优识别率，实验结果如表4所示。

图2 FERET人脸数据库中某人的样本示例

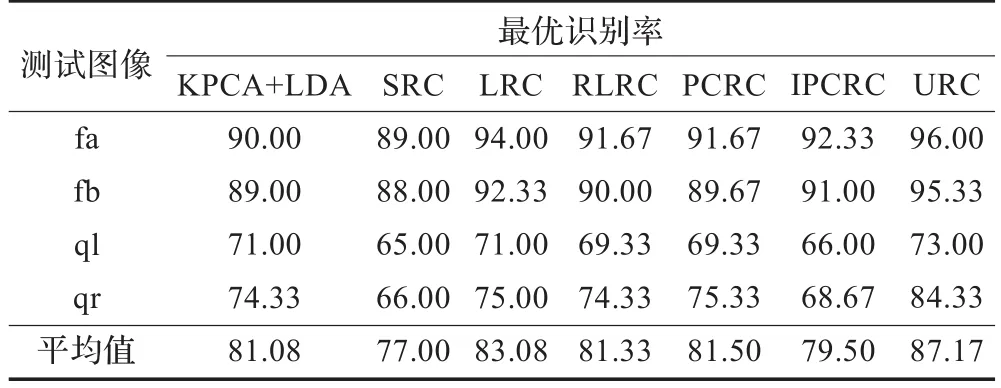
表4 不同方法在FERET数据库的性能比较 （%）

从表4可以看出，URC算法的执行效果优于其他各个算法，虽然SRC、RLRC和IPCRC算法能分别在噪声和光照变化条件下成功地识别人脸图像，但它们对姿势变化却是高度敏感的，所以，在处理具有较大姿势变化的人脸识别问题时，相比其他几种方法，所提方法的鲁棒性更加明显。

3.3 性能比较

为了更好地体现所提方法的优越性，将所提方法的计算复杂度与KPCA+LDA[6]、SRC[7]、LRC[8]、RLRC[9]、PCRC[10]、IPCRC[10]方法进行了对比，包括训练时间复杂度、测试时间复杂度及空间复杂度，具体比较结果如表5所示，其中，m、n分别表示图像矩阵的行数和列数，L、M、N分别表示投影向量数、测试样本数、训练样本数。

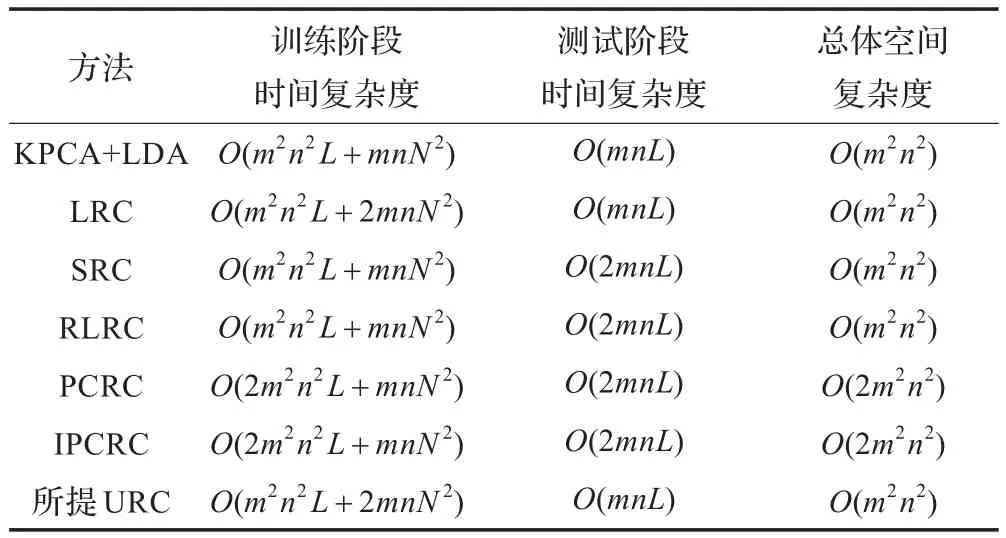
表5 各方法的复杂度比较

从表5可以看出，与KPCA+LDA方法相比，所提方法在训练阶段的时间复杂度稍微高了一点，其他均相同；与LRC方法相比，所提方法的各个复杂度均相当；与SRC、RLRC方法相比，所提方法在训练阶段的时间复杂度稍微高了一点，但是在测试阶段的复杂度却比SRC、RLRC低了很多，空间复杂度均相同；与PCRC、IPCRC方法相比，所提方法的训练阶段、测试阶段时间复杂度及总体空间复杂度均低了很多。综上可知，在大大地提高识别率的同时，所提URC方法仍然能够保持与其他各个比较方法相当甚至更优的时间、空间复杂度，由此可见其性能上的优越性。

4 结束语

针对现有回归分类方法不能很好地考虑用于人脸识别的所有类的总类内投影误差的问题，提出一种基于最小化总投影误差的一元回归分类方法，试图最小化所有类的总类内重建误差以找到线性回归分类的最优投影。实验结果表明，在处理具有姿势变化的人脸识别问题时，所提URC算法的识别性能明显优于本征脸、Fisher脸、KPCA+ LDA、SRC、LRC、PCRC、IPCRC和RLRC方法。

未来会结合其他技术，对回归分类方法的识别性能进行改进，通过设置不同的初始参数，进行大量的实验，从而找到最优参数，在提高识别率的同时，进一步改进算法的效率。

[1]徐明，乔宁博，文振焜，等.基于特征识别的三维人脸动画模型自动构造[J].中国图象图形学报，2012，17（12）：1540-1547.

[2]苏煜，山世光，陈熙霖，等.基于全局和局部特征集成的人脸识别[J].软件学报，2010，21（8）：1849-1862.

[3]柴智，刘正光.应用复小波和独立成分分析的人脸识别[J].计算机应用，2010，30（7）：1863-1866.

[4]邹建法，王国胤，龚勋.基于增强Gabor特征和直接分步线性判别分析的人脸识别[J].模式识别与人工智能，2010（4）：477-482.

[5]李晓莉，达飞鹏.基于排除算法的快速三维人脸识别方法[J].自动化学报，2010，36（1）：153-158.

[6]Yang J，Frangi A F，Yang J，et al.KPCA plus LDA：a complete kernel Fisher discriminant framework for feature extraction and recognition[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27（2）：230-244.

[7]宋相法，焦李成.基于稀疏表示及光谱信息的高光谱遥感图像分类[J].电子与信息学报，2012，34（2）：268-272.

[8]Naseem I，Togneri R，Bennamoun M.Linear regression for face recognition[J].IEEE Transactionson Pattern Analysis and Machine Intelligence，2010，32（11）：2106-2112.

[9]Naseem I，Togneri R，Bennamoun M.Robust regression for face recognition[J].Pattern Recognition，2012，45（1）：104-118.

[10]Huang S M，Yang J F.Improved principal component regression for face recognition under illumination variations[J]. IEEE Signal Processing Letters，2012，19（4）：179-182.

[11]李硕，汪善勤，张美琴.基于可见-近红外光谱比较主成分回归，偏最小二乘回归和反向传播神经网络对土壤氮的预测研究[J].光学学报，2012，32（8）：289-293.

[12]张曼，刘旭华，何雄奎，等.岭回归在近红外光谱定量分析及最优波长选择中的应用研究[J].光谱学与光谱分析，2011，30（5）.

[13]何林，潘静，庞彦伟.基于DCT和线性回归的人脸识别[J].计算机应用研究，2012，29（3）：1123-1126.

[14]周玲丽，赖剑煌.人脸特征的SIFT保护算法[J].中国图象图形学报，2011，16（5）.

[15]於东军，吴小俊，杨静宇.广义SOM及其在人脸性别识别中的应用[J].计算机学报，2011，34（9）：1719-1725.

WANG Junqin

School of Physics and Mechanical&Electronic Engineering,Xi’an University of Arts and Science,Xi’an 710065,China

For the issue that existing regression classification methods in face recognition do not consider total projection error within classes well,a unitary regression classification method based on minimizing Total Projection Error（TPE）is proposed. Characteristics decomposition is used to find unitary rotation matrix after the projection error matrix within class of all the training data is calculated by projection matrix of each class.Then,unitary rotation matrix is used to convert each training image vector to a new vector space,and the specific projection matrix of each class is worked out.Minimum projection error of each class in unitary rotating subspace is used to finish face recognition.The effectiveness and robustness of proposed method has been verified by experiments on the two common face databases FEI and FERET.Experimental results show that proposed method has better recognition accuracy than several other advanced regression classification approaches.

face recognition;minimizing total projection error;linear regression classification;unitary regression classification;unitary rotate subspace

针对人脸识别中现有回归分类方法不能很好地考虑总类内投影误差的问题，提出了一种基于最小化总投影误差（TPE）的一元回归分类方法。通过各个类投影矩阵计算所有训练数据的类内投影误差矩阵，并且借助特征分解找到一元旋转矩阵；利用一元旋转矩阵将每个训练图像向量转换为新的向量空间，并计算出每个类的特定投影矩阵；根据一元旋转子空间中各个类的最小投影误差来完成人脸的识别。在两大通用人脸数据库FEI和FERET上的实验验证了所提方法的有效性及鲁棒性，实验结果表明，相比其他几种先进的回归分类方法，所提方法取得了更好的识别效果。

人脸识别；最小化总投影误差；线性回归分类；一元回归分类；一元旋转子空间

A

TP391

10.3778/j.issn.1002-8331.1307-0346

WANG Junqin.Face recognition with unitary regression classification based on minimizing TPE.Computer Engineering and Applications,2013,49（23）：153-156.

王军琴（1978—），女，讲师，主要研究方向为人工智能、计算机控制。

2013-07-26

2013-09-10

1002-8331（2013）23-0153-04