基于差别矩阵的双射软决策系统的约简

吉晨莉，杨 勇

西北师范大学 数学与信息科学学院，兰州 730070

基于差别矩阵的双射软决策系统的约简

吉晨莉，杨 勇

西北师范大学 数学与信息科学学院，兰州 730070

1 引言

为了解决经济学、工程学、环境学及社会科学等各门学科中遇到的不确定的问题，一些数学理论和工具相继被提出，如概率论、模糊集、粗糙集等等。1999年，俄罗斯学者Molodtsov为更好地研究不确定现象，对现有的处理不确定性的工具进行了深入的分析，指出这些理论和结果都有其内在缺陷，比如可能性理论只可用于随机且稳定的问题，设定隶属度函数值是模糊集中存在的最大问题，而且这些方法都缺少参数化工具，由此提出了软集的概念[1]。目前，软集作为可以克服上述困难的唯一理论得到了广泛的应用。Maji P K等人[2]给出详细的软集理论后，在文献[3]中给出软集在决策中的应用，在文献[4-5]中给出了模糊软集的相关定义、结论和应用。Feng F等人在文献[6-7]中给出了软粗集、粗软集和模糊粗软集等的相关定义。基于软集理论，Gong K等人给出了双射软集和双射软决策系统的概念以及相关操作[8]。

属性约简是粗集研究的基本问题，同样也是软集理论中最为关键和棘手的问题。目前已有较多关于软集信息系统属性约简的方法[9-11]。在文献[8]中，Gong K等人利用依赖度不变的原则求双射软决策系统的约简，该方法比较复杂。本文将粗集理论中基于差别矩阵的属性约简方法[12]应用到双射软决策系统中，提出基于差别矩阵的双射软决策系统的约简方法，不仅简化了求约简的过程，又推广了粗集理论中的约简方法。

2 基本概念

2.1 软集基础

定义1（软集）设U是有限非空的对象集合，E是属性集合，P(U)表示U的幂集，A⊆E，设F:A→P(U)是一个A到P(U)的映射，则称(F，A)为U上的一个软集。

定义2（软子集）对于U上的两个软集 (F，A)和(G，B)，如果 B⊆A且 ∀b∈B，G(b)⊆F(b)，则称 (G，B)为(F，A)的软子集，记作(G，B)⊆～(F，A)。

定义3（软相等）对于U上的两个软集 (F，A)和(G，B)，如果(G，B)⊆～(F，A)且(G，B)⊇～(F，A)，则称这两个软集相等，记作(F，A)=(G，B)。

定义4（软集的交） U上的两个软集(F，A)和(G，B)的交集为(H，C)，其中C=A∩B，且∀e∈C，H(e)=F(e)∩G(e)，记作(F，A)(G，B)=(H，C)。

定义5（软集的并） U上的两个软集(F，A)和(G，B)的并集为(H，C)，其中C=A∪B，且∀e∈C

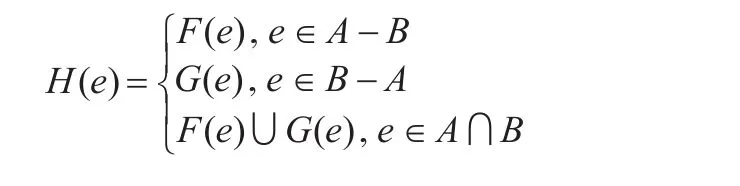
定义6（软集的与）U上的两个软集(F，A)和(G，B)，操作“(F，A)AND(G，B)”记作(F，A)∧(G，B)，且定义为(F，A)∧(G，B)=(H，A×B)，其中H(x，y)=F(x)∩G(y)，∀(x，y)∈A×B。

2.2 双射软集

定义7（双射软集）设(F，A)是U上的一个软集，其中F:A→P(U)是一个 A到P(U)的映射，A是非空属性集合。如果(F，A)满足以下两个条件：

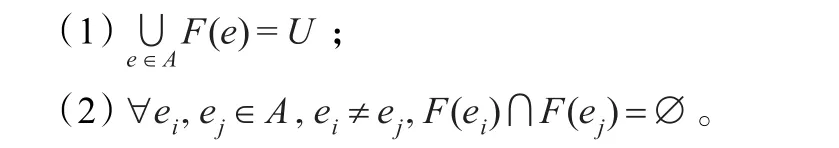
则称(F，A)为一个双射软集。

定理1如果(F，E)和(G，B)是U上的两个双射软集，则(H，C)=(F，E)∧(G，B)也是U上的双射软集。

3 基于差别矩阵的双射软决策系统的约简

类似于粗集决策表，双射软决策系统分条件软集和决策软集。在文献[8]中，Gong K等人利用依赖度不变的原则删除多余的条件软集，从而获得双射软决策系统的一个约简。本文基于差别矩阵，得到双射软决策系统的一种更简单迅速的约简方法，且能得到该系统的所有约简。

3.1 差别矩阵与差别函数

定义14（软集划分类）如果(F，A)是U上的一个双射软集，则(F，A)形成一个对U的划分，称(F，A)中的每个元素集合为软集划分类。

由定义7可知，在双射软决策系统中，条件软集形成条件划分类，决策软集形成决策划分类。

定义15（差别矩阵）设BSDS=((F，E)，(G，B)，U)是一个双射软决策系统，其中(Fi，Ei)是双射软集，则定义矩阵：

为双射软决策系统BSDS的差别矩阵，其中p，q=1，2，…，m，

根据对称性，Mm×m(BSDS)可表示成下三角矩阵或上三角矩阵，即

3.2 约简算法

输入 双射软决策系统BSDS=((F，E)，(G，B)，U)

输出 条件软集(F，E)相对于决策软集(G，B)的所有相对约简RED(G，B)((F，E))

步骤1计算双射软决策系统 BSDS的差别矩阵Mm×m(BSDS)。

步骤2对于差别矩阵 Mm×m(BSDS)中所有取值为非空集合的元素cpq(cpq≠∅∧cpq≠-)，建立相应的析取逻辑表达式Lpq如下：

步骤3对所有析取逻辑表达式Lpq进行合取运算，得到一个合取范式L∧(∨)(BSDS)如下：

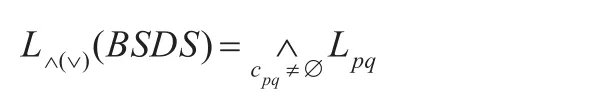
步骤4将合取范式 L∧(∨)(BSDS)转换为析取范式形式，得L∨(∧)(BSDS)=∨kLk。

步骤5输出

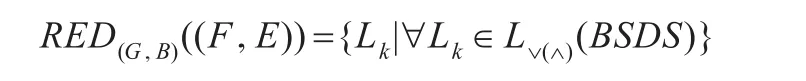
算法结束。

注 析取范式中的每个合取项Lk对应双射软决策系统的一个相对约简。

4 实例

设U={x1，x2，…，x6}是6个商店的集合，(F，E)和(G，B)分别是U上的条件双射软集和决策双射软集，其中E= E1∪E2∪E3，E1描述销售人员，取值为{high，med.，low}，E2描述商品质量，取值为{good，avg.}，E3描述交通阻塞情况，取值为{no，yes}，B描述盈利情况，取值为{profit，loss}。((F，E)，(G，B)，U)构成U上的双射软决策系统，其中(F，E)=且每个双射软集的映射定义如下：

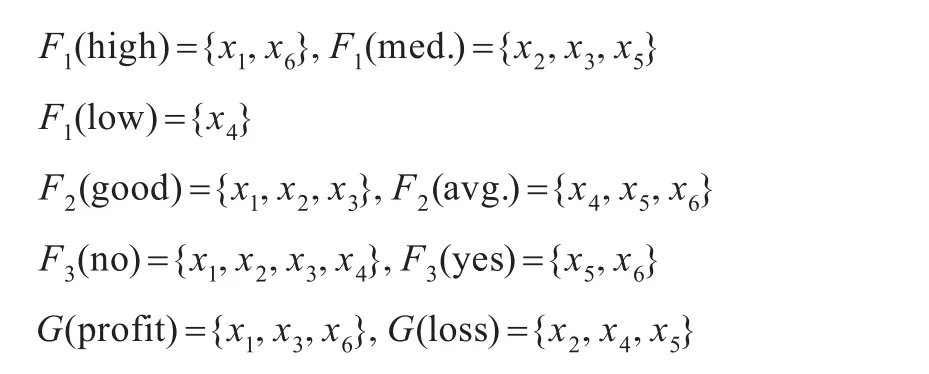
首先需要求出双射软决策系统的差别矩阵M6×6。根据定义 14，先取x2∈U，对于决策软集 (G，B)，x1∈G(profit)={x1，x3，x6}，而 x2∈G(loss)={x2，x4，x5}，故 x1，x2属于不同的决策划分类。对于条件软集(F1，E1)，x1∈F1(high)= {x1，x6}，而 x2∈F1(med.)={x2，x3，x5}，x1，x2属于不同的条件划分类，故(F1，E1)可以用来区分x1和x2，但(F2，E2)和(F3，E3)都不能用来区分 x1和 x2。所以c21=c12={(F1，E1)}。同理可以求出其余矩阵元素。为方便起见，将双射软集(Fi，Ei)简写为Fi，再根据对称性，最终得到一个下三角矩阵如下：

由差别矩阵可以求出差别函数Δ如下：

5 结语

在决策分析的应用中，类似于粗集属性约简，软集的约简也是一个重要的研究内容。选择一个好的约简方法有利于提高决策规则的提取效率。Gong K等人在文献[8]中利用依赖度不变的原则实现软集的约简，计算量比较大，而本文提出的基于差别矩阵的约简算法相对比较简单，且能到双射软决策系统的所有约简。在今后的工作中，将进一步研究双射软决策系统的约简方法。

[1]Molodtsov D.Soft set theory-first results[J].Computers and Mathematics with Applications，1999，37：19-31.

[2]Maji P K，Biswas R，Roy A R.Soft set theory[J].Computers and Mathematics with Applications，2003，45：555-562.

[3]Maji P K，Roy A R.An application of Soft sets in a decision making problem[J].Computersand Mathematicswith Applications，2002，44：1077-1083.

[4]Maji P K，Biswas R，Roy A R.Fuzzy soft sets[J].The Journal of Fuzzy Mathematics，2001，9（3）：589-602.

[5]Roy A R，Maji P K.A fuzzy soft set theoretic approach to decision making problems[J].The Journal of Fuzzy Mathematics，2007，203（3）：412-418.

[6]Feng F，Jun Y B，Zhao X Z.Soft semirings[J].Computers and Mathematics with Applications，2008，56（10）：2621-2628.

[7]Feng F，Li C X，Davvaz B，et al.Soft sets combined with fuzzy sets and rough sets：a tentative approach[J].Soft Computing，2010，14（9）：899-911.

[8]Gong K，Xiao Z，Zhang X.The bijective soft set with its operations[J].Computers and Mathematics with Applications，2010，60：2270-2278.

[9]Chen D G，Tsang E C C，Yeung D S，et al.The parametrization reduction of soft sets and its applications[J].Computers and Mathematics with Applications，2005，49：757-763.

[10]Kong Z，Cao L Q，Wang L F，et al.The normal parameter reduction algorithm[J].Computers and Mathematics with Applications，2008，56（12）：3029-3037.

[11]Ma X Q，Sulaiman N，Qin H W，et al.A new efficient normal parameter reduction algorithm of soft sets[J].Computers and Mathematics with Applications，2011，62：588-598.

[12]苗夺谦，李道国.粗糙集理论、算法与应用[M].北京：清华大学出版社，2008：186-192.

JI Chenli,YANG Yong

College of Mathematics and Information Science,Northwest Normal University,Lanzhou 730070,China

Based on the notions of bijective soft set and bijective soft decision system proposed by Gong K and so on,this article puts forward the method based on discernibility matrix to find the reductions of bijective soft decision systems.Using some natures of the discernibility matrix,this paper applies the method of finding reductions in rough set theory to the bijective soft decision system,which not only simplifies the process of finding reductions,but also generalizes the method in rough set theory. Key words：bijective soft set;bijective soft decision system;discernibility matrix;reduction

在Gong K等人给出双射软集和双射软决策系统概念的基础上，提出基于差别矩阵的求双射软决策系统约简的方法。利用差别矩阵的一些性质，把粗糙集理论中的约简方法应用到双射软决策系统中，既简化了求约简的过程，又推广了粗糙集理论中的约简方法。

双射软集；双射软决策系统；差别矩阵；约简

A

TP18

10.3778/j.issn.1002-8331.1202-0534

JI Chenli,YANG Yong.Reduction of bijective soft decision system based on discernibility matrix.Computer Engineering and Applications,2013,49（23）：103-105.

国家自然科学基金地区科学基金资助项目（No.61163036）。

吉晨莉（1988—），女，硕士研究生，主要研究领域为数据挖掘与粗糙集理论；杨勇（1967—），男，博士，教授，主要研究领域为粗糙集理论及其应用。E-mail：jcl_1128@163.com

2012-02-27

2012-05-08

1002-8331（2013）23-0103-03

CNKI出版日期：2012-06-21 http://www.cnki.net/kcms/detail/11.2127.TP.20120621.1127.001.html