基于MPSO-DV-Hop的无线传感器节点定位

周天绮，姜凤茹

1.浙江长征职业技术学院 计算机与信息技术系，杭州 310023 2.河南牧业经济学院 应用电子系，郑州 450044

基于MPSO-DV-Hop的无线传感器节点定位

周天绮1，姜凤茹2

1.浙江长征职业技术学院 计算机与信息技术系，杭州 310023 2.河南牧业经济学院 应用电子系，郑州 450044

当前无线传感器网络中的节点定位技术研究具有重要的理论和实际意义[1]，针对无线传感器网络节点定位问题，国内外学者进行了大量研究，主要有基于测距和免测距两类传感器节点定位算法[2]。测距算法需要利用距离或者角度信息进行节点定位，主要有RSSI、TOA、TDOA、AOA等定位算法，它们定位精度高，但功耗大、成本高，不适合用于低功耗、低成本的应用领域[3-5]。免测距算法根据网络的连通性来实现节点的定位，主要有质心算法、DV-Hop算法等，它们借助硬件设备少，计算简单，但定位精度低[6-8]。DV-Hop算法是一种应用最广泛的免测距算法，针对其定位精度较低的问题，许多学者对其进行了改进，如引入了全网平均跳距以减少每跳距离与实际距离间的误差；采用遗传算法、模拟退火算法、蛙跳算法、粒子群算法对DV-Hop算法的误差进行校正，一定程度上提高了DV-Hop算法的定位精度[9-11]。在这些算法中，粒子群算法具有参数少、搜索能力强等优点，与DV-Hop算法广泛应用于传感器节点定位。但在实际应用中，PSO算法存在一些不足，如在迭代后期，种群多样性降低，易陷入局部最优[12]。为了解决DV-hop算法定位精度低的难题，本文提出了一种多子群粒子群算法（Multi-subpopulation Particle Swarm Optimization algorithm，MPSO）优化DV-Hop的无线传感器节点定位（MPSO-DV-Hop）。实验结果表明，MPSO-DV-Hop提高了传感器节点定位精度，定位误差小，拓宽了WSN应用的范围。

1 DV-Hop定位算法

根据距离矢量和GPS定位原理，2001年，Nieuleseu等人提出了DV-Hop传感器节点定位算法，其只包含少数信标节点，剩余节点为未知节点，需要通过定位算法来确定它们的位置，具有无需测量距离，硬件要求低等点，在硬件条件有限的WSN得到了广泛的应用。DV-Hop算法的定位过程分为三个阶段：

（1）计算节点的最小跳数。信标节点向网络发送一个广播信号，邻居节点接收到信号后，记录信标节点的坐标信息，并保存每个信标节点的最小跳数，然后向其他的邻居传感器节点传播，通过该方法，WSN网络中全部节点可以得到信标节点的位置信息和与信标节点间的跳数。

（2）估算到信标节点的跳段距离。通过第一阶段后，每个信标节点就可以得到其他信标节点的坐标值和跳数，然后通过式（1）计算平均每跳距离，同时将每跳平均距离广播至网络中，未知节点只保存第一个每跳平均距离，并转发给邻居节点，未知节点将平均每跳距离值与最小跳数值相乘，得到其与信标节点间的距离[13-14]。

式中，h(i，j)是信标节点i和 j之间的跳数，(xi，yi)、(xj，yj)是信标节点i，j的坐标。

（3）通过最大似然法计算自身位置。设 P1(x1，y1)，P2(x2，y2)，…，Pn(xn，yn)表示n个信标节点的坐标位置，待定位节点 D的位置为(x，y)，其与标节点估计距离分别为d1，d2，…，dn-1，可以建立式（2）的方程：

在测距过程，由于多种因素影响会产生一些随机误差，最合理的线性方程组应为 AL+N=b，N为n-1维随机误差向量，采用最小二乘法得到方程组的解为：

2 MSPO-DV-Hop的节点定位算法

2.1 节点间跳数引起的误差及改进

DV-Hop算法的最大误差如图1所示。在图1中，节点B、C获得与信标节点A间的跳距，信标节点计算网络平均每跳距离且在网络中传播，未知节点B、C接收到距离最近的信标节点A的平均每跳距离并乘以跳数得到AB和AC跳段距离（如图1虚线所示），但是AB和AC的实际距离应为L1和L2，因此当最小跳数过大，易产生定位误差，且跳数过大误差越大。为了减少这一误差，对最小跳数进行判定，假定M为某一门限值，若h＞M，则h=M；若h＜M，则保持跳数不变。

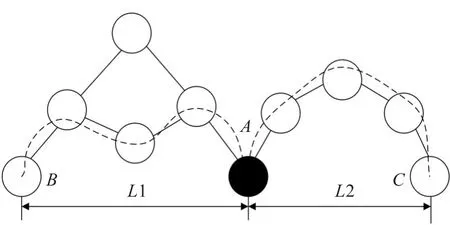
图1 DV-Hop节点分布图

2.2 最小二乘法引起的误差及修正

2.2.1 误差分析

从式（4）可知，dn是带有误差的测量距离，而向量b每个元素均包含dn，当dn的误差相当小时，那么最小二乘得到节点定位结果可以满足实际要求，但当dn的误差较大时，即使d1，d2，…，dn-1的误差小，节点定位的误差也将很大。

设信标节点(xi，yi)，i=1，2，…，n，与未知节点(x，y)的实际距离为 ri，i=1，2，…，n，测距误差 εi，那么|ri-di|＜εi，i=1，2，…，n。根据式（2）可知，(x，y)应该满足如下约束条件：

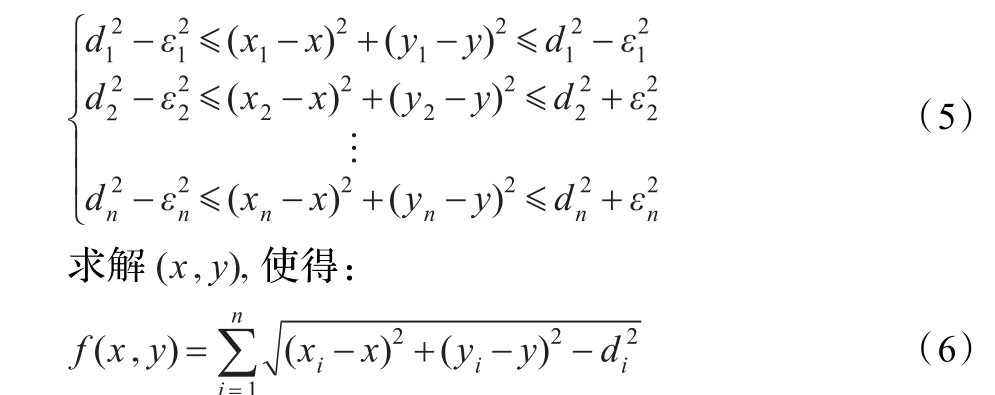
由于式（5）代表可行解的区域，那么该区域一定存在最优解，且当 f(x，y)最小值时，节点定位总误差最小，此时的坐标(x，y)将为最优值，这样无线网络传感器节点定位问题转化成一个约束优化问题，因此采用MPSO对式（6）进行求解。

2.2.2 MPSO算法

设粒子群在d维的空间搜索，粒子i的速度和位置分别为：vi=(vi1，xi2，…，vid)T和 xi=(xi1，xi2，…，xid)T，粒子i自身的历史最优位置为 pi=(pi1，pi2，…，pid)，种群历史的最优位置为 pg=(pg1，pg2，…，pgd)，其速度和位置更新方式为：

其中，c1、c2为加速系数；rand()为[0，1]之间的随机数；t为当前迭代次数；w为惯性权值。

在PSO算法中，当某粒子发现一个局部最优点时，其他粒子迅速向它靠拢，则粒子群就陷入局部极值点。为了解决该难题，将粒子群分为“利用”和“探索”两类子群，“利用子群”对探索到的最优区域进行精细搜索，“探索子集”探索有希望的区域，从而保持子种群的多样性。在图2中，Sbi为具有N个粒子的子种群，Sbi_1为利用子群，Sbi_2为探索子群，在每次迭代过程中，依据粒子适应度值，将Sbi分为Sbi_1和Sbi_2两个子群，它们粒子个数根据式（9）、（10）确定，两个子集群按照各自规则操作后，重新归队。

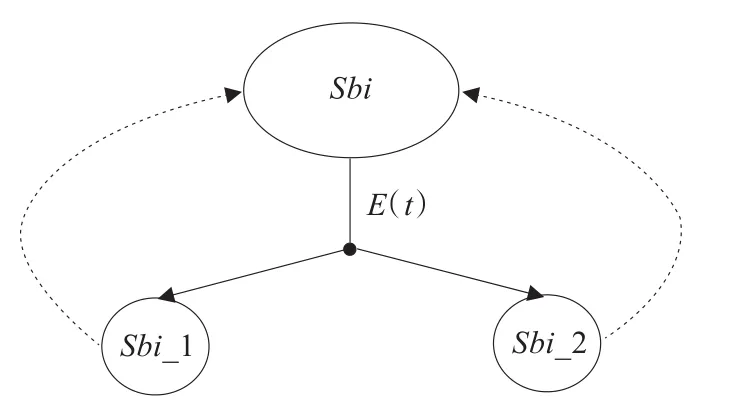
图2 多子种群的示意图

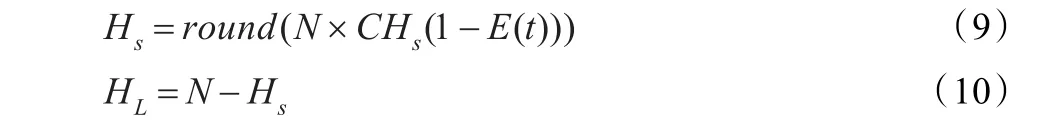
式中，E(t)为子种群进化因子，CHs为探索常数，Hs为探索子群；HL为利用子群。

种群进化因子E(t)定义如下：

从式（11）可知，当E(t)＞0时，粒子群处于进化状态；当E(t)=0时，粒子群进化处于停滞状态，因此，通过E(t)适应确定探索粒子，保证“利用”和“探索”间平衡，克服PSO算法存在的不足，提高粒子群的搜索能力。

2.2.3 MPSO算法对误差的修正步骤

步骤1把未知节点的每一个可行解看作粒子，在网络通信区域对每一个未知点的可解解速度和位置初始化，并设置粒子群算法的相关参数。

步骤2根据式（12）计算每一个粒子的适应度值，将最优粒子的位置保存 pi中，粒子群体最优位置保存 pg中。粒子适应度函数定义为：

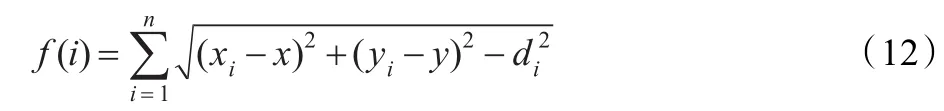
步骤4根据适应度值对粒子进行排序，选择前HL个粒子组成“利用”子群，其余粒子组成“探索”子群。

步骤5根据式（7）、（8）更新粒子的速度和位置，并调整权重。

步骤6将每个粒子的位置与自身的历史最优位置 pi比较，如果优于 pi，该粒子位置代替自身历史最好位置 pi。

步骤7将每个粒子的位置与种群的历史最优位置比较 pg，如果优于 pg，该粒子位置代替种群历史最好位置 pg。

步骤8根据式（12）计算新粒子群的适应度值。

步骤9如果达到算法的终止条件，停止优化，不然根返回步骤4继续优化。

步骤10输出全局最优粒子的位置对应坐标(x，y)。

3 仿真实验

3.1 实验场景

整个教学过程中，发现学生的学习兴趣一直没有衰减，面对问题，能层层去解决，表现出良好的秩序感，课堂气氛和谐而不呆板，学生根据自己的能力，各司其职，井井有条。

假设节点随机分布在400 m×400 m二维区域内，节点总数为200，信标节点为40，未知传感器节点的位置随机产生，传感器节点的通信半径均为20 m，限定门限值M=4，在MATLAB 2008平台上实现传感器节点定位算法。

3.2 对比算法和评价指标

为了使MPSO-DV-Hop算法的定位结果更具说服力，采用DV-Hop算法、粒子群优化DV-Hop算法（PSO-DV-Hop）进行对比实验。算法的性能评价指标为平均定位误差（ave_error），其计算公式为：

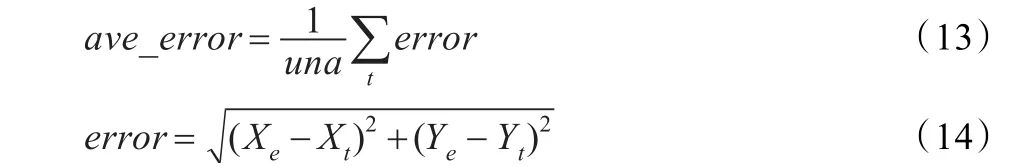
式中，una是未知节点的个数，error为每个未知节点的定位误差，(Xe，Ye)、(Xt，Yt)分别是未知传感器节点估计值和真实值。

3.3 跳数门限值的设定

设M=3、5、7，在不同的信标节点个数条件下，MPSO-DVHop的仿真结果如图3所示。从图3中可知，在相同的信标节点，跳数的门限值M越小，MPSO-DV-Hop算法的传感器节点的定位误差相应越小，这表明，通过合理设置传感器节点间跳数门限值，传感器传节点的定位精度得到提高。因此本文的跳数门限值M=3。

图3 M值对定位误差的影响

3.4 结果与分析

3.4.1 粒子群算法改进的有效性

设定位目标误差为0.05 m，MPSO-DV-Hop、PSO-DV-Hop定位误差与迭代次数关系如图4所示。从图4可知，MPSODV-Hop只要经过10次迭代就可以达到传感器节点定位精度要求，而PSO-DV-Hop要进行35次以上的迭代才能得到传感器节点定位精度要求，这表明MPSO算法通过引入“多子种群”机制，具有更优的全局搜索能力，使算法的计算工作量大大减少，对于能量受限的WSN具有重要意义。

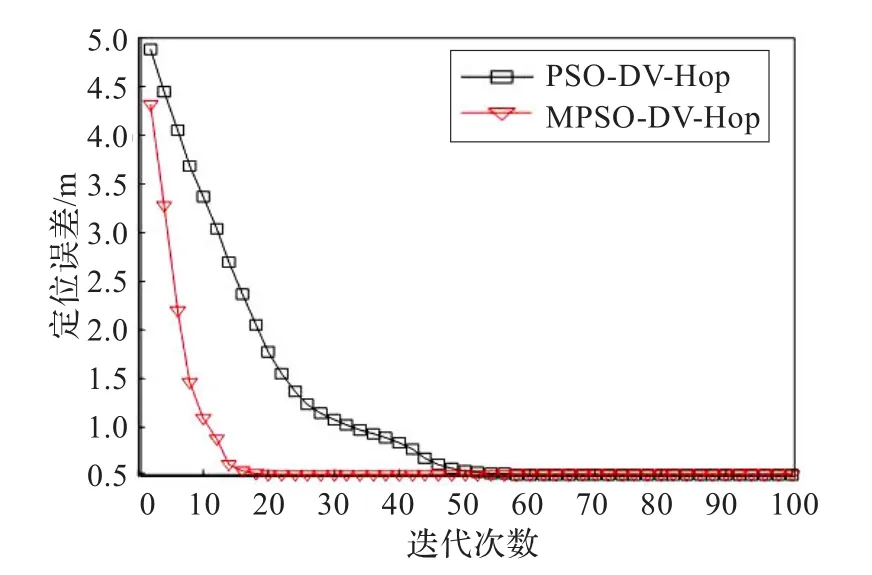
图4 粒子群算法改进前后的定位误差比较

3.4.2 不同信标节点下的定位性能比较

在不同的信标节点下，DV-Hop、MPSO-DV-Hop、PSODV-Hop算法的传感器节点平均定位误差如图5所示。从图5可知，当信标节点数量较少时，3种算法的平均定位误差都较大，随着信标节点数量的增加，传感器节点平均定位误差开始递减，在相同的信标节点下，PSO-DV-Hop的算法优于经典DV-Hop算法；相对于PSO-DV-Hop的算法，MSPO-DV-Hop算法的平均定位误差明显减小，尤其当信标点数量少时，MSPO-DV-Hop算法定位精度的提高幅度明显优于对比算法，这一点非常符合无线传感器网络的需求，信标节点的定位需求越少，人力物力成本则会降低。

图5 不同信标节点下的3种算法的定位误差

3.4.3 不同通信半径下的定位性能比较

在不通信半径情况下，DV-Hop、MPSO-DV-Hop、PSODV-Hop算法的传感器节点平均定位误差如图6所示。从图6可知，随着通信半径的增加，由于未知节点的可定位信标节点数增加，同时信号强度增加，测距更加准确，DV-Hop、MPSO-DV-Hop、PSO-DV-Hop算法的传感器节点平均定位误差逐渐减小，但在相同的通信半径下，相对于DV-Hop、PSO-DV-Hop算法，MPSO-DV-Hop提高了传感器的平均定位精度。

4 结束语

通过对无线传感网络DV-Hop定位算法的分析，针对其不足，提出了一种MPSO算法优化DV-Hop的传感器节点定位算法。改算法的核心思想是：修正节点间的跳数门限值，并结合了MPSO算法解决约束优化问题的优点对传感器定位结果进行修正，该法实现简单，不需增加额外的设备，仿真结果表明，MSPO-DV-Hop提高了传感器节点的定位精度，尤其在信标节点少、通信半径较小的情况下，优越性更加明显。

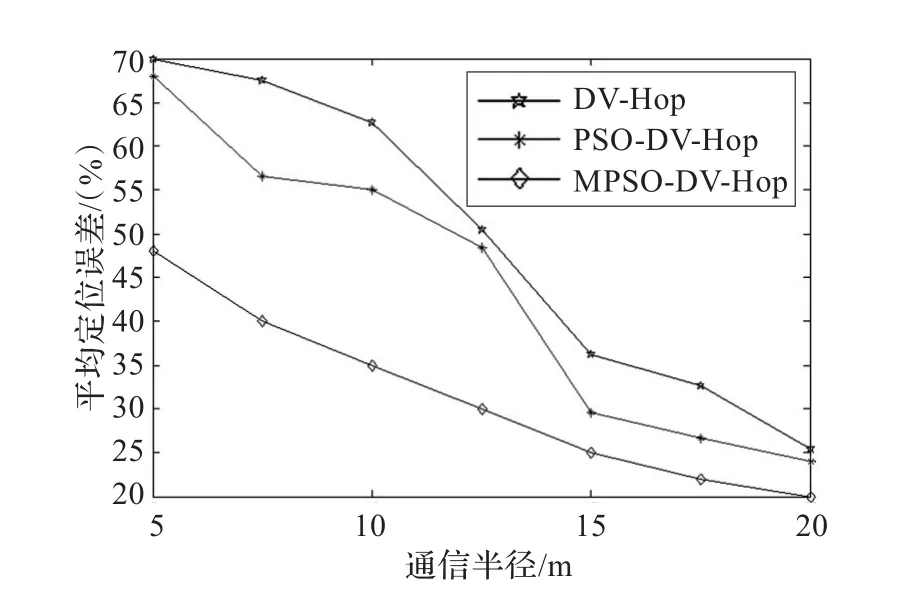
图6 三种算法在不同通信半径下的误差

[1]王福豹，史龙，任丰原.无线传感器网络中的自身定位系统和算法[J].软件学报，2005，16（5）：857-868.

[2]CostaJ A，PatwariN，Hero O.Distributed weightedmultidimensional scaling for node localization in sensor networks[J].ACM Transactions on Sensor Networks，2006，2（1）：39-64.

[3]Minh N，Duc V，Challa S，et al.Nonnumeric MDS for sensorlocalization[C]//3rd InternationalSymposium on Wireless Pervasive Computing，2008：396-400.

[4]刘运杰，金明录，崔承毅.基于RSSI的无线传感器网络修正加权定位算法[J].传感技术学报，2009，23（5）：717-721.

[5]安恂，蒋挺，周正.一种用于无线传感器网络的质心定位算法[J].计算机工程与应用，2007，43（20）：136-138.

[6]周彦，文宝，李建勋.无线传感器网络节点近点加权质心定位方法[J].计算机工程与应用，2012，48（1）：87-89.

[7]肖玲，李仁发，罗娟.基于非度量多维标度的无线传感器网络节点定位算法[J].计算机研究与发展，2007，44（3）：399-405.

[8]LorinczK，Welsh M.A robustdecentralized approach to RF-based location tracking[C]//Proceedings of International Workshop on Location and Centex Awareness.Berlin，Germany：Springer-Verlag Press，2005：63-82.

[9]赵仕俊，孙美玲，唐懿芳.基于遗传模拟退火算法的无线传感器网络定位算法[J].计算机应用与软件，2009，26（10）：189-192.

[10]邓力.基于遗传算法WSN节点定位算法研究[J].计算机仿真，2011，28（9）：161-164.

[11]孙泽宇，魏巍.一种改进无线传感器网络定位算法的研究[J].计算机仿真，2010，27（9）：125-127.

[12]林金朝，刘海波，李国军，等.无线传感器网络中DV-Hop节点定位改进算法研究[J].计算机应用研究，2009，26（4）：1292-1295.

[13]吴黎爱，周力.无线传感器网络中一种修正DV-Hop算法[J].计算机系统应用，2012，31（4）：922-924.

[14]陈星舟，廖明宏，林建华.基于粒子群优化的无线传感器网络节点定位改进[J].计算机应用，2010，30（7）：1736-1739.

ZHOU Tianqi1,JIANG Fengru2

1.Department of Computer and InformationTechnology,Zhejiang Changzheng Professional&Technical College,Hangzhou 310023,China 2.Department of Applications Electronics,Henan University of Animal Husbandry and Economy,Zhengzhou 450044,China

Localization is one of most important technolony of wireless sensor network,in order to reduce the error of node localization for DV-Hop algorithm in wireless sensor networks,a node localization algorithm based on Multi-population Particle Swarm Optimization（MPSO）algorithm and DV-Hop algorithm is proposed.The hops between nodes are modified by threshold value to improve the estimating accuracy of the hop distance,and then in the third stage of DV-Hop algorithm which MPSO algorithm is used to correct the localization error,the simulation analysis of MPSO-DV-Hop algorithm is carried out on MATLAB2008.The results show that the algorithm can improve the localization accuracy of the sensor without increasing cost situation.It has a high pratical value.

wireless sensor network;node localization;Multi-subpopulation Particle Swarm Optimization（MPSO）algorithm; DV-Hop algorithm

节点定位技术是无线传感器网络的关键技术，为减小DV-Hop算法的节点定位误差，提出一种多子群粒子群（MPSO）算法优化DV-Hop的节点定位算法（MPSO-DV-Hop）。通过设置门限值修正节点间的跳数，提高了跳段距离估算精度，DV-Hop的第3阶段引入MPSO算法，对节点定位误差进行校正，通过引入多子群加快算法收敛速度，提高DV-Hop算法的节点定位精度，在MATLAB2008平台上对算法仿真分析。结果表明，MPSO-DV-Hop算法在不增加成本情况下，提高了传感器的节点定位精度，具有较高的应用价值。

无线传感网络；节点定位；多子群粒子群优化算法；DV-Hop算法

A

TP391.9

10.3778/j.issn.1002-8331.1305-0390

ZHOU Tianqi,JIANG Fengru.Node localization of wireless sensor network based on MPSO-DV-Hop.Computer Engineering and Applications,2013,49（23）：52-55.

周天绮（1976—），男，讲师，研究方向为计算机网络；姜凤茹（1978—），女，讲师，研究方向为信号处理。E-mail：zhoutianqi_2012@126.com

2013-05-29

2013-07-15

1002-8331（2013）23-0052-04

CNKI出版日期：2013-07-22 http://www.cnki.net/kcms/detail/11.2127.TP.20130722.0921.002.html