小波SVM核函数法在滚动轴承故障诊断中的应用
高朋飞, 许同乐,侯蒙蒙,郎学政,李磊
(1.山东理工大学 机械工程学院,山东 淄博 255049;2.山东信远集团有限公司,山东 莱阳 265200)
故障轴承的振动信号包含了故障特征信息,而且便于采集,因此振动信号分析成为故障诊断的有效手段之一[1-3]。小波分析不仅能对振动信号进行降噪处理,还能对信号进行进一步分解,提取不同频段的故障特征,在信号处理领域得到了广泛应用。支持向量机(Support Vector Machine,SVM)是一种基于统计学理论的模式识别方法,其克服了神经网络结构选择困难、容易陷入局部极小值等问题,并能很好地解决小样本学习问题,已应用于许多领域[4-7]。
在此,提出了一种基于小波分析的SVM滚动轴承故障诊断方法,通过小波分析提取轴承的尺度能量谱,建立故障特征向量集,然后将其作为SVM的训练样本,并用改进的SVM核函数进行训练,获得故障分类模型,最后用该分类模型对未知故障信号进行预测分类。
1 基于小波分析的故障特征提取
采用小波阈值方法进行降噪,对降噪后的信号进行小波变换,可以得到信号的故障特征。设f(t)为有限能量函数,即f(t)∈L2(R),则该函数的小波变换定义为
(1)
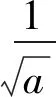
根据能量守恒可得
(2)
式中:Cψ为小波的容许条件;ω为频率。
则f(t)在尺度a上的能量为
(3)
E(a)称为尺度-小波能量谱,它反映了信号能量随尺度的变化情况。
为了更好的分析和表征信号的能量特征,采用各个频段能量在总能量Esum中所占的比例A(i)作为故障特征向量。选取所需要的频率段信号,提取其尺度-小波能量谱并计算该能量大小,记为Ei,则
(4)
2 SVM故障分类器设计
2.1 支持向量机原理
支持向量机方法建立在统计学习理论的VC维理论和结构风险最小原理基础上,它根据有限的样本信息在模型的复杂性与学习能力之间寻求最佳折中,使结构风险最小,即同时最小化经验风险和VC维的界,以获得最好的泛化能力[7-9]。
以二分类为例,给定训练数据样本集:(xi,yi),i=1,2,…,n;x∈Rd,y∈{+1,-1}。其中n为训练样本数,d为每个训练样本向量的维数,y为分类标号。如果该样本能被一个超平面线性分开,则该分类超平面的方程为wx+b=0,其中w为权系数向量,b为分类阈值。需要找到最优超平面,使训练集中的所有样本均能被该超平面正确分开,而且支持向量与超平面之间的距离最大[9]。
在线性可分的情况下,求最优分类面可转化为在满足yi(wxi+b)≥1的条件下求w2/2的最小值问题。此问题可以通过求解Lagrange函数得到解决,进而得到最优分类函数为
(5)
式中:αi为Lagrange乘子。根据f(x)的值就可以判断x所属的分类。
对于非线性分类,可以使用一个非线性映射Φ把数据样本从原空间Rd映射到一个高维特征空间Ω,再在Ω中求最优分类面。根据泛函有关理论,只要一种核函数K(xi,xj)满足Mercy条件,它就可以对应某一变换空间的内积,这样在高维空间实际上只需进行内积运算,而这种内积运算是可以用原空间中的函数实现的,无需知道变换Φ(x)的具体形式。此时,最优分类面的形式为
(6)
在机械设备故障诊断中,简单的二分类显然不能满足工程实际要求,因此需要支持向量机的多分类模型,可以分别用多个二分类器进行训练,得到多分类模型。
2.2 新核函数
一个好的核函数不仅能够解决样本低维线性不可分的问题,还能在一定程度上优化SVM训练算法,缩短样本训练时间。因此,选择合适的核函数是建立最优SVM模型的关键,直接影响模型的训练精度、训练速率和泛化能力[10]。目前,如何选取核函数还缺乏统一的理论指导,比较常用的核函数有4种:
(1)线性核函数,K(x,y)=xy,就是线性支持向量机采用的核函数。其仅适用于简单的线性分类问题,无法解决大多数复杂的非线性分类问题。
(2)多项式核函数,K(x,y)=(xy+1)d,其中d=1,2,3…,为多项式的阶数。在特征空间维数很高时,该核函数的d值很大,将使计算量大大增加。
(3)Sigmoid核函数,K(x,y)=tanh[v(xy)+c],其中v,c分别为比例、偏移参数。其必须在某些特定条件下才满足对称、半正定的核函数条件,在应用上受到一定的限制。
(4)径向基核函数,K(x,y)=exp{-x-y2/2σ2},其中σ为函数的宽度参数。径向基核函数最为常用,但σ的不同取值直接影响向量机的支持向量个数和训练得到的超球面的形状,容易产生超球面空间不稳定和泛化能力降低等问题,而且对于不同的训练样本,问题的出现形式也不同,其应用也存在一定的局限性。
为此,提出一种新的核函数
z=max‖x-y‖。
(7)
新核函数满足Mercy条件且结构形式简单,当训练样本维数较多时,计算量也较小。而且核参数z不需赋值,而是取决于数据样本,可以根据样本输入自动调整,实现自适应训练,解决了径向基核函数中σ的选择问题,适用于大部分复杂非线性分类问题。
为验证新核函数的优越性,对不同核函数的SVM模型进行了仿真分析。由仿真结果可知,与其他核函数相比,新核函数显著提高了训练精度,预测分类准确率也较高,说明该模型有较好的学习能力和泛化能力。
2.3 小波尺度-能量谱SVM故障诊断模型
小波尺度-能量谱SVM故障诊断的原理图如图1所示,首先,对获得的故障振动信号进行预处理,应用小波分析进行降噪,对降噪后的信号进行小波分解与重构,提取故障信号的小波-尺度能量谱,并建立故障特征向量集;然后,以此特征向量集作为SVM训练的输入样本,应用提出的新SVM核函数对故障特征进行训练,通过调节参数使准确率符合要求,继而建立SVM故障诊断模型;最后,将未知样本数据输入诊断模型,再进行预测分类并输出相应的诊断结果,从而实现滚动轴承的故障诊断。

图1 小波尺度能量谱SVM故障诊断原理
3 试验验证
3.1 信号提取
试验轴承型号为6004zz,内径为20 mm,外径为42 mm,宽度为12 mm,钢球个数为9,钢球直径为6.35 mm。外圈固定,内圈旋转。故障模式为单一故障,其中内圈与外圈故障为裂纹,分布在沟道处,长约1 mm;钢球故障是在其表面切掉了一小部分,不影响正常滚动。
在试验台轴承基座的水平方向和垂直方向上布置2个振动测试点,加速度传感器安装在电动机驱动端,测量轴承振动加速度信号。为获取轴承故障的相关数据,试验台上分别进行了正常及3种典型故障的模拟试验。试验数据均进行多次采集,试验采样频率为12 kHz,轴承转速为1 750 r/min。
轴承振动信号的时域图如图2所示,可以看出,故障信息非常不明显,基本上都被噪声淹没,无法识别是否存在故障以及故障类型。如果对其直接进行频谱分析,诊断效果不是很好。
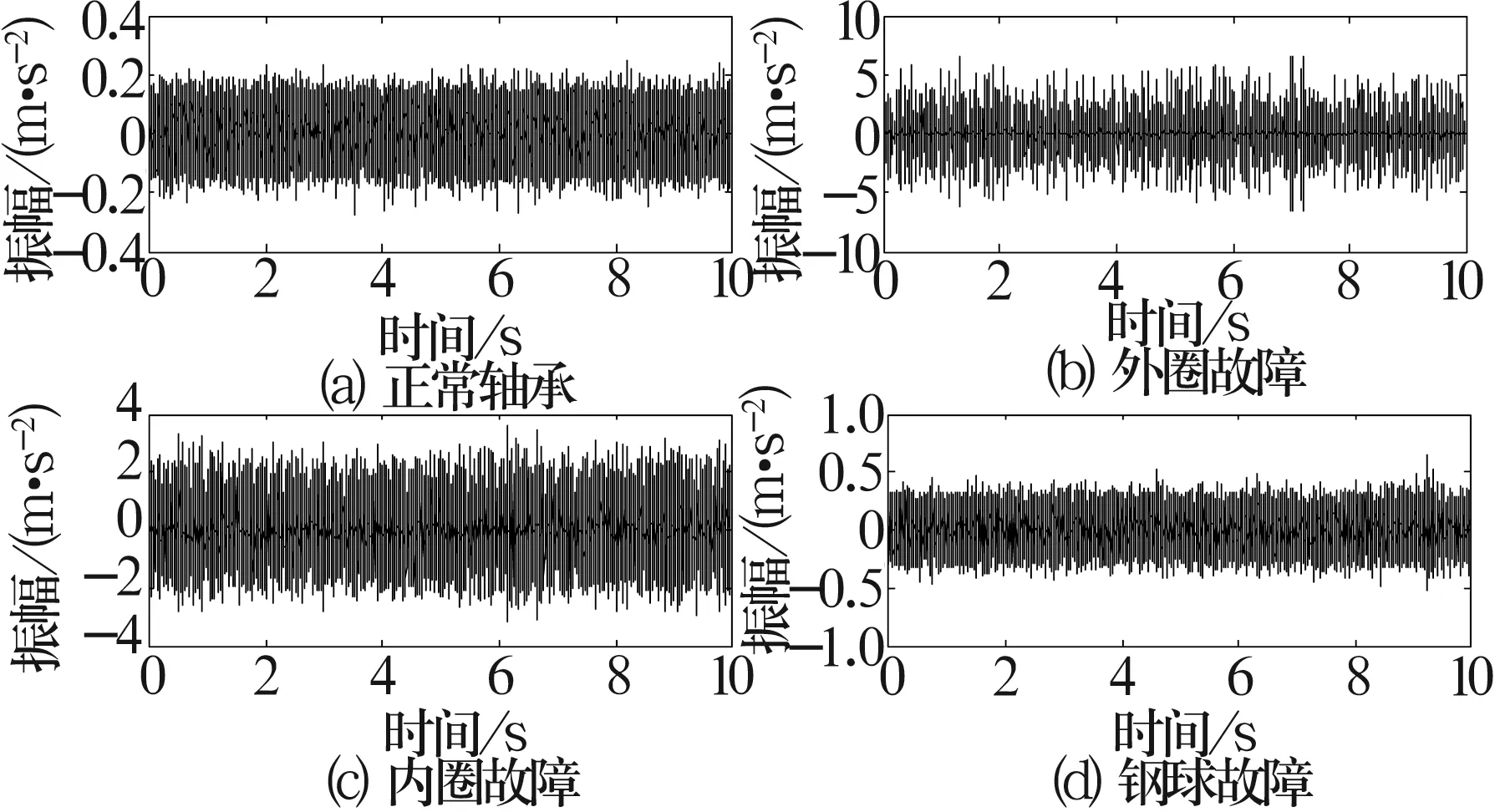
图2 不同故障类型轴承的振动信号
对振动信号进行预处理,应用小波阈值方法对振动信号降噪,去除大部分噪声;然后采用db4小波基对信号做4层小波包分解,得到表征故障特征的尺度能量谱,也就是信号的能量系数比,如图3所示。
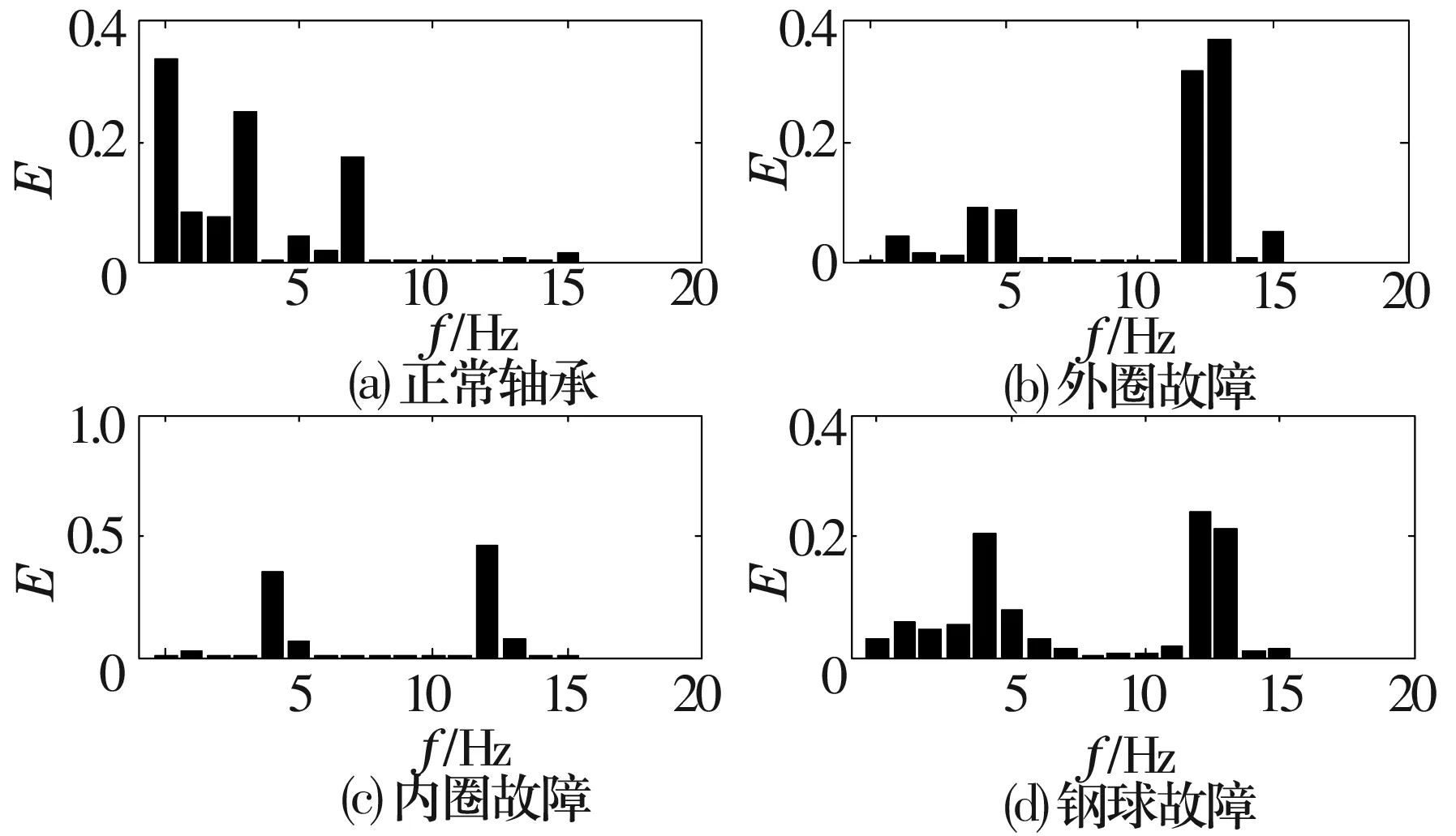
图3 不同故障类型轴承的故障特征对比
由图3可知,不同故障的能量特征谱有明显的差别。正常轴承的能量大多分布在低频段,高频段能量很小;外圈故障轴承由于受到振动冲击,在高频段有很高的能量,低频段也有小部分能量;内圈故障轴承的高、低频段各有一部分能量,但能量分布比较集中;钢球故障轴承在高频段能量分布较集中,低频段能量分布则趋于分散;因此,提取轴承各个频段的能量,将其进行归一化等处理后作为故障特征向量集,然后应用SVM方法可以对故障特征进行预测和分类。
3.2 数据处理
为避免样本数据差距过大对分类预测的影响,必须对样本数据进行归一化预处理,将其线性调整到[-1,+1]区间。
随机选取参数是利用程序随机选取惩罚参数和核参数,当有多组惩罚参数对应于最高分类准确率时,选取最小的一组作为最佳惩罚参数,因为过高的惩罚参数会导致过学习状态的发生,即训练集分类准确率很高而测试集分类准确率很低,也就是说分类器的泛化能力降低。
为了得到比较理想的分类准确率,采用交叉验证(Cross Validation,CV)的方法对惩罚参数和核函数参数进行寻优,选取准确率最高的一组作为模型的参数。交叉验证即将原始数据分为训练集和验证集2组数据,依次使用训练集和验证集对分类器进行训练和验证,以分类准确率作为分类器的性能指标。
从轴承故障信号中选取320组数据。其中160组数据(每种故障类型选取40组)作为故障的训练样本,剩余160组数据作为测试样本。为验证新核函数分类模型的学习能力和泛化能力,分别应用新核函数和径向基核函数进行训练,然后再用测试样本进行检验。结果见表1。

表1 不同核函数SVM诊断模型的分类准确率
从表1可知,对于径向基核函数SVM模型,未经优化训练的分类模型由于发生了过学习和欠学习,预测准确率不高,为80%左右;而采用CV进行参数优化后,准确率稍有提高,但仍不足以用于模式识别与故障诊断。
而新核函数在样本维数较多时,有很好的空间稳定性。表中未优化参数时,准确率同样不高;而优化后的参数训练模型的分类准确率有显著提高,160个样本中仅有11个样本被误识别。由此可见,新核函数训练得到的模型不仅有很好的学习能力,也具有较好的容错能力和泛化能力,在故障分类方面比径向基核函数更优越。
4 结束语
利用提出的新SVM核函数进行训练,并采用交叉验证的方法对训练参数进行寻优,有效的克服了过学习和欠学习的发生,并获得了更高的准确率,更好的学习能力和泛化能力,能够有效的对轴承故障进行分类。但是对于工业环境中的故障轴承而言,故障振动信号本身具有复杂性,该方法能否准确诊断还需作进一步研究。

