轴向磁轴承涡流损耗分析

胡小飞，刘刚，孙津济，韩邦成

(1. 惯性技术重点实验室，北京 100191；2. “新型惯性仪表与导航技术”国防重点学科实验室，北京 100191)

与传统机械轴承相比，磁轴承具有无接触、无润滑、无磨损、功耗低而且允许转子高速旋转等特点。由于磁轴承的这些特殊性能，使得其在高速电动机、飞轮等领域得到越来越多的应用[1-2]。但是，磁轴承比机械轴承增加了额外的铁耗和铜耗。由于轴向推力磁轴承的实铁芯结构和高频工作特性，定子和推力盘上会产生过大的铁芯损耗，且以涡流损耗为主。另外，磁轴承铁耗过高会产生大量的热量，导致铁芯温度升高，对磁轴承系统的可靠性、稳定性及动态性能等有多方面的影响[3]。因此必须建立轴向磁轴承涡流损耗的分析模型，对涡流损耗进行分析研究。

国内、外众多学者对实心结构磁轴承的涡流问题进行了相关研究。文献[4-5]在Meeker模型的基础上假定了边界条件平均化，给出了纯电磁径向磁轴承旋转转子涡流损耗的电磁场解析模型。但该损耗模型用于分析由于转子旋转引起的涡流损耗，而轴向磁轴承涡流损耗主要是由于控制电流交变及推力盘的轴向振动引起的，因此该损耗模型并不适用于轴向磁轴承。文献[6]采用磁路分析方法给出了实心推力磁轴承转子涡流损耗的解析计算方法。但由于解析计算时，假设铁芯和气隙处的磁场均匀分布，并忽略了铁芯的磁压降，因此模型计算误差较大。

文献[7-9]采用有效磁阻的理论对环形定子结构的磁悬浮装置因控制电流变化和气隙变化引起的涡流效应进行了分析，并且运用有效磁阻的简化模型很好地分析了磁悬浮装置的动态电流刚度和动态位移刚度。文献[10]对有效磁阻模型做了进一步简化，并与有限元分析模型进行了比较，表明了有效磁阻等效的准确性。但上述文献都没有对装置的铁芯涡流损耗问题进行研究。

文献[11]在文献[10]的基础上建立了轴向推力磁轴承涡流损耗的解析模型，对磁轴承的磁通、线圈阻抗及涡流损耗进行了分析。但是该解析模型只分析了控制电流变化引起的涡流损耗，而没有对推力盘轴向振动引起的涡流损耗问题进行研究。由于推力盘的轴向振动会引起轴承气隙长度的变化，从而导致铁芯中磁场的交变，其产生的涡流损耗将随着振动频率的增大而增大，因此必须对推力盘轴向振动引起的涡流损耗问题进行研究。

下文针对磁轴承推力盘沿轴向高频振动时产生的铁芯涡流损耗，提出了一种基于有效磁阻法和等效磁路法的涡流损耗的磁路计算模型。采用FLUX有限元软件分别建立不考虑与考虑漏磁、磁化曲线饱和及边缘效应的有限元模型，并将有限元分析结果与解析模型的分析结果进行比较。

1 磁轴承的结构

举例分析的轴向磁轴承系统由两个轴向磁轴承和一个推力盘组成，构成差动控制方式，模型如图1所示。磁轴承定子铁芯的材料为电工纯铁DT4C，推力盘和转轴铁芯材料为40Cr。由于磁轴承结构为轴对称，可以将模型转化为二维模型进行处理。为了简化解析模型，不考虑漏磁、磁化曲线饱和及边缘效应的影响，并假设推力盘在轴向振动，线圈中的电流保持不变。

图1 轴向磁轴承结构示意图

1.1 磁轴承的有效磁阻

当推力盘以平衡位置为中心沿轴向做正弦规律振动时，两个轴向磁轴承与推力盘之间的气隙长度同样以正弦规律变化，从而导致磁轴承和推力盘中磁场的交变，产生的涡流使得磁轴承系统铁芯上的磁阻发生变化。根据文献[8]有效磁阻的分析方法，将由交变磁场在实心铁芯上形成的涡流，以涡流磁阻的形式来等效，然后可根据等效磁路法计算出气隙磁通及磁轴承电磁力。为了得到铁芯上的有效磁阻，将磁轴承按照磁力线的分布情况划分成6个区域，如图2所示。区域1和区域3由推力盘两侧的过渡区域及推力盘与定子铁芯间的气隙组成。在2个区域中推力盘两侧过渡区域上的磁力线沿径向分布，而气隙内的磁力线则平行于轴向。磁力线在区域2和区域5内平行于径向，而在区域4和区域6内则平行于轴向。可得到磁轴承6个区域的有效磁阻

图2 磁轴承磁力线分布图及区域划分图

(1)

表1 磁轴承的有效磁阻

1.2 磁轴承电磁力的解析模型

(2)

式中：A1为内导磁环的截面积；A3为外导磁环的截面积；Rg为磁路磁阻；下标1，2分别表示轴承1和轴承2。

假设磁轴承推力盘的振动没有引起铁芯的涡流效应，不考虑铁芯动态涡流磁阻。磁轴承气隙处的磁通φ1，φ2分别为

(3)

式中：N为单个定子极匝数；I0为线圈电流。其中，

(4)

(5)

可得轴向磁轴承系统的电磁力为

f0sin(ωt)。

(6)

由于上述分析忽略了涡流引起的动态磁阻，由(5)式可知，正弦变化的动态磁通φx会产生涡流，其磁通路径上的有效磁阻不仅包含静态磁阻，还包含涡流形成的等效涡流磁阻，而静态磁通路径上只有静态磁阻。因此，考虑涡流效应的等效气隙磁通为

(7)

其中，

(8)

(9)

可得轴向磁轴承系统的电磁力为

(10)

即f(t)=f0sin(ωt)ψ(ω)，

(11)

其中，ψ(ω)表明了推力盘振动产生的涡流效应，它使得考虑涡流效应后的磁轴承电磁力与不考虑涡流效应的磁轴承电磁力相比，幅值减小且相位滞后。

1.3 磁轴承涡流损耗的解析模型

令函数ψ(ω)的幅值和相位分别为

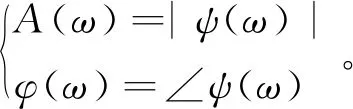
(12)

考虑涡流效应的磁轴承系统的电磁力幅值减小A(ω)，相位滞后φ(ω)，即

f(t)=f0A(ω)sin[ωt+φ(ω)]。

(13)

电磁力所做的功转化为铁芯的涡流损耗，因此轴向磁轴承系统的涡流损耗可表示为

φ(ω)]ωδcos(ωt)，

(14)

可得轴向磁轴承系统的平均涡流损耗为

ωδcos(ωt)dt。

(15)

2 有限元仿真

2.1 磁轴承的二维有限元模型

与有效磁阻法相比，采用有限元法可以考虑漏磁、磁化曲线饱和及边缘效应的影响，能更好地分析磁轴承的电磁力和涡流损耗。

采用有限元分析软件FLUX对磁轴承的瞬态场问题进行仿真分析，铁芯材料的实测非线性磁化特性曲线如图3所示。磁轴承有限元模型如图4所示，是一个二维轴对称模型，并含有一个耦合电路，该电路由2个独立的电流源和电流绞线圈组成。模型中不包含磁轴承转子部分是由于转子与磁轴承定子之间的气隙要比磁轴承气隙长度大得多，可以忽略转子上的漏磁影响。考虑集肤效应，将定子铁芯靠近线圈区域和推力盘外层区域的网格细分。

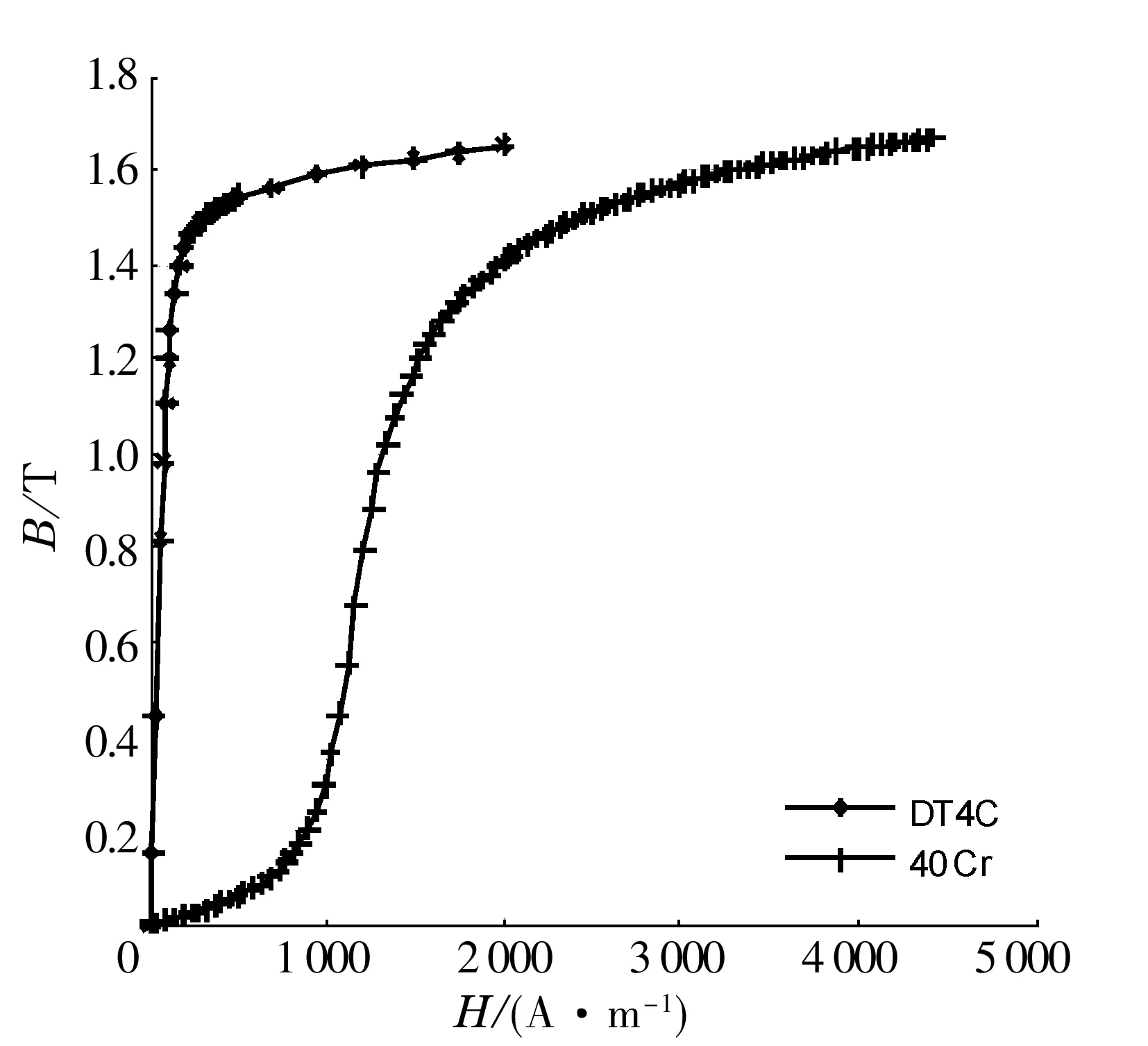
图3 材料的磁化特性曲线

图4 带有耦合电路的磁轴承有限元模型

2.2 电磁力和涡流损耗

进行有限元分析时，保持线圈电流不变，推力盘振动。当气隙长度在点x0处正弦变化时，仿真所得的电磁力f(t)由于与磁密的平方成正比，而且受到漏磁、磁化曲线饱和及边缘效应的影响，不可能与位移一样随时间做正弦变化，因此可对一个仿真周期内变化的电磁力进行离散Fourier变换，分解出一阶线性部分的电磁力。Fourier变换可得

f(t)=f0(ω)+f1(ω)sin(ωt+φ1)+f2(2ω)·sin(2ωt+φ2)+… ，

(16)

取一阶线性部分的电磁力作为有限元仿真所得到的磁轴承的电磁力，即

f(t)=f1(ω)sin(ωt+φ1)。

(17)

磁轴承瞬时单位体积铁芯涡流损耗计算模型为[12]

dP(t)=E(t)J(t)。

(18)

单位体积的平均涡流损耗为

(19)

总的平均涡流损耗为

(20)

式中：E为电场强度矢量；J为电流密度矢量；T为仿真周期。

3 计算结果及其对比分析

用于4 kW磁悬浮高速电动机的纯电磁轴向磁轴承的参数为：r1=28 mm,r2=31.5 mm,r3=40 mm,r4=43 mm,h1=8 mm,h2=17 mm,h3=8 mm,g0=0.4 mm,δ=0.1 mm,N=220,线圈电阻R=4 Ω,40Cr电阻率为0.2×10-6Ω·m，DT4C电阻率为0.12×10-6Ω·m。保持通入磁轴承线圈的偏置电流不变(1.05 A)，推力盘在磁中心位置x0=0.4 mm处做小幅振动，气隙长度的变化值为：x1=x0+δsin(ωt)，x2=x0-δsin(ωt)。在解析模型中，材料采用线性相对磁导率，其中40Cr的线性相对磁导率为400，DT4C的线性相对磁导率为8 000。有限元可以分析铁芯磁饱和效应的影响，材料的相对磁导率用非线性磁化曲线表示，如图3所示。

比较磁路解析模型和不考虑漏磁、磁化曲线饱和及边缘效应的有限元模型的分析结果。进行有限元分析时，不考虑磁化曲线饱和，将材料的相对磁导率设置为线性。为了忽略漏磁的影响，可将磁轴承定子铁芯及推力盘包围的空气区域(除气隙区域)以及线圈区域的相对磁导率设置为接近于0的值，使得磁通不能透入到此区域中，从而不用考虑这部分漏磁的影响。

3.1 不考虑非线性因素影响的电磁力

不考虑漏磁、磁化曲线饱和及边缘效应，有限元分析与解析模型的电磁力频率特性曲线如图5所示。

图5 电磁力的频率特性曲线

从图5可以看出，解析模型所得电磁力频率特性曲线与有限元模型分析的频率特性曲线基本吻合。其中，电磁力幅值最大误差发生在低频段，是由电磁力与位移之间的线性化假设引起的。因为解析法建立电磁力解析模型时认为位移变化的幅值与平衡位置的气隙长度相比很小，忽略其高阶次项，使得电磁力比有限元分析的结果小，但其最大误差不超过3 N。当频率升高时，解析模型与有限元模型分析的电磁力相位误差增大，不过相位角误差不超过3°。因此，不考虑漏磁、磁化曲线饱和及边缘效应，解析模型可以很好地分析磁轴承铁芯的涡流效应。

3.2 考虑非线性因素影响的电磁力

考虑漏磁、磁化曲线饱和及边缘效应的有限元模型与解析模型的电磁力频率特性曲线如图6所示。由图可知，电磁力幅值最大误差也发生在低频段，且由于解析模型不能考虑漏磁、边缘效应等因素的影响，使得误差增大，误差最大为5 N。解析模型得到的电磁力与有限元模型得到的电磁力在高频段存在较大的相位误差，这是因为漏磁削弱了气隙长度变化对磁场的影响，使得铁芯的涡流效应比不考虑漏磁时减小了，且漏磁随频率的增大而增大，从而导致高频段的相位误差较大。

图6 电磁力的频率特性曲线

3.3 涡流损耗

解析模型与有限元模型得到的磁轴承涡流损耗情况如图7所示。不考虑漏磁、磁化曲线饱和及边缘效应的影响，解析模型与有限元模型得到的磁轴承涡流损耗基本相同，高频段的最大误差不超过0.5 W；考虑漏磁、磁化曲线饱和及边缘效应的影响，解析模型计算的涡流损耗比有限元计算的涡流损耗大，且高频段涡流损耗的误差较大。表明漏磁削弱了气隙长度变化对磁场的影响，使得铁芯的涡流减小了，而且频率越高，漏磁越大。因此在涡流损耗分析中不应该忽略漏磁、磁化曲线饱和、边缘效应等非线性因素的影响。但是，当考虑非线性因素时，很难得到电磁力的解析解，只能进行有限元分析，且有限元建模分析较为繁琐，尤其是对磁轴承结构进行优化时，要对不同的情况分别构造分析模型。所以在低频应用场合，或对涡流损耗的计算精度要求不高时，解析模型较为适用。

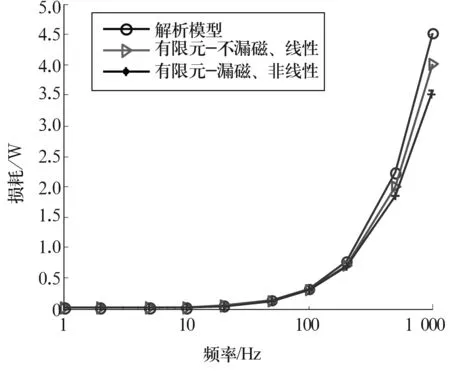
图7 不同频率下的磁轴承涡流损耗

4 结束语

(1)基于有效磁阻法和等效磁路法建立了磁轴承涡流损耗的磁路计算模型，将磁通路径上的铁芯涡流以有效磁阻的形式等效，并建立了动态气隙磁通及电磁力的解析分析模型。解析模型计算结果与不考虑漏磁、磁化曲线饱和及边缘效应影响的有限元计算结果非常吻合，表明了动态涡流磁阻的等效是合理的。

(2)考虑漏磁、磁化曲线饱和及边缘效应的有限元分析结果表明，漏磁削弱了气隙长度变化对磁场的影响，导致解析模型计算的涡流损耗比有限元模型大，且在高频段的误差较大。

(3)磁路解析模型没有考虑漏磁、磁化曲线饱和及边缘效应的影响，在高频段的误差较大，但解析模型能够形象直观地反映磁轴承电磁力及涡流损耗随磁场交变的情况，且模型简单，参数易于修改，可用于低功耗磁轴承结构的优化设计和参数选定。在低频应用场合或对涡流损耗进行估算时，解析模型误差不大，较为适用。