一种噪声优化的900MHz 低噪声放大器设计

康建颖，陈 岚，王海永

(中国科学院微电子研究所，北京 100029)

1 引言

在无线通信系统中，低噪声放大器是收发机中最重要的单元电路之一。因为一方面接收机的灵敏度主要由低噪声放大器的噪声系数和功率增益决定，低噪声放大器的噪声系数显著影响着接收机的整体噪声性能，此外，低噪声放大器的功率增益能明显抑制来自后级的噪声。另一方面，低噪声放大器的线性度对整个系统的线性度起着重要的作用。

在低噪声放大器设计中，往往很难做到功率和噪声同时匹配，这样就会降低接收机的灵敏度，使得接收机的性能变差。设计中往往折衷考虑噪声和增益，为了得到更低的噪声而牺牲电路的增益，或者为了获得高增益而牺牲电路的噪声系数。

设计采用传统的单级cascade 低噪声放大器结构，利用新的优化方法，做到了噪声系数和增益同时匹配，并且得到了良好的隔离度和线性度，噪声系数小于0.2dB，增益20dB。

2 原理及电路分析

2.1 二端口网络的噪声系数

典型二端口网络的等效输入噪声如图1 所示，由等效输入噪声电压和等效输入噪声电流共同组成。是源等效噪声电流。

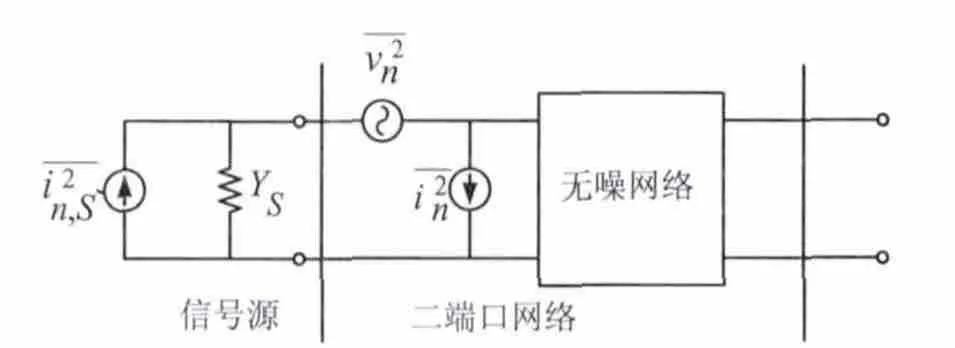
图1 二端口网络的等效输入噪声模型

基于图1的噪声模型，设源导纳为:

并且有如下表达示成立:

进一步可定义相关导纳Yc为:

［1］可知，两端口的噪声系数可表示为:

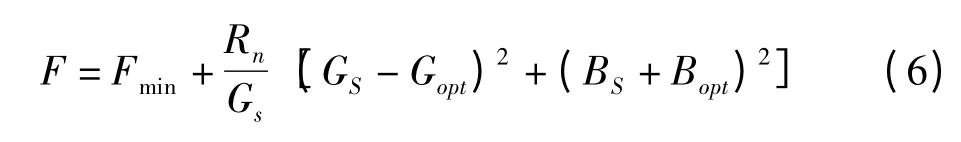
其中，最小噪声系数Fmin和最优源导纳Yout可分别表示为:

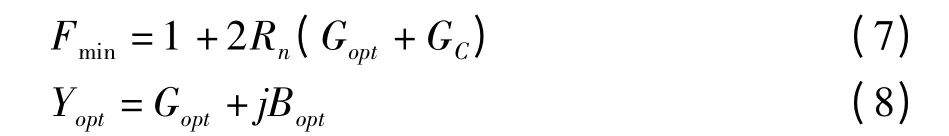
由(1)－(8)式可知，存在最优源导纳，当YS=Yopt=Gopt+jBopt时，可以获得最小噪声系数:

同时，从(7)式可知，即使实现了最优的源阻抗，放大器最终可获得的最小噪声系数还取决于电路本身的噪声电压、噪声电流以及两者的相关性。所以，即使同样的电路结构，优化电路结构中噪声电压和噪声电流之间的相关性也可以优化最小可获得的噪声系数。

2.2 低噪声放大器原理

图2 所示结构是低噪声放大器输入端电路结构，利用源简并电感来得到具有正实部的输入阻抗，并可在功耗限制的情况下得到较优的噪声性能［2］。

图2 源简并低噪声放大器

如图2 所示，ZE是源简并阻抗(通常为电感Lg)，它在晶体管的栅极等效为一个实部阻抗，提供输入阻抗的实部，并且与Lg、Cgs(栅源电容:包括寄生电容和外接电容)谐振，使得输入阻抗的虚部为0，从而实现阻抗匹配。输入阻抗可表示为:

这里，gm表示输入管M1的跨导值，通过合理设计，优化电路结构的噪声电压，噪声电流以及两者的相关性，当Ys=Gopt+jBopt时，可以在功耗限制的情况下取得比较好的噪声性能。

然而，噪声匹配和增益匹配往往不能同时达到，表现在史密斯圆图上就是噪声系数圆和增益圆不能重合，所以需要新的电路结构或者新的电路设计方法来实现噪声和增益同时匹配，在得到最大增益的同时实现噪声系数最小。

3 低噪声放大器设计

设计的900MHz 低噪声放大器主要是满足移动设备的需求。于是，在低功耗前提下，不仅需要小的噪声系数和大的功率增益来满足灵敏度的需求，而且需要高线性度以满足信号大的动态范围。

根据实际系统要求，本设计中要求的LNA 指标如下:

阻抗匹配度:输入，输出均小于－10dB;

增益:大于15dB;

功耗:总电流小于3.5mA;

噪声系数:小于0.8dB;

P1dB:大于－15dBm。

根据上述指标，本文采用共源共栅级联结构的低噪声放大器，这是因为:

1)共栅晶体管可以减小电路输出端电压变化对输入端的影响，提高电路的隔离度。

2)共源共栅结构可以提高电路的输出阻抗，增大电路的增益。

3)共源共栅结构电路可以抑制共源晶体管的米勒效应，提高电路的工作频率。

设计提出的电路结构图如图3 所示。

图3 优化的低噪声放大器电路图

其中:Ldesign是源级负反馈电感，有输入阻抗匹配和噪声匹配的双重作用;Czero是滤波电容;M1和M2是共源共栅晶体管，起放大作用;Lbais是高频扼流圈，是偏置电路的一部分;Lp，out是输出电感负载;Cs1，out和Cs2，out是输出匹配电容;Rp，out是输出电阻，能够稳定电路输出，防止振荡发生，同时能够增加电路的带宽;Cs1，in、Cs2，in和Ls，in是输入匹配网络，采用片外贴片元件实现。

根据Haus's的理论［3］，当电路的源反射系数ΓS与S11的共轭相等，即下式成立时，最小噪声系数与最大增益能同时达到［4］。

要使上式成立，可以采取以下方法对电路的设计进行优化处理:

a.在电流允许的范围内改变电路的偏置电流Id，随着电流的改变，S参数以及ΓS，opt的值会随着改变，当电流为某个合适值时，条件式(12)就会成立，但是此时的电流可能超过电路允许的最大电流;

b.改变器件M1和M2的尺寸，S参数以及ΓS，opt的值也会随着改变，当器件尺寸为某个合适值时，条件式(12)可以成立;

c.添加负反馈部分即负反馈电感Ldesign，这也是最有效的方法，通过改变电感值的大小，可以使电路满足条件式(12)的条件。但是需要注意的是:Ldesign的值不宜过大，否则会影响电路的稳定性。

为了达到最小噪声系数和最大功率增益同时匹配，设计具体的流程如图4 所示。

(1)按照图3 所示电路图搭建仿真电路，在未优化、未匹配的情况下仿真电路的ΓS，opt和S11，在史密斯圆图中观察两点的位置是否实现共轭。

(2)通过上述a－c的优化方法多次迭代仿真，也即通过优化Ldesign，改变Id 和改变器件尺寸使得ΓS，opt和S11在史密斯圆图中近似达到共轭位置。

(3)完成电路的匹配，此时ΓS，opt和S11在史密斯圆图中都移动到接近50 欧姆的位置，通过电路仿真检查电路的性能。

(5)检查电路的带宽是否满足要求，如果不满足设计要求，可以改变输入输出匹配网络的拓扑结构。

(4)检查电路的稳定性。可在电路中增加输出电阻Rp，out来降低输出端的Q 值，提高电路稳定性。

图4 LNA 设计流程

4 电路仿真结果及分析

在本设计中，通过图4的优化设计流程，获得如下结果。同时实现噪声优化和增益匹配的结果如图5 所示:a是匹配前的ΓS，opt和S11在史密斯圆图中的位置，b是匹配之后的ΓS，opt和S11在史密斯圆图中的相对位置。

其它电路指标的仿真结果如图6 所示。获得的电路指标如表1 所示，达到了设计指标，而且具有非常低的噪声系数。

图5 匹配前后ΓS，opt和S11在史密斯原图中相对位置的变化

图6 电路仿真结果

表1 电路仿真结果

5 结束语

设计完成了一款900MHz的低噪声放大器，采用最少的片外匹配元件，在很低的工作电流下，实现了约20dB的功率增益和小于0.2dB的噪声系数。高增益有利于抑制后续电路对整个系统的噪声贡献，降低系统的噪声系数;低的LNA 输入噪声系数有利于减小系统的总噪声系数，提高系统的灵敏度。

参考文献:

［1］W M Leach，Jr..ECE 6416 Low noise electronic design class notes［M］.Georgia Institute of Technology，Fall 2004.

［2］Li Zhiqun.Introduction to RFICs［D］.Southeast University，2009.

［3］H A Haus，et al.Representation of Noise in Linear Two Ports［J］.Proceedings of the IRE，1960，48(1):69－74.

［4］Richard Chi－ His Li.RF Circuit Design［M］.A JOHN WILEY ＆ SONS，INC.，PUBLICATION，2008.