小波域改进变步长自适应滤波
金晶晶,周兴沛
(中国电子科技集团公司第四十七研究所,沈阳 110032)
1 引言
自适应滤波器具有自动调节自身参数的能力,较传统的固定系数滤波器具有更高的性能。最小均方算法(LMS)是应用最为广泛的典型算法,但其收敛速度对输入向量自相关函数矩阵特征值的分布敏感,收敛精度及对时变系统跟踪速度等对步长大小选取相互矛盾。小波变换具有较好的去相关能力,在很多情况下能使输入信号的自相关矩阵接近对角阵;可变步长算法在收敛过程中动态调整步长大小,使算法有较小的稳态误差。本文提出一种改进的步长因子调整函数,实现了小波域变步长自适应滤波。
2 基于正交小波变换的LMS 自适应滤波
时域LMS 算法的收敛速度受输入信号自相关矩阵条件数的影响很大,正交小波变换可以将信号在频域正交分割,去除原始信号的相关性,并将串行运算转换成并行运算提高算法的收敛速度。利用小波基将自适应滤波器主通道和参考通道的输入信号分别进行J 层正交小波分解,再对误差信号进行小波重构即可实现对主通道信号的正交小波变换LMS 自适应去噪,其原理如图1 所示。由时域LMS算法及图1 可得第j 层正交小波变换LMS 算法为:
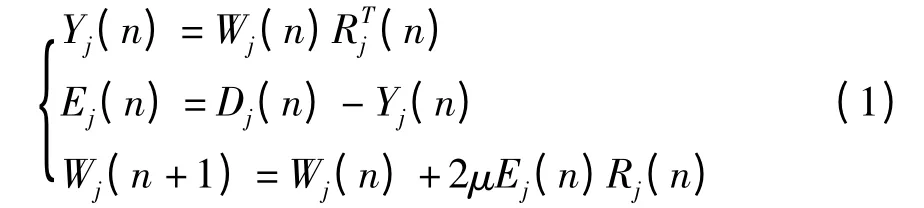
收敛条件是步长因子满足:0 <μ <1/λjmax,λjmax为第j个自适应滤波器输入信号自相关矩阵的最大特征值,j=1,...,J+1为第j个自适应滤波器的阶数。
3 改进的变步长调整函数
传统的固定步长LMS 算法中,收敛速度、收敛精度等与步长大小的选取相互矛盾。类似于Sigmod函数的步长调整函数,使算法同时获得较快的收敛速度和较小的稳态误差[1],通过当前误差和上一步误差的相关估计可动态改变步长调整函数中的参数值,但不能完成所有条件下的参数自适应调整[2-3]。本文提出一种改进的变步长调整函数,其形式为:
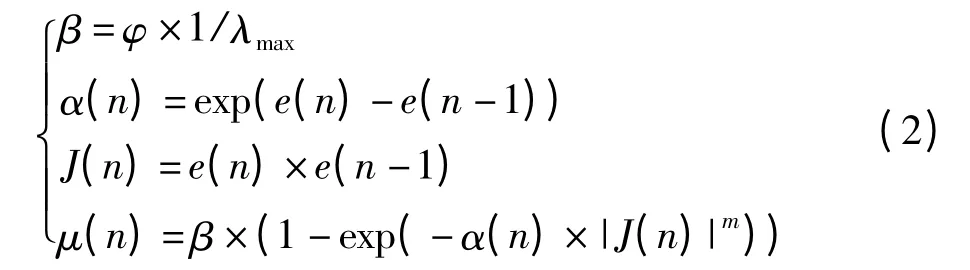
其中0 <φ <1,λmax为自适应滤波器输入信号自相关矩阵的最大特征值,J(n)为当前误差与上一步误差的自相关估计,m为调整参数。将式(2)与式(1)结合即得到正交小波变换的变步长LMS 算法。
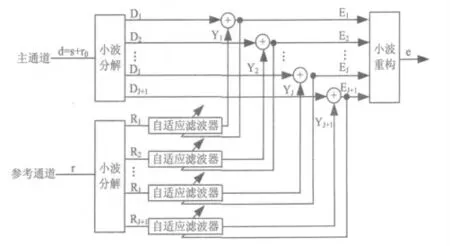
图1 正交小波变换的LMS 自适应去噪原理
改进的变步长调整函数有以下优点:①利用输入信号自相关矩阵的最大特征值确定β,保证了算法的收敛性。②采用指数形式更新α 值,避免了在误差为零时需要重新设定初值的情况。③在初始收敛阶段,误差的自相关估计较大,算法有较大的步长,较快的收敛速度;当接近稳态时,误差的自相关很小,算法有较小的步长,达到很小的稳态误差。
4 实验分析与结论
根据参考文献[4]的模型,将一段心冲击图信号作为主通道信号,如图2(a)所示,选择db2 小波基对参考通道信号进行2 层小波分解。小波分解后输入信号与阶数分别为8 和4的时域自适应滤波器的条件数对比如表1 所示。自适应滤波器输入信号的条件数较小波变换前有所下降,证明了小波变换的去相关能力。
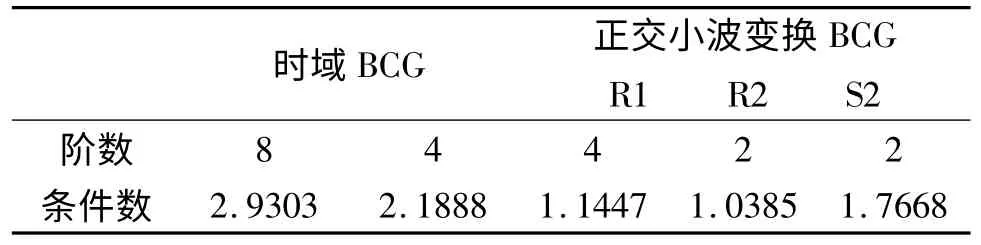
表1 正交小波变换前后自适应滤波器输入信号条件数
分别利用时域LMS 自适应滤波及本文所提方法对这段心冲击图信号进行处理,结果如图2 所示。
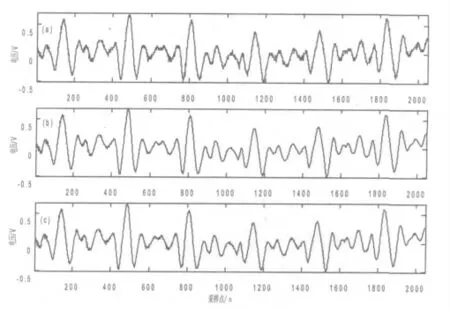
图2 小波变换与时域LMS 自适应滤波去噪结果比较
与原始BCG 信号对比,两种方法都可以去除噪声。以第600 点处作为参考点,比较两种方法处理后信号达到稳态的时间,利用本文所提方法处理后的信号在该点的波形非常平滑,但时域LMS 自适应滤波方法还需要进一步的调整才能达到稳态。因此在收敛速度上,小波域改进变步长自适应滤波算法具有明显的优越性。
[1]高鹰,谢胜利.一种变步长LMS 自适应滤波算法及分析[J].电子学报,2001,29(8):1094-1097.
[2]兰瑞明,唐普英.一种新的变步长LMS 自适应算法[J].系统工程与电子技术,2005,27(7):1307-1310.
[3]孙恩昌,李于衡,张冬英,等.自适应变步长LMS 滤波算法及分析[J].系统仿真学报,2007,19(14):3172-3175.
[4]任济生,任鹏,吉爱国,等.基于正交小波变换的自适应语音消噪改进方法[J].信息与控制,2007,36(4),501-505.

