活动标架的构造及其在模式识别中的应用研究
成丽美,袁伟,姚若侠
陕西师范大学计算机科学学院,西安 710062
活动标架的构造及其在模式识别中的应用研究
成丽美,袁伟,姚若侠
陕西师范大学计算机科学学院,西安 710062
1 引言
活动标架的现代方法是由法国数学家Cartan[1-2]发展起来的,他把前人Cotton、Darboux、Frenet和Serret的工作改造融合,将活动标架发展成为用以研究子流形及其不变量在变换群作用下的几何性质的一种有效工具。到了20世纪70年代,Griffiths[3]、Green[4]、Jensen[5]试图将Cartan的直观构造方法归约为坚实的理论基础。问题是该方法始终无法从狭窄的欧几里德几何或欧几里德空间流形上的等仿射作用下脱离出来。直到一个概念性的跳跃,那就是“将活动标架理论从对任何形式标架丛或联络的依赖中分离出来,定义活动标架为一个从子流形或者Jet丛(射流丛)到群变换的一个等变映射。”基于此概念,显然活动标架不等同于标架(Moving Frames≠Frames!),这一概念层面的跳跃成为新方法形成的关键。近几年来,Fels和Olver[6-7]建立了活动标架理论的一种新方法,其核心思想是将活标架定义为变换群的一个等变映射。该方法可以被系统地应用于一般的变换群,且所有经典的活动标架都可以用这种方法重新诠释。它通过选择一个恰当的群轨道的横截面(cross-section),并对其进行规范化来构造活动标架,进而求解出微分不变量、微分不变算子和不变微分方程等。这种等变的活动标架方法最重要的贡献就是给出了递归构造算法,它将规范化的和差别化的微分不变量与不变微分形式联系起来。这是一种基于Maurer-Cartan方程和相应结构理论的新的、直接的代数构造方法。正是因为构造的代数性,所以算法可以在符号计算系统Maple或Mathematica上得以实现。这种方法产生的结果可以应用到许多新的领域,如共形不变量以及共形微分不变量[8],不变数值方法[9],计算机视觉,模式识别和对称约化在图像中的处理[10],经典不变理论[11],不变微分问题[12],不变子流形方法[13],Poisson几何和可积系统[14],拉普拉斯微分不变算子[15],相对论中的基林张量不变量和协变量[16-17],李代数不变量,量子力学中的经典子代数[18]等。大家知道,欧几里德群、仿射群以及射影(变换)群作用下的不变量能广泛地应用于图像处理和计算机视觉[10,19-21]。其中,微分不变量的应用是最经典的,例如空间曲线的欧氏曲率和挠率。在进行模型识别时,人们希望在数据库中存储一个图片,然后,不从图像上的离散点的观点出发,而是从不变量的观点去进行比较匹配,以此发现相似的图片。也就是说,对于一个给定的曲线,人们可以选取一些关键点并在其上构造其不变量,以便来获得曲线的局部不变的签名曲线,继而可以得到欧几里德不变签名曲线。然后,通过比较不变签名曲线而不是比较曲线本身来获知曲线是否匹配。
本文将以一个一般的变换群为例来演示新的等变方法,也就是用递归算法构造它的活动标架和微分不变量。为了演示该算法的高效性,文中同时给出了活动标架和微分不变量的经典构造方法。
2 活动标架
文中用G表示一个r维的李群,M表示一个m维的流形[6-7],Jn=Jn(M,p),1≤p≤m表示n阶的Jet丛。此外,由于群变换G会保持相切等价关系,由此可得到在Jet空间Jn上的n阶延拓变换群G(n)。基于这些符号,下面给出一些定义:
定义1给定作用在流形M上的变换群G,一个活动标架是一个光滑的,G等变映射

定义2变换群G有两个自然的作用作用于本身,若其满足关系ρ(g·z)→g·ρ(z),则ρ是左活动标架;若满足关系ρ(g·z)→ρ(z)·g-1,则ρ是右活动标架。
引理1如果ρ~(z)是一个作用在流M上的左活动标架,则ρ(z)=ρ~(z)-1是一个右活动标架,反之亦然。
定理1如果变换群G作用在流形M上,当且仅当G在z∈M点附近的作用是自由和正则的,那么活动标架在点z的一个邻域内存在。
定义3对所有的z∈M,若Gz={g∈G|g·z=z},则Gz为迷向子群。
定义4设G是一个作用于M上的局部变换群:
(1)若所有的轨道作为M的子流形都有相同的维数,则称群G的作用是半正则的。
(2)若群G的作用是半正则的,且对于任意一点,存在任意小的邻域,它与G的任意一条轨道相交于一个连通的子集合,则称群G的作用是正则的[20]。
定义5如果对于所有的z∈M,都有Gz={e},则称该作用是自由的。
2.1 活动标架的基本构造方法
活动标架的基本构造方法是基于Cartan的规范化[1,22],而规范化的实质和关键则是要选择轨道的一个恰当的横截面κ。
定理2设G自由、正则地作用在M上,κ是一个截面,给定点z∈M,设g=ρ(z)是唯一的一个将z映射到截面κ上的群元素,即,g·z=ρ(z)·z∈κ。则ρ:M→G是群作用G的一个右活动标架。
给定M上的局部坐标z=(z1,z2,…,zm),设ω(g·z)是群作用的显式公式,则伴随于一个坐标截面κ={z1=c1,z2=c2,…,zr=cr},r=dimG≤m=dimM,ci是恰当选择的常数。右活动标架g=ρ(z)可由以下步骤得到:
步骤1选取常数c1,c2,…,cr∈ℝ,令变换后的坐标等于这些常数,从而给出规范化方程组:
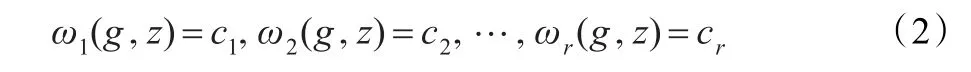
步骤2求解规范化方程组(2),将群元素的参数g=(g1,g2,…,gr)解出,即用z=(z1,z2,…,zm)坐标来表示(g1,g2,…,gr),由此可得活动标架g=ρ(z)。
步骤3将求得的活动标架g=ρ(z)代入剩下的未被规范的变换式ω(g·z)中,会获得群作用的不变量的一个完全系统,也称其基本不变量。
注若ω(g·z)=g·z,则可以获得相应的右活动标架;若ω(g·z)=g-1·z,则可以获得相应的左活动标架。
定理3如果g=ρ(z)是规范化方程组(2)的活动标架解,则函数

构成了一组函数无关的完全的不变量系统,即其基本不变量。
定理4任意一个不变量I(z)可以被唯一地(局部)表示为基本不变量的函数:

定义6假定群G作用在流形M上,那么一个不变量是一个(局部)定义的标量函数F:M→R,它在群G的作用下是不变的,即F(g,z)=F(z),对于使该方程有定义的所有的g∈G,z∈M都是成立的。
定理5一个标量函数I:M→R关于右活动标架ρ的不变性是指不变函数I=ι(F),它满足I(z)=F(ρ(z)·z)。
证明由活动标架的右等价性知:ρ(g·z)→ρ(z)·g-1,因而

大家知道,大部分的群作用不是自由的,因此按照定义,活动标架不存在。不过,有两种方法可以将非自由的群作用转化为自由的。一种是检查群G在流形M的几个副本上的笛卡尔乘积作用,即G×n:M×…×M→M×…×M,由此可获得共形不变量。一种是将群作用延拓到导数空间,即Jet空间[23-24],即G(n):Jn(M,p)→Jn(M,p),由此会导致微分不变量。两种方法的结合则会导致共形微分不变量。

定义9在平面上,如果G不变的曲率κ和它关于G弧长的导数κS被定义,同时在C上是解析的,则曲线C是G规则的;在空间中,如果G不变曲率κ,它关于G弧长的导数κS,G不变率τ和它关于G弧长的导数τS被定义,同时在C上是解析的,则曲线C是G规则的。
定义10非退化G不变平面曲线的G不变签名曲线是由κ和κS参数化的曲线:

非退化G不变空间曲线的G不变签名曲线是由κ、κS、τ和τS参数化的曲线:

因此,签名曲线对于图像识别[4]来说是一个有力的工具,这来源于下面这个定理:
定理6一般的r维变换群G作用于ℝ2,在群G作用下,当且仅当两个G规则的非退化解析曲线C和的签名曲线是相同的,则它们是等价的。
2.2 群作用的延拓
为了给出递归算法的实现,此处对无穷小生成子的延拓做以简要介绍。
定义11设G是一个作用于流形M上的局部变换群,向量场为:

例如,对于平面上的旋转群:

3 递归算法
将r维的李群G作用在m维的流形M上,平凡主丛B=G×M继承了广义群的结构,则有σ(g,z)=z是原映射σ:G×M→M。
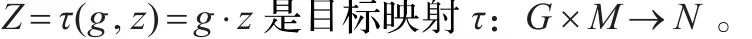
Z(n)=g(n)·z(n),z(n)∈J(n),g(n)∈G是群G的n阶延拓。ν1,ν2,…,νr是群G作用在流形M上的无穷小生成子,它形成李代数g的一个基。μ1,μ2,…,μr是基本的Maurer-Cartan一次形式。
笛卡尔积作用在余切丛T*B≃T*G⊕T*M上,将其分为群和流形两个组成部分,其中群组成部分是由Maurer-Cartan方程的μk展开来表示的,流形组成部分是将局部坐标z=(z1,z2,…,zm)的微分形式dzi代回到流形M上展开来表示的。因此,它导致微分d作用在B上可以将其分成对应的群组成部分和流形组成部分,即d=dM+dG。
通过提升函数f:M→R将其切映射代回到B中,所以λ(f) (g,x)=τ*f(g,z)=f◦τ(g,z)=f(g·z)。此提升函数的原坐标与相应的切坐标的关系Z=g·z可以写成关于群元素和原坐标的函数为Zα=λ(zα),α=1,2,…,m。特别地,提升的微分形式仅仅是由流形组成部分来定义的,即:λ(dω)=dMλ(ω)。
定理8设ω是流形M上的微分形式,则有:

其中,#J是相切形的阶。
注因为在确定活动标架和微分不变量的过程中相切形不扮演任何角色,所以从此处开始,都将它忽略。此外,文中将用“≡”来表示相等的切向模,例如是ω-ς一个相切形,则ω≡ς[25]。
对给定的李群G作用在流形M上,提升水平标架是由因变量的切向量水平微分形式组成的。即
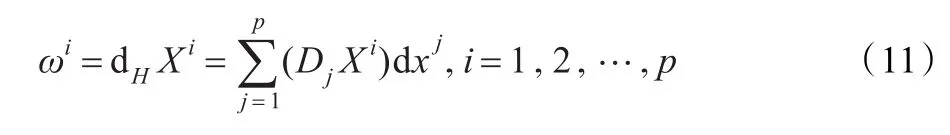
4 例子
构造活动标架有两种方法,一种是用经典的方法即基于Cartan的规范化,另外一种是就是本文的递归算法。通过对通常的微分算子进行不变性处理,可以得到p个互不相关的不变微分算子D1=ι(D1),D2=ι(D2),…,Dp=ι(Dp),它们被迭代地应用到低价微分不变量上,则可以得到高阶微分不变量。下面通过一个例子来演示如何用两种方法来构造活动标架和微分不变量。
4.1 用递归算法构造活动标架和微分不变量
考虑一个作用在流形M=ℝ2上的李群G=ℝ4
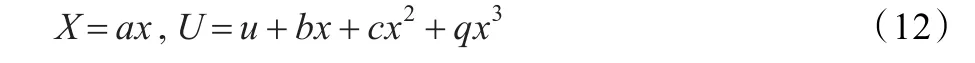
它的延拓无穷小生成子,见表1。

表1 延拓无穷小生成子
由于前述原因,此处不考虑其相切形,那么0阶递推公式为:

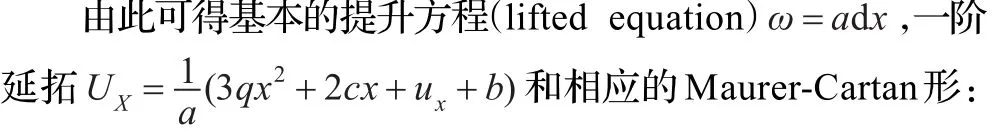

下面开始逐步迭代计算活动标架和微分不变量。
(1)选择0阶横截面κ0={x=1,u=0}。就是说,对于流形M上的点(x,u),要寻找群参数a、b、c、q使得点(X,U)∈κ0。那么其0阶规范化方程组为X=1,U=0,由其解即可得0阶活动标架:
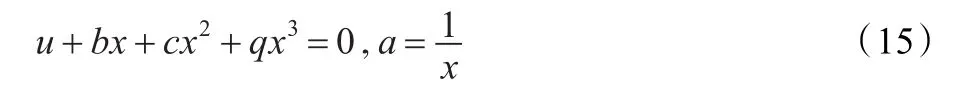


比较等式(20)两边,并利用变换(12)中的X=ax可得2阶延拓:

显然,式(21)中还包含待定群参数c、q,因而它不是微分不变量的最终形式,需要进行第(3)步迭代计算。由2阶规范化方程的隐喻条件dUXX=0可得2阶递推公式:




比较等式(25)两边,并利用变换(12)中的X=ax可得3阶延拓:显然,式(26)中还包含待定群参数q,因而它依然不是微分不变量的最终形式,需要进行第(4)步迭代计算。将式(27)代入到方程(22)、(16)可获得活动标架,即


继而,将式(28)代入到方程(14)中可获得最终的Maurer-Cartan形:

同理,基本微分不变量UXXXX可以通过计算dUXXX=UXXXXω+6μ4来获得。由3阶规范化方程UXXX=0,则存在隐喻条件dUXXX=0,由此得提升不变量为:


4.2用经典方法构造活动标架及微分不变量
考虑一个作用在流形M=ℝ2上的李群G=ℝ4

从方程(33)中可以看出该群含有a、b、c、q四个群参数,用经典方法构造活动标架的实质就是选择一个较好的横截面κ={x=1,ux=uxx=uxxx=0},即,X=1,UX=UXX=UXXX=0。显然,需要由链式法则来分别计算UX,UXX,UXXX:

它和前述方法所得结果式(30)完全相同。此处不再计算其他高阶微分不变量。
5 结束语
本文分别用经典的Maurer-Cartan方法和改进的递归算法构造活动标架和微分不变量。由文中的例子可以看到,用经典的Maurer-Cartan方法构造活动标架和微分不变量时,如果想获得高阶微分不变量,需要用隐式微分逐次迭代来计算高阶微分不变量,且微分阶数越高,尤其是变换越复杂,计算就越困难。而用递归算法构造活动标架和微分不变量,只需要在逐个选择恰当的横截面的同时利用递推公式,即在进行逐步规范化的同时,不但将群参数一个一个确定,也获得了Maurer-Cartan形和微分不变量,从而避免了经典算法所必须的复杂计算。该文用到的递归算法与Kogan[26-28]递归算法相比较,不需要存在一个切片(slice),而且这种递归算法还可以推广应用到无限维李伪群的情形。这些微分不变量的获得可用来构造曲线的局部不变签名曲线,继而可以得到欧几里德不变签名曲线;然后,通过比较不变签名曲线而不是比较曲线本身来获知曲线是否匹配。
[1]Cartan É.La méthode du repére mobile,la théorie des groupes continus,et les espaces généralisés[J].Exposés de Géométrie,1935(5).
[2]Cartan É.La théorie des groupes finis et continus et la géométrie différentielle traitées par la méthode du repére mobile[J]. Cahiers Scientifiques,1937,18.
[3]Griffiths P A.On Cartan method of Lie groups as applied to uniqueness and existence questions in differential geometry[J]. Duke Math Journal,1974,41:775-814.
[4]Green M L.The moving frame,differential invariants and rigiditytheoremsforcurvesinhomogeneousspaces[J]. Duke Math Journal,1978,45:735-779.
[5]Jensen G R.Higher order contact of submanifolds of homogeneous spaces[M].New York:Springer-Verlag,1977.
[6]Fels M,Olver P J.Moving coframes.I.a practical algorithm[J]. Acta Appl Math,1998,51:161-213.
[7]Fels M,Olver P J.Moving coframes.II.regularization and theoretical foundations[J].Acta Appl Math,1999,51:127-208.
[8]Olver P J.Joint invariant signatures[J].Found Comput Math,2001(1):3-67.
[9]Kim P,Olver P J.Geometric integration via multi-space[J]. Regular and Chaotic Dynamics,2004,9:213-226.
[10]Calabi E,Olver P J,Shakiban C,et al.Differential and numerically invariant signature curves applied to object recognition[J].Int J Computer Vision,1998,26:107-135.
[11]Olver P J.Classical invariant theory[M].Cambridge:Cambridge University Press,1995.
[12]Kogan I A,Olver P J.Invariant Euler-Lagrange equations and the invariant variational bicomplex[J].Acta Appl Math,2003,76:137-193.
[13]Olver P J.Invariant submanifold flows[J].J Phys A,2008, 41:344-361.
[14]Marí Beffa G,Olver P J.Poisson structures for geometric curve flows on semi-simple homogeneous spaces[J].Regular and Chaotic Dynamics,2010,15:532-550.
[15]Shemyakova E,Mansfield E L.Moving frames for Laplace invariants[C]//Proceedings of ISSAC 2008.New York:ACM,2008:295-302.
[16]McLenaghan R G,Smirnov R G.An extension of the classical theory of algebraic invariants to pseudo-Riemannian geometry and Hamiltonian mechanics[J].J Math Phys,2004,45:1079-1120.
[17]Deeley R J,Horwood J T,McLenaghan R G,et al.Theory of algebraic invariants of vector spaces of killing tensors:methodsforcomputingthefundamentainvariants[J].Proc Inst Math NAS Ukraine,2004,50:1079-1086.
[18]Boyko V,Patera J,Popovych R.Computation of invariants of Lie algebras by means of moving frames[J].J Phys A,2006,39:5749-5762.
[19]Mundy J L,Zisserman A.Geometric invariance in computer vision[M]//Artificial Intelligence.Cambridge:MIT Press,1992.
[20]Weiss I.Geometric invariants and object recognition[J].Acta Applicandae Mathematicae,1993,10:207-231.
[21]Faugeras O.Cartan’s moving frame method and its application to the geometry and evolution of curves in the Euclidean affine and projective planes[M]//Applications of Invariance in Computer Vision.[S.l.]:Springer-Verlag,1994:11-46.
[22]Killing W.Erweiterung der begriffes der invarianten von transformation gruppen[J].Math Ann,1890,35:423-432.
[23]Mansfield E L.A practical guide to the incariant calculus[M]. Cambridge:Cambridge University Press,2010.
[24]Olver P J.Applications of Lie groups to differential equations6[M].2nd ed.New York:Springer-Verlag,1993.
[25]Olver P J.Recursive moving frames[J].Results Math,2011,60:423-452.
[26]Kogan I A.Inductive approach to Cartan moving frame method with applications to classical invariant theory[D].University of Minnesota,2000.
[27]Kogan I A.Inductive construction of moving frames[J].Contemp Math,2001,285:157-170.
[28]Kogan I A.Two algorithms for a moving frame construction[J].Cannad J Math,2003,55:266-291.
CHENG Limei,YUAN Wei,YAO Ruoxia
School of Computer Science,Shaanxi Normal University,Xi’an 710062,China
This paper presents a classical algorithm and an improved recursive method to construct moving frames and differential invariants based on the moving frame theory developed by Peter J.Olver and Mark Fels.It takes an example to demonstrate the constructive processes of two methods respectively for a Lie transformation group.The results indicate that the recursive algorithm has more advantages than the classical Maurer-Cartan approach,which can be applied to arbitrary group actions systematically. More importantly,it does not need the existing of a slice.Especially for multi-parameter transformation group,this recursive method is more convenient while constructing the corresponding moving frames and differential invariants.It is important that the corresponding Maurer-Cartan forms can be obtained as by-products step by step.The results presented here not only are new, but also provide a fundamental theory tool to the application study of signature curve for differential invariants.
recursive algorithm;classical Maurer-Cartan approach;moving frame;differential invariant
基于Mark Fels和Peter J.Olver的活动标架理论,给出了用经典算法和改进的递归算法来构造活动标架和微分不变量的代数构造算法,并以一个李变换群为例演示了两种方法的构造过程。结果证明递归构造方法与经典的Maurer-Cartan方法相比较,不仅能够系统地应用于任意的变换群作用,也不要求一个slice的存在,且对于多参数的变换群来说,其递归构造方式使得相应的活动标架和微分不变量的构造过程更便捷,也容易实现。重要的是,相应的Maurer-Cartan形也被一步步地构造获得。所获得结果不仅是新的,且为微分不变量在签名曲线中的应用研究提供了基础理论支撑。
递归算法;经典Maurer-Cartan算法;活动标架;微分不变量
A
TP301
10.3778/j.issn.1002-8331.1112-0527
CHENG Limei,YUAN Wei,YAO Ruoxia.Constructing moving frames and differential invariants and its applications in pattern recognition.Computer Engineering and Applications,2013,49(19):147-152.
国家自然科学基金面上项目(No.11071278)。
成丽美(1986—),女,硕士研究生,主要研究方向:符号计算;袁伟(1984—),硕士研究生,主要研究方向:符号计算;姚若侠(1968—),通讯作者,女,博士/博士后,教授,研究生导师,主要研究领域:计算复杂性与符号计算,机器证明,孤子理论,可积系统。E-mail:rxyao2@hotmail.com
2012-01-02
2012-03-01
1002-8331(2013)19-0147-06
CNKI出版日期:2012-05-21http://www.cnki.net/kcms/detail/11.2127.TP.20120521.1139.018.html

