基于训练字典的遥感图像融合

刘婷，程建

电子科技大学电子工程学院，成都 611731

基于训练字典的遥感图像融合

刘婷，程建

电子科技大学电子工程学院，成都 611731

1 引言

遥感图像融合的目的就是利用数据间的互补性和冗余性，将多光谱图像和全色图像进行融合，使融合后的图像在保持原始光谱特性的同时尽可能地增加图像的空间细节信息，从而获得目标场景的最大信息描述，这样不但提高了遥感图像的质量，而且更有利于遥感图像的分类和目标识别等后续处理[1-2]。现有的方法，如IHS变换、PCA变换以及小波变换等[3]，都能提高融合后图像的空间分辨率，然而IHS融合方法扭曲了原始的光谱特性，产生了光谱退化现象或彩色畸变；PCA融合方法同样会导致光谱退化；小波变换不能有效捕获图像的任一方向的信息，并且缺乏平移不变性，造成重构图像的尖锐边缘附近的均匀局部区域出现抖动。

稀疏表示是当前非常有效的信号和图像处理工具。稀疏模型也被广泛应用于信号和图像处理等领域，该模型通过基或字典中极少量元素线性组合的形式来描述信号[4-5]。Hu等[6]提出基于稀疏表示和IHS变换的遥感图像融合，这种方法虽然较好地保持了光谱信息，空间细节信息也有所提高，但由于选取的是DCT字典，不能很好地对边界结构信息进行稀疏表示，很难适应结构复杂的遥感图像；而且选择的是稀疏系数绝对值取大的融合规则，没有很好地利用全色图像和亮度分量的局部信息。

针对上述不足，本文利用训练字典具有更好的稀疏性和自适应能力的特性，提出了基于训练字典的融合算法。通过对样本进行学习得到训练字典，对图像进行稀疏表示，对IHS变换后的亮度分量进行亮度平滑滤波（SFIM）[7]，很好地保持了多光谱图像的光谱特性，并在一定程度上有提高空间细节信息的作用，对稀疏系数采用空间频率取大的融合规则，很好地利用了图像间的相关性。实验分别采用IKONOS和Quickbird数据，融合结果的目视效果和客观评价表明，该算法能提高融合后图像的空间细节信息，并且能很好地保留多光谱影像的光谱信息。

2 稀疏表示基本理论

稀疏表示以CS（Compressed Sensing，压缩传感）理论为基础，寻找信号在一组字典下的最稀疏表示。图像的稀疏模型要求将图像表示为一组字典中少数几个典型原子的线性组合，基本思想是假设自然信号能由预定义原子中极少数原子进行线性表示[8]。

稀疏表示问题可以由如下的数学形式进行表示：

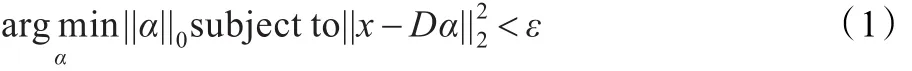
其中，α为x的稀疏表示系数，D={d1，d2，…，dN}∈RM×N(M＜N)为过完备字典，||·||0为l0范数，表示非零元素的个数，ε为逼近误差容限。

当字典D为冗余字典时，求解稀疏表示最优化问题成为一个NP-hard问题，目前常用的方法有：基追踪法（Basis Pursuit，BP）[9]，是将l0范数转换为l1范数进行求解的线性规划问题；匹配追踪（Matching Pursuit，MP）[10]、正交匹配追踪（Orthogonal Matching Pursuit，OMP）[11]及其改进算法。其中，OMP算法克服了BP算法计算复杂度高和MP算法迭代次数多的问题，是目前应用最广泛的稀疏分解方法。本文采用OMP算法进行稀疏分解。OMP算法的核心思想是在每次迭代过程中，选择与当前残留量最相关的原子，然后重新计算残留量，循环上述过程，直到停止条件满足。

3 训练字典

在信号与图像的稀疏分解和稀疏表示中，字典具有决定性的作用。字典的过完备性决定了稀疏分解过程的计算复杂度，也决定了稀疏分解结果稀疏表示的稀疏性，字典中原子的选择也对图像表示的稀疏性有着重要的影响。通常有两种方法构造字典[12-13]：第一种是预先定义字典数学表达式的方法，常用的字典有DCT、小波、曲线波（Curvelets）、轮廓波（Contourlets）等，这些都是预先定义数学表达式的字典，虽然计算复杂度低，但是对图像的几何特征过于依赖，仅仅只对图像的一种或某些特征能有较好的稀疏表示。例如，DCT字典空域局部性差，对边界等结构信息稀疏表示能力差；小波字典对图像的轮廓特征不能有很好的稀疏表示；轮廓波字典虽然能够很好地表示图像的轮廓特征，但缺乏周期性，对纹理图像稀疏表示能力差。另一种是基于学习的方法，它是通过对样本数据进行训练得到的。基于学习的字典能够更准确地从样本数据中提取复杂的图像特征，对图像的各种特征有更好的稀疏表示，具有更好的自适应性。因此，对于拥有复杂特征的遥感图像，本文选取训练字典对其进行稀疏表示。

从选择的样本图像中随机提取K张子图像，构成训练样本集F={fi}Ki=1，目标是从这些样本集中训练得到能够很好地稀疏逼近样本块的字典[14]。假设f∈Rn为训练样本，D={d1，d2，…，dK}为待构造的过完备字典，di为Rn空间的原子，对于训练样本F∈Rn×K，构造目标函数如下：

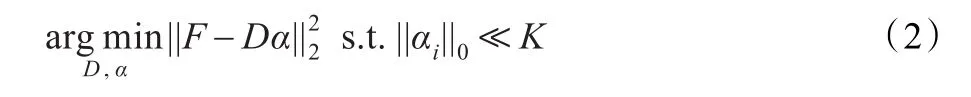
其中，αi为样本fi所对应的稀疏表示系数，每个样本列向量fi对应于一个训练图像块。

4 基于训练字典的遥感图像融合

4.1 SFIM算法

SFIM算法[7]基本思想是去掉高分辨率影像的光谱和地形信息，将剩余的纹理信息直接添加到多光谱影像中。SFIM运算公式如下：

其中，Msi为原始多光谱图像的第i波段，Pan为全色图像，Panmean为全色图像经过均值滤波后图像，Ms(fusion)i为融合后第i个波段图像。SFIM模型能够很好地保持光谱特征，并加人多光谱图像中缺失的空间细节信息。

4.2 空间频率

图像的空间频率是衡量图像空间的整体活跃程度的一个重要指标，反映了图像的边缘化程度，能很好地描述图像的灰度突变信息。定义为：

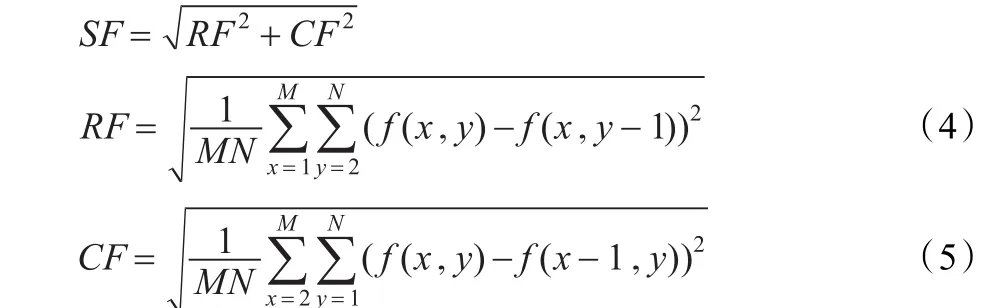
其中，RF为空间行频率，CF为空间列频率，空间频率越大则图像越清晰、越活跃。

4.3 融合算法

Hu等[6]提出基于稀疏表示和IHS变换的遥感图像融合，基本思路是对多光谱图像进行IHS变换后，对I分量和全色图像进行稀疏表示，之后用绝对值取大的融合规则对其稀疏系数进行融合，重构I分量，最后进行IHS逆变换，得到融合图像。这种方法虽然较好地保持了光谱信息，空间细节信息也有所提高。但由于选取的是DCT字典，不能很好地对边界结构信息进行稀疏表示，很难适应结构复杂的遥感图像；而且选择的是稀疏系数绝对值取大的融合规则，没有很好地利用全色图像和I分量的局部信息。

本文选择对遥感图像有更好的稀疏表示能力，并且自适应能力强的训练字典。由于不同的卫星传感器反应不同的光谱特性，因此选取与实验图像有相同传感器的遥感图像作为样本数据，通过随机采样样本图像块来构造训练字典。此外，为了很好地保持光谱特性，并提高空间细节信息，本文将SFIM算法与IHS变换相结合，对与光谱特性不相关的I分量进行SFIM运算，将空间细节信息加入到I分量中，这样能尽可能少地影响光谱信息，并通过SFIM模型能将空间细节信息合理、有效地调制到多光谱图像亮度分量中。然后对进行SFIM运算后的亮度分量和全色图像进行稀疏表示，得到稀疏表示系数。文献[6]选择绝对值取大的融合规则，没有考虑到图像的局部信息，最终融合图像空间细节信息增强也有限。因此本文选择空间频率取大的融合规则，充分利用了图像中像素间局部特征，有效地提高了融合图像的空间细节信息。

假设全色图像与多光谱图像已经配准成功，全色图像的大小为M×N，本文融合算法步骤如下：

（1）将多光谱图像重采样到与全色图像同样大小，对多光谱图像进行IHS变换，分别得到I、H和S分量。

（2）对全色图像Pan选取窗口大小为5×5的均值滤波，然后和I分量执行SFIM得到新的I分量：

其中，Panmean表示对Pan均值滤波后的图像，Inew表示最后得到的新的I分量。

（3）用窗口大小为n×n遍历图像Inew和Pan，将每一个块按列优先方式转换为大小为n2×1的向量，再按照遍历顺序将这些列向量排列为大小为n2×((M-n+1)·(N-n+1))的矩阵，最后分别利用OMP算法以及训练字典计算出稀疏表示系数为AI和APan。

（4）分别计算Inew分量和全色图像每个块的空间频率SFI和SFPan，选择空间频率大的稀疏系数为融合后的稀疏表示系数[15]：

（5）根据IF=DAF从融合的稀疏系数重构出图像块，这时原图像中同一像素位置可能出现在多个块中，将所有块按其原来位置进行放置，然后进行加权平均，从而得到融合的I分量，结合H分量和S分量进行IHS逆变换，得到融合图像。

5 实验结果与分析

针对本文提出的融合算法，进行了两组仿真实验：第一组采用Quickbird卫星的多光谱图像和全色图像为研究对象；第二组采用IKONOS卫星的多光谱图像和全色图像为研究对象。采用的Quickbird数据集包含空间分辨率为2.4 m的多光谱图像和0.6 m的全色图像，IKONOS数据集包含空间分辨率为4 m的多光谱图像和1 m的全色图像。两组图像都经过几何校正、图像配准等预处理步骤，选择图像大小为256×256，进行分块的窗口大小为8×8，SFIM方法使用的卷积核大小为5×5。通过随机采样样本图像块来构造字典，由于不同的卫星传感器反应不同的光谱特性，因此选取与实验图像有相同传感器的遥感图像作为样本数据。从样本图像中随机选取50 000张大小为8×8的图像块，字典大小为64×256，其冗余因子为4。如图1所示为DCT字典，样本数据为Quickbird的训练字典以及样本数据为IKONOS的训练字典。

图1 用于实验的相关字典

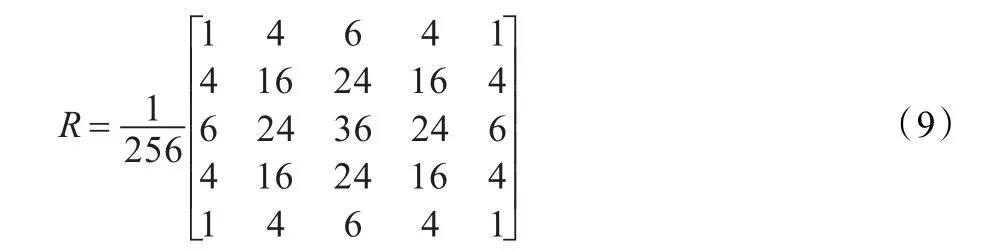
Atrous小波算法[16]就是把图像分解为低频图像和各高频小波面，即

其中，Cn(k)为低频子图像，wj(k)为各高频小波面。Atrous小波算法可以很容易扩展到二维空间。在二维空间其算法类似于用卷积核对影像进行滤波，由于B3对不规则样本数据具有很好的插值型，通常被选择作为尺度函数，其二维卷积核为：

5.1 评价指标

融合图像与多光谱图像的相关系数CC定义如下：

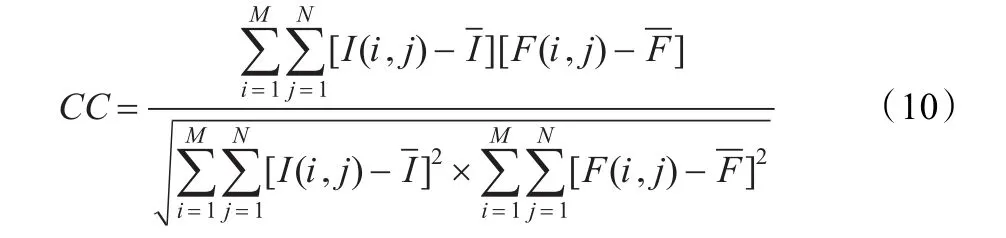
标准差std定义如下：

其中，M、N表示图像的大小，F(i，j)表示图像在(i，j)处的像素值，u为其均值。标准差反映了图像灰度相对于平均亮度的离散情况，标准差越大，则灰度级分布越分散。

平均梯度grad定义如下：

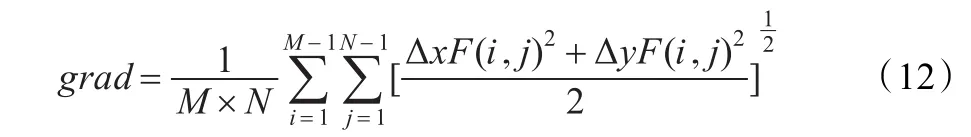
其中，ΔxF(i，j)、ΔyF(i，j)分别为F(i，j)在x、y方向上的一阶差分。平均梯度反映了图像的清晰程度，同时还反映出图像中微小细节反差和纹理变换特征。平均梯度越大，图像层次越多，也越清晰。

图2 逼近误差对Quickbird图像融合质量的影响

结构相似度SSIM定义[17]如下：

SSIM值越大表示两幅图像越相似。

图像峰值信噪比PSNR定义[3]如下：

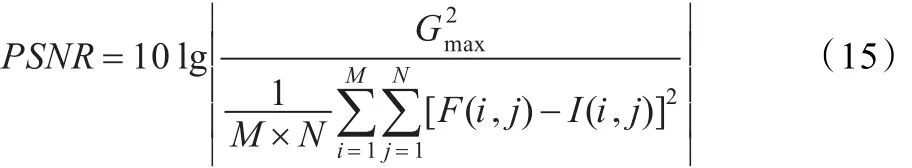
其中，Gmax表示图像中的最大灰度。PSNR值越大，说明噪声越小，图像融合的效果越好。

5.2 实验结果

逼近误差反应了稀疏分解的逼近程度，不同的逼近误差实验的结果也不相同，所需的计算时间也不相同，把不同的逼近误差下对实验结果的影响进行比较，图2和图3为选取不同的逼近误差下，各个指标的折线图。相关系数随着逼近误差的减少逐渐变小，这是由于逼近误差越小，稀疏表示系数的非零元素越多；平均梯度随着逼近误差的减少而增大，最终趋于平滑，是由于非零元素增多后，其表示细节的能力更强，且融合规则选用的是空间频率取大的原则，也能增加图像的细节信息。随着逼近误差的减少，所需运算时间越大。由图2和图3可以看出，Quickbird和IKONOS融合实验中，选取逼近误差均为0.02时，融合效果较好，本文选择逼近误差为0.02做融合实验。同时，对多光谱图像大小为256×256和全色图像大小为1 024×1 024的Quickbird和IKONOS也进行了仿真。本文算法利用Matlab 7编程实现，运行环境Pentium Dual-Core E5300，2.6 GHz CPU，2 GB内存，操作系统Windows XP。

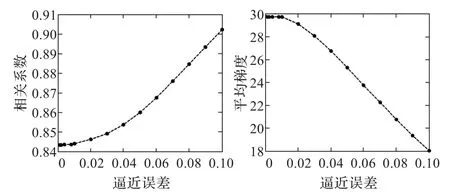
图3 逼近误差对IKONOS图像融合质量的影响

为了验证融合算法的有效性，对来自不同场景、不同卫星的多光谱图像和全色图像进行了融合实验，所用图像都已经经过精确的几何校正、图像配准等预处理技术。

图4给出了Quickbird多光谱图像和全色图像的融合结果，从目视效果可以看出各种融合结果与原始多光谱图像相比较，空间分辨率均有增强，如公路、植被、建筑等空间细节信息有明显的提高。IHS变换在亮度分量的替代过程中丢失了部分原始多光谱特征，虽然融合结果空间细节信息比较清晰，但是光谱失真严重，如植被的颜色明显变浅；atrWT和contourlet融合结果光谱特征失真较小，空间细节信息丰富；本文算法与文献[6]的方法相比，融合图像光谱失真更小，细节信息更丰富，融合效果更好。

表1列出了Quickbird数据下各种融合算法的客观评价指标，可以看出IHS算法的相关系数、结构相似度以及峰值信噪比最小，说明光谱失真最严重，清晰度最小；atrWT算法的梯度和方差最小，说明图像的空间细节信息在一定程度上有较大的损失；contourlet算法和文献[6]的方法有较高的相关系数和结构相似度，但是梯度较小，说明图像的光谱失真较小，但是空间细节信息有一定的损失；本文算法的结构相似度略低于contourlet，其他指标均比contourlet高，说明本文算法和contourlet算法都能很好地保持光谱特征，而且本文算法融合图像的纹理细节信息最丰富，清晰度最好。

表1 Quickbird数据融合结果的客观评价指标

图4 Quickbird图像及融合结果

图5 IKONOS图像及融合结果

图6 全色图像大小为1 024×1 024的Quickbird图像及融合结果

图7 全色图像大小为1 024×1 024的IKONOS图像及融合结果

图5给出了IKONOS多光谱图像和全色图像的融合结果，从目视效果可以看出，本文算法融合结果视觉效果最好，光谱特征保持最好，空间细节信息最丰富，图像最清晰。和atrWT变换、contourlet相比，本文算法融合结果更加清晰，细节特征更加明显；相比IHS变换和文献[6]的方法，本文方法光谱失真最少，视觉效果最好。

表2列出了IKONOS数据下各种融合算法的客观评价指标，可以看出本文算法的平均梯度、方差和峰值信噪比明显高于contourlet，仅结构相似度和相关系数略低于contourlet算法，说明本文算法和contourlet算法都能很好地保持光谱特征，而且本文算法能更好地提高图像细节信息。本文算法与其他三种方法相比，具有最高的相关系数、结构相似度、平均梯度、方差和峰值信噪比，说明融合结果既保留了丰富的光谱信息又提高了空间细节信息。

表2 IKONOS数据融合结果的客观评价指标

表3给出了本文算法和其他四种算法的执行时间，由于在进行稀疏分解时耗时较大，所以本文算法执行时间高于传统算法。虽然执行时间较传统算法高，但本文算法能较好地保持图像的光谱特征，并提高融合结果的清晰度以及空间细节信息，更有利于图像的分类和目标识别等后续处理。

表3 运行时间s

图6和图7分别给出了多光谱图像大小为256×256和全色图像大小为1 024×1 024的Quickbird和IKONOS多光谱图像和全色图像融合结果。表4和表5分别列出了Quickbird和IKONOS数据下各种融合算法的客观评价指标，从目视效果和融合评价指标可以看出，本文算法融合图像最清晰，空间细节信息更丰富，光谱特征保持的最好。

表4 全色图像大小为1 024×1 024的Quickbird数据融合结果的客观评价指标

表5 全色图像大小为1 024×1 024的IKONOS数据融合结果的客观评价指标

6 总结

在遥感图像融合中，很难得到分辨率高，光谱畸变小的融合图像。本文将稀疏表示理论用于遥感图像融合，采用训练字典，有效地利用了训练字典的自适应性，对图像有着更好的稀疏表示；为了提高融合结果的空间细节信息，对IHS变换后的亮度分量进行SFIM运算，能有效地保留多光谱图像的光谱特征并增加空间细节信息；选取的空间频率取大的融合规则也很好地利用了图像的局部信息，与文献[6]中取绝对值大的融合规则相比较，能很有效地增强融合结果的空间细节信息。为了证明算法的有效性，对Quickbird和IKONOS两组不同数据类型进行了实验和分析，结果证明，本文算法比IHS变换、contourlet、atrWT变换以及文献[6]的方法有更好的光谱保持能力和增强空间细节的能力，从而得到了融合质量更高的图像。

[1]Simone G，Farina A，Morabito F C，et al.Image fusion techniques for remote sensing applications[J].Information Fusion，2002，3（1）：3-15.

[2]Pohl C，Genderen J L.Multisensor image fusion in remote sensing：concepts，methods，and applications[J].International Journal of Remote Sensing，1998，19（5）：823-854.

[3]敬忠良，肖刚，李振华.图像融合——理论与应用[M].北京：高等教育出版社，2007：1-262.

[4]石光明，刘丹华，高大化，等.压缩感知理论及其研究进展[J].电子学报，2009，37（5）：1070-1081.

[5]石慧，宋仁旺，王钢飞.OFDM系统稀疏信道估计研究.[J].计算机工程与应用，2011，47（33）：98-100.

[6]Hu Jianwen，Li Shutao，Yang Bin.Remote sensing image fusion based on IHS transform and sparse representation[C]//Proceedings of the 2010 Chinese Conference on Pattern Recognition（CCPR），2010：1-4.

[7]Liu J G.Smoothing filter-based intensity modulation：a spectral preserve image fusion technique for improving spatial details[J]. Int J Remote Sensing，2000，20（18）：3461-3472.

[8]Yang Bing，Li Shutao.Multifocus image fusion and restoration with sparse representation[J].IEEE Transaction on Information Theory Instrumentation and Measurement，2010，59（4）：884-892.

[9]Donoho D，Elad M.Optimally sparse representation in general（non-orthogonal）dictionaries via l1 minimization[J].Proc Nat Aca Sci，2003，100：2197-2202.

[10]Mallat S，Zhang Z.Matching pursuits with time-frequency dictionaries[J].IEEE Transactions on Signal Processing，1993，41（12）：3397-3415.

[11]Pati Y，Rezaiifar R，Krishnaprasad P.Orthogonal matching pursuit：recursive function approximation with applications to wavelet decomposition[C]//Proceedings of the 27th Annual Asilomar Conference on Signals，Systems，1993，1：40-44.

[12]Rubinstein R，Zibulevsky M，Elad M.Double sparsity：learning sparse dictionaries for sparse signal approximation[J].IEEE Transactions on Signal Processing，2009，58（2）：1553-1564.

[13]Yang J，Wright J，Huang T，et al.Image super-resolution via sparserepresentation[J].IEEETransactiononImageProcessing，2010，19（11）：2861-2873.

[14]Wang J，Zhu S，Gong Y.Resolution enhancement based on learning the sparse association of image patches[J].Pattern Recognition Letters，2010，31（1）：1-10.

[15]Li S，Kwok J T，Wang Y.Combination of images with diverse focuses using the spatial frequency[J].Information Fusion，2001，2（3）：169-176.

[16]Chibani Y.Radar and panchromatic image fusion by means of the atrous algorithm[J].SPIE，2004，5238：543-550.

[17]Wang Z，Bovik A C，Sheikh H R，et al.Image quality assessment：from error visibility to structural similarity[J].IEEE Transactions on Image Processing，2004，13（4）：600-612.

LIU Ting,CHENG Jian

School of Electronic Engineering,University of Electronic Science and Technology of China,Chengdu 611731,China

An image fusion algorithm is presented based on sparse representation and training dictionary in order to improve the fusion quality of multi-spectral image and panchromatic image.A new intensity component is firstly obtained by taking the method of smoothing filter-based intensity modulation on the original intensity component of the multi-spectral image.The panchromatic image and intensity component are obtained for their sparse coefficient through training dictionary which generated by randomly sampling raw patches.Then,the fused coefficient is obtained by the fusion rule which choosing spatial frequency maximum. Finally,the fused results are obtained through reconstruction and IHS inverse transformation.The improved algorithm has been tested on various multi-spectral and panchromatic satellite remote sensing images for different areas.The experimental results prove that the proposed method can improve the spatial resolution and better maintain the spectral characteristics.

image processing;image fusion;sparse representation;training dictionary

为了提高多光谱图像与全色图像的融合质量，利用稀疏表示理论，提出了一种基于训练字典的融合算法。该算法对多光谱图像的亮度分量进行亮度平滑滤波（SFIM）得到新的亮度分量，利用图像块随机采样学习得到的训练字典对全色图像和新的亮度分量进行稀疏表示，采用空间频率取大的融合规则对稀疏系数进行融合，通过重构和IHS逆变换得到融合结果。对不同场景、不同卫星的多光谱图像和全色图像进行实验，结果表明，该方法能在提高空间分辨率的同时更好地保持光谱特性。

图像处理；图像融合；稀疏表示；训练字典

A

TP751

10.3778/j.issn.1002-8331.1112-0650

LIU Ting,CHENG Jian.Remote sensing image fusion based on training dictionary.Computer Engineering and Applications,2013,49（19）：135-140.

教育部高等学校博士学科点专项科研基金（No.20100185120021）；国家重点基础研究发展计划（973）（No.2007CB714406）；电子科技大学中央高校基本科研业务费项目（No.ZYGX2009Z005）；电子科技大学青年科技基金重点项目（No.JX0804）。

刘婷（1989—），女，硕士，主要研究领域为遥感图像处理，稀疏表示；程建（1978—），男，博士后，副教授。E-mail：liutinglady@163.com

2012-01-06

2012-04-13

1002-8331（2013）19-0135-06

CNKI出版日期：2012-05-28http://www.cnki.net/kcms/detail/11.2127.TP.20120528.1612.002.html