二次整数环上的ElGamal密码体制和签名方案

董学东，张妍

1.大连大学信息工程学院，辽宁大连 116622

2.辽宁师范大学数学学院，辽宁大连 116029

二次整数环上的ElGamal密码体制和签名方案

董学东1，张妍2

1.大连大学信息工程学院，辽宁大连 116622

2.辽宁师范大学数学学院，辽宁大连 116029

1 引言

ElGamal公钥密码体制和签名方案是1985提出的[1]，ElGamal签名方案的变型被美国国家标准技术研究所采纳为数字签名算法（Digital Signature Al，DSA），它的安全性主要基于有限域上离散对数问题的难解性。文献[2]提出了有限域上多项式形式的ElGamal体制。文献[3]提出了基于四元整数环的RSA公钥密码方案。受到这些启发，本文利用文献[4]的一个结果提出了二次数域的代数整数环上的ElGamal公钥密码体制和ElGamal签名方案，其安全性基于代数整数环上离散对数问题的难解性。

2 预备知识

设m是没有平方因子的整数并且m≠1，又设

3 ElGamal公钥密码体制

3.1 密钥生成的过程

3.2 加密过程

假设用户A发送消息给用户B，用户A获取用户B的公钥(α，γ)，将明文消息ω写成a+bδm，0≤a，b＜pn，用户A随机地选取k，计算c1=αk(modpn)，c2=γkω(modpn)，于是得到密文(c1，c2)，将其发送给用户B。

3.3 解密过程

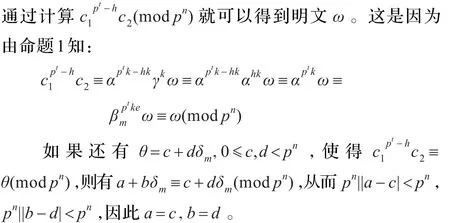
3.4 安全性分析

3.5 实例

就可以得到明文ω。

4 ElGamal签名方案

4.1 系统初始化

设H是一个安全的单向Hash函数，其函数值属于正整数集合。

4.2 签名过程

假设用户A想对一个消息ω签名，首先计算消息ω离散值u=H(ω)其次，选取一个秘密的随机数k，(k，p)=1，计算ζ≡αk(modpn)，s≡k-1(u-h)(modpn-1)，这里k-1是指k模pn-1的逆，签署的消息是三元组(ω，s，ζ)。

4.3 验证过程

4.4 安全性分析

假定系统攻击者想对消息伪造签名，他就必须获得秘密数h≡ks-u(modpn-1)。系统攻击者选择一个值u和ζ≡αk(modpn)，然后试图从关系式αu≡γζs(modpn)中找到相应的s进而计算秘密数h≡ks-u(modpn-1)，那么他必须计算离散对数logζγ-1αu，而这是公认的数学难题。需要说明的是，在计算签名时所使用的随机值k不能泄露。如果泄露出去，那么计算h≡ks-u(modpn-1)就是容易的事。一旦h被泄露，系统攻击者就能随意地伪造签名了。对于两个不同的消息签名要使用不同的k值，如果在两个不同的消息签名中使用同一个k，则有s1≡k-1(u1-h)(modpn-1)，s2≡k-1(u2-h)(modpn-1)，于是以k为未知量的同余方程k(s1-s2)≡u1-u2(modpn-1)有(s1-s2，pn-1)个解。这(s1-s2，pn-1)个解就是秘密的随机数k的候选值。从等式ζ≡αk(modpn)检测出唯一正确的那一个k，再从h≡(ks1-u1)≡(ks2-u2)(modpn-1)就得到了密钥h，他就可以在任何文档上伪造签名了。

5 结束语

本文提出了二次数域的代数整数环上的ElGamal公钥密码体制和ElGamal签名方案。加密、解密的计算过程相对简单，其安全性基于离散对数问题的难解性。

[1]ElGamal T.A public key cryptosystem and a signature scheme based on discrete logarithms[J].IEEE Transactions on Information Theory，1985，31：469-472.

[2]张青坡，陈彩云，陈鲁生，等.有限域上多项式形式的ElGamal体制及数字签名方案[J].通信学报，2005，26（5）：69-72.

[3]汪丽，邢伟，徐光忠.基于四元整数的ElGamal公钥密码体制[J].计算机应用，2008，28（5）：1156-1157.

[4]Dong X，Cheong B，Erry G，et al.Groups of algebraic integers used for coding QAM signals[J].IEEE Transactions on Information Theory，1998，44（5）：1848-1860.

DONG Xuedong1,ZHANG Yan2

1.College of Information Engineering,Dalian University,Dalian,Liaoning 116622,China
2.School of Mathmatics,Liaoning Normal University,Dalian,Liaoning 116029,China

A new ElGamal public key cryptosystem and digital signature scheme are presented over algebraic integral rings of quadratic number fields.Their securities depend on difficulty of discrete logarithmic computations in the algebraic integral rings.

ElGamal Public Key Cryptosystem（PKC）;digital signature scheme;algebraic integral ring

提出了二次数域的代数整数环上的ElGamal公钥密码体制和ElGamal签名方案，其安全性基于离散对数问题的困难性。

ElGamal公钥密码；签名方案；代数整数环

A

TP309.7

10.3778/j.issn.1002-8331.1201-0031

DONG Xuedong,ZHANG Yan.ElGamal cryptosystem and digital signature scheme over integral rings of quadratic number fields.Computer Engineering and Applications,2013,49（19）：73-74.

国家自然科学基金（No.10171042）；辽宁省教育厅高校科研项目（No.L2010234）。

董学东（1961—），男，博士，教授，主要研究领域为编码密码学；张妍（1978—），女，博士研究生，讲师。E-mail：dongxu-edong@dl.cn

2012-01-04

2012-03-01

1002-8331（2013）19-0073-02

CNKI出版日期：2012-06-01http://www.cnki.net/kcms/detail/11.2127.TP.20120601.1458.053.html