多目标优化非支配集构造方法的研究进展

李志强，蔺想红

西北师范大学计算机科学与工程学院，兰州 730070

多目标优化非支配集构造方法的研究进展

李志强，蔺想红

西北师范大学计算机科学与工程学院，兰州 730070

1 引言

最优化问题是工程实践和科学研究中主要的问题形式之一，其中目标函数超过一个并且需要同时处理的最优化问题被称为多目标优化问题[1-2]（MOP）。通常情况下，同一问题中的多个目标函数相互制约，是彼此矛盾的，因此最终结果是获得一系列折衷解的集合，称为Pareto最优解集（Pareto Optimal Set）或非支配解集（Non-dominated Set）。

多目标进化算法（Multi-Objective Evolutionary Algorithm，MOEA）是一类模拟生物进化机制而形成的全局性概率优化搜索方法，特别适合用于解决多目标优化问题，已被成功应用于多目标优化领域。近年来，MOEA的研究进入了快速发展阶段，越来越多的研究者开始致力于MOEA的设计与实现，因此MOEA的应用也日益广泛。大多数研究者都着眼于用MOEA解决实际问题，而关于MOEA理论方面的研究成果比较少，例如非支配解集的构造方法、算法的性能评价准则、MOEA的测试以及测试问题的构造等方面。

纵观国内外该领域的研究情况，认为有必要对基于Pareto非支配集构造方法的研究现状作一个全面的介绍。本文首先介绍了多目标优化问题以及用于解决MOP的一般框架，然后描述了目前主要用于构造非支配集几种方法的基本思路，并分析了各自的效率，最后总结和展望了多目标优化非支配集构造方法研究的未来发展趋势。

2 多目标优化问题的数学描述

MOP的解并不局限于单个解，而可能有多个解，求解MOP就是求其Pareto最优解集。不失一般性，一个具有n维决策向量，m维子目标的多目标优化问题描述如下：

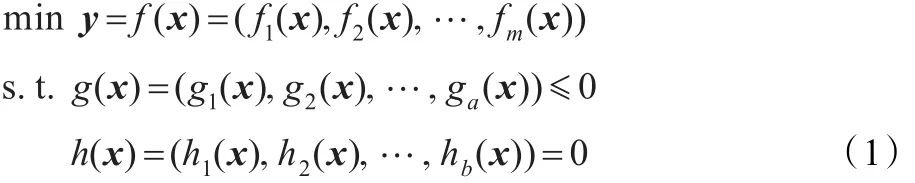
其中，x=(x1，x2，…，xn)∈X，y=(y1，y2，…，ym)∈Y。x表示n维的决策向量，X表示n维的决策空间，y表示m维的目标向量，Y表示m维的目标空间。目标函数f(x)定义了m个由决策向量空间向目标空间的映射函数，该问题具有a个不等式约束和b个等式约束，确定了决策变量可行的取值范围。关于Pareto的一些基本概念如下：

3 多目标进化算法的一般框架

由于MOEA种类较多，所采用的方法和技术有较大差异，本文主要是基于Pareto的多目标进化算法。这类算法解决MOP的一般框架，如图1所示：MOEA从一组随机产生的初始种群P出发，通过对种群执行选择、交叉和变异等进化操作，生成后代群体Q，根据定义1选择P和Q中的非支配个体组合成非支配群体R，然后按照某种策略对非支配集R进行调整，一方面使R满足大小要求，同时也尽量使保留在R的非支配个体具有好的分布性，之后判断是否满足终止条件，若满足终止条件，则结束，否则将R中的个体复制到P中并继续下一趟进化。保留上一代非支配集，并使之参与新一代的进化操作，从而使新一代的非支配集不比上一代差。这样经过多代进化，种群中个体的适应度不断提高，从而进化群体的非支配集逐步逼近真正的最优前沿。

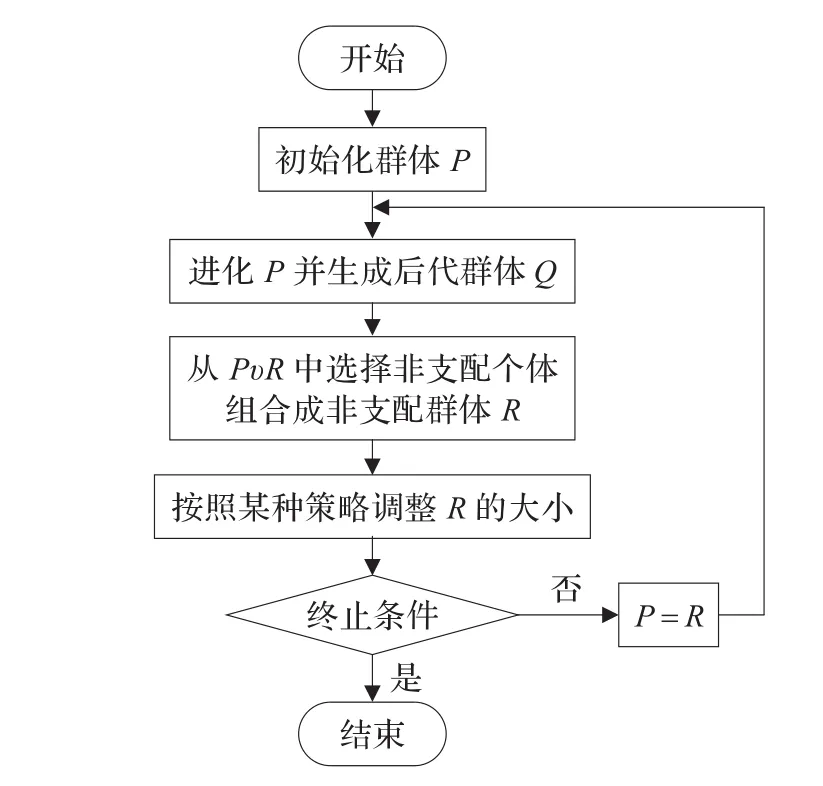
图1 多目标进化算法的基本框架图

MOEA中的每个个体对应一个解，非支配解也称为非支配个体，支配解也称为支配个体。非支配解通常不止一个，构成了一个非支配集，又称为归档集。

MOEA的一个重要步骤就是构造进化群体的非支配解集，并使非支配集不断地逼近Pareto前沿的过程。每一代中非支配个体的集合称为进化群体的非支配集，实际上就是当前进化群体的最优个体集合。因此，如何研究构造一个多目标进化Pareto非支配集，实际上就是研究如何构造进化群体的非支配集。然而，进化算法的每一代进化，都要构造一次非支配集，因而构造非支配集的效率将直接影响多目标进化算法的运行效率。由此可见，高效的非支配解集构造方法是MOEA研究的重要内容。

4 非支配集的主要构造方法

关于多目标进化Pareto非支配集的构造方法，国内外研究人员做了许多工作，下面就详细地概括当前非支配集的构造方法研究的基本现状。

（1）等级排序法

Deb等[3]提出了NSGA-II算法，它是迄今为止最优秀的进化多目标优化算法之一。其构造非支配集的方法是首先根据个体之间的支配关系计算组合种群中每个个体的等级值，然后再计算每个个体的拥挤距离，最后根据个体的等级值和拥挤距离构造新群体。

文献[4]又提出了全方位非支配等级排序的方法，首先对组合种群进行等级排序，然后对各等级中的个体按照其支配关系分别构造各个等级的非支配集。

Rio等[5]基于新的等级策略提出了改进的NSGA-II算法，其思路是依次对每个目标进行排序，并按目标分别记录每个个体的位置，然后按照所有目标个体的位置总和对个体等级赋值。这样具有相同位置的个体其等级是一样，以此进行构造非支配集，算法的效率得到了提高。

（2）递归法

基于分治技术，Kung等[6]采用递归的思想，提出了从向量集合中寻找一组最大向量集的方法：按第一个目标值的大小进行排序，在此基础上不断地进行递归调用。

Jensen[7]扩展了Kung的分治向量排序算法，提出了一种构造非支配集的算法，首先对群体进化预排序，通过递归调用的方法构造非支配集，降低了时间复杂度。但是当目标数目M很大时，算法的效率不断地降低，而复杂度却不断地增加。

Fang等[8]根据分治算法的思想，通过引入支配树这种新的数据结构，用于记录所有群体比较的支配信息，从而减少了非支配个体之间的比较次数，提高了算法效率。

（3）快速排序法

文献[9-10]通过快速排序建立索引表的方式，提出了一种总体优前劣后检查方法，它不直接求原集合的非支配集而是转化成求一个整型集合的非支配集；它制定一个总体上非支配个体在前、支配个体在后的检查序列，并以尽可能少的比较次数检查一个个体的非支配性，一旦发现后面的个体全是支配的，则终止搜索。当非支配集较大时，该算法具有较高的效率。

Zheng等[11]基于快速排序的思想构造进化群体的非支配集，每次选取一个或两个个体作为比较对象，将构造集以比较对象为中心分成两部分：一部分是比较对象支配的个体，这些个体不再进入以后的比较；第二部分是支配比较对象的个体或者是相互不被支配的，若没有个体支配比较对象，则比较对象是非支配个体从而加入到非支配集中。如此，再将第二部分中的个体看做构造集重复以上过程，直到构造集为空时结束。此方法当群体中非支配个体比较多时，到了排序后期有可能形成慢速现象。

Du等[12]通过对每个目标值的大小进行快速排序，然后根据目标值分别记录每个个体的得分值，进而求出所有个体的总得分值，再按总得分值排序得到新的求和序列，最后根据求和序列找出其中的非支配个体，并删除支配个体，从而构造非支配集。此方法采用得分和求和序列的提高技术来减少计算复杂度。

Mishra等[13]也是基于类似的思想构造非支配集的。首先根据第一个目标值的大小进行快速排序得到一排序列表，然后将排序列表中的每个个体与非支配集的个体比较，如果此个体被非支配集中的任一个体支配，将此个体从排序列表中删除；如果非支配集中的个体被此个体支配，则删除非支配集中的个体；如果非支配集中没有个体支配此个体，则把此个体加入到非支配集中。

（4）排除法

排除法[14]的思路是：将进化群体中的每个个体依次与非支配集中的个体比较，如果群体中的个体支配非支配集的个体，将非支配集中的个体删除（即排除掉），如果群体中的个体不被非支配集中任何一个个体所支配，则群体中的个体加入到非支配集中。此方法，非支配集中的个体不一定是非支配的。

（5）庄家法

庄家法[15]的思路是：从构造集中任选一个个体出任庄家，由庄家对其他个体进行支配比较，并将庄家所支配的个体淘汰出局，如果庄家个体不被任何其他个体所支配，则庄家个体即为非支配个体，否则庄家个体在该趟比较结束时也被淘汰出局。按照这种方法进行下一趟比较，直至构造集为空，每一趟比较不一定能构造出一个新的非支配个体。

（6）擂台赛法

擂台赛法[16]的思想是：从构造集中任选一个个体出任擂主，由擂主与其他个体进行支配比较，败者被淘汰出局，胜者成为新擂主，并继续与剩下的其他个体进行比较，最后的擂主即为非支配个体。按照这种方法继续找出其他非支配个体，直至构造集为空。每一趟比较能构造出一个新的非支配个体，此方法具有比较高的构造非支配集的效率。

（7）选举法

用选举法[17]构造非支配集的思路是：从构造集中选出两个个体担任候选竞选个体，保证两个候选竞选个体互不支配，再依次从构造集中选取一个个体与两个候选竞选个体进行比较，败者被淘汰出局，胜者成为新的候选竞选个体。若竞选个体发生替换，则还要再次比较这两个候选竞选个体，淘汰弱者，以保证它们互不支配，并继续该趟比较，一趟比较后，两个候选竞选个体即为非支配个体。按照此方法进行下一趟比较，直至构造集为空。此算法在构造非支配集上有较高的效率。

（8）归一化法

归一化法[18]是基于归一化的思想的，首先计算进化群体中每个个体多目标值的归一化和，按照个体间的支配关系建立进化群体中所有个体从大到小的全排序。排序队列的第一个个体是非支配个体，直接进入非支配集，排序队列中的其他个体依次与非支配集中的非支配个体比较，不被支配的个体就进入非支配集。每一代进化群体中的个体只需要与非支配集中的非支配个体比较，从而减少了比较次数。

（9）伪二叉树法

伪二叉树法[19]是根据个体间的支配关系，从进化群体中选出一个个体，将该个体与当前非支配集中的个体进行比较，淘汰被支配的个体，而未被淘汰的个体将插入到非支配集中第一个被淘汰个体的位置。依次进行，直到进化群体中的个体比较完毕，从而生成排序的伪二叉树。当目标数较大时(M≥5)，构造非支配集的效率比较高。

（10）爬山法和演绎法

最近McClymont等[20]提出了爬山排序和演绎排序法，用于非支配集的构造。爬山法是根据支配个体寻找非支配的个体的过程，首先从一个个体出发，当遇到支配个体时，标记并丢弃此支配个体，接着比较剩余的没有被标记的个体，当遇到非支配个体时，把非支配个体插入到当前前沿中，然后爬山排序移动到其不相关的个体，重复以上过程直到所有个体都被分配赋值。

演绎排序法实现了推理支配，不同于爬山排序法。首先对群体中的个体编号，从第一个个体开始依次作为比较对象，与所有以下的个体进行比较（不比较先前个体），标记被比较对象支配的个体，这些个体以后不再考虑，若有个体支配比较对象，标记比较对象并选择下一个体为比较对象，直至最后一个编号的个体。

目前，国内外研究人员所提出的几类非支配解集的构造方法，其时间复杂度也都不同。而MOEA在每一次迭代时都要构造Pareto非支配集，因此构造Pareto非支配集的效率对MOEA的运行效率有很大的影响。表1给出了以上所有构造非支配集方法的时间复杂度。

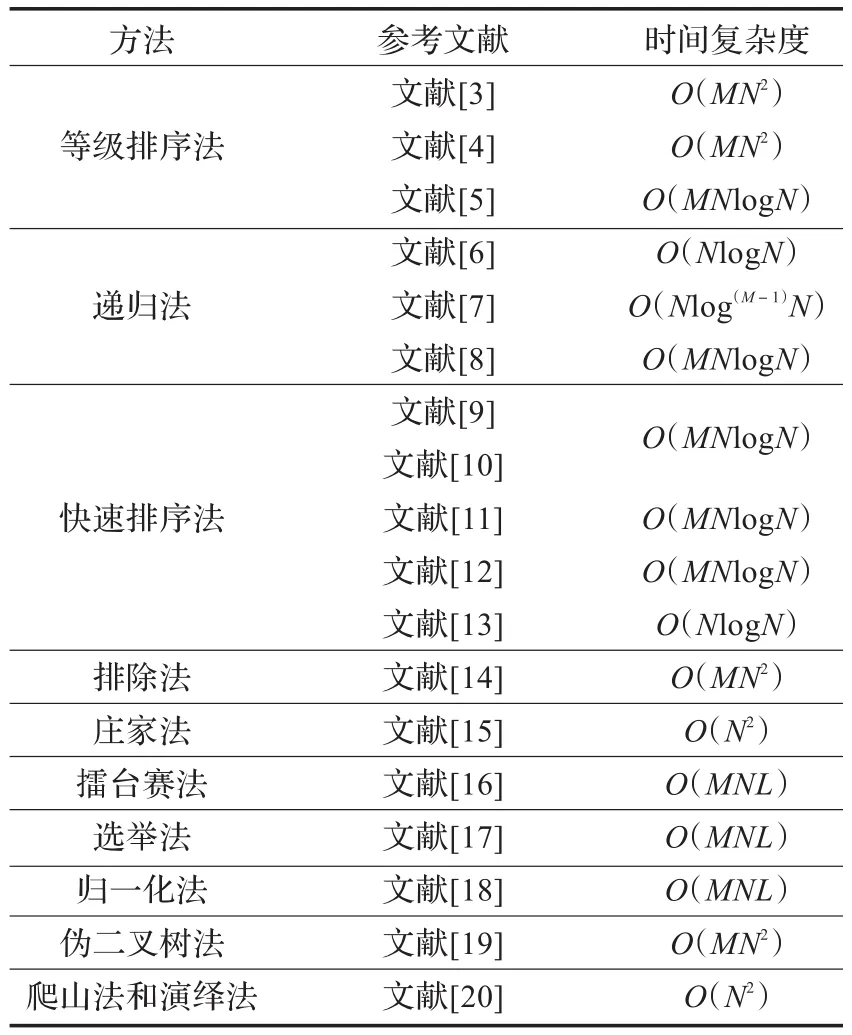
表1 各种构造方法的时间复杂度

表中，M表示目标函数的数目，N表示种群中个体的数目，L为非支配个体的数目。从以上构造多目标Pareto非支配集的方法可以看出，其特点是：非支配解的产生是通过构造集中个体的依次比较来实现的，大多数算法都是尽可能地减少个体之间的比较次数，以提高非支配集的构造效率；多数算法每一趟的比较最多只能找到一个非支配解。

5 结论和展望

多目标进化算法特别适合用于解决多目标优化问题，能同时处理一组可能的解，并在一次算法过程中就可以找到Pareto最优解集中的多个解。目前，多目标进化算法的研究在国内外发展很快，并取得了许多研究成果，也得到了不少研究者的关注，但是多目标进化算法理论及其应用还值得更加深入地研究和完善。近年来，也有一些研究者致力于构造多目标Pareto非支配集，这就非常有必要从理论上论证，对于一个有M个目标的优化问题，构造Pareto非支配集最小的计算复杂度，其中主要的时间开销在于非支配集的构造上，因此一个快速的构造非支配集的算法有利于提高MOEA的效率。

对于一个多目标优化问题，一般的思路是先通过各种进化算法构造非支配集，并使其扩散到整个Pareto前沿。虽然MOEA已经受到越来越多的关注，但在MOEA的发展和应用过程中，仍有大量问题值得研究和探索。进一步可能的研究方向包括：

（1）构造效率。多目标Pareto非支配解集的构造效率是一个值得关注的问题，特别是应用到解决实际问题的时候。提高效率的方式主要有两种：一种是改进现有的构造方法；而另外一种方式是优化现有的构造方法，合理地设计算法的数据结构来提高运行效率[21-22]。在实际应用方面，第二种方式就非常值得重视。

（2）多策略结合的优势。对于多目标Pareto非支配集构造而言，当非支配集的大小超过了约定值时，可以采用聚类方法[23]来降低非支配集的大小，用于维持群体的多样性。另外，文献[24]结合人工免疫系统模拟免疫学功能、原理和模型，用于构造非支配集，当问题的目标数比较多时，其效率比较高。现有的大多数构造方法都集中在非支配集的搜索，很少考虑到决策者的偏好，结合特定的偏好信息[25-27]能有效地缩小搜索空间。因此，如何将决策者的偏好信息结合到构造非支配集方法中，使所得的结果主要集中在决策者所感兴趣的区域，也是非常值得研究的内容。

[1]Deb M.Multi-objective optimization using evolutionary algorithms[M].Chichester，UM：John Wiley&Sons，2001.

[2]郑金华.多目标进化算法及其应用[M].北京：科学出版社，2007.

[3]Deb K，Pratap A，Agarwal S，et al.A fast elitist multi-objective genetic algorithm：NSGA-II[J].IEEE Transactions on Evolutionary Computation，2002，6（2）：182-197.

[4]Deb K，Tiwari S.Omni-optimizer：a procedure for single and multi-objective optimization[M]//Coello Coello C A，Hernandez A A，Zitzler E.Evolutionary Multi-Criterion Optimization.[S.l.]：Springer，2003：47-61.

[5]Rio G L，Dsouza K，Chandra S，et al.Improved NSGA-II based on a novel ranking scheme[J].Journal of Computing，2010，2：91-95.

[6]Kung H T，Luccio F，Preparata F P.On finding the maxima of a set of vectors[J].Journal of the ACM，1975，22：469-476.

[7]Jensen M T.Reducing the run-time complexity of multi-objective EAs：the NSGA-II and other algorithms[J].IEEE Transactions on Evolutionary Computation，2003，7（5）：503-515.

[8]Fang H，Wang Q，Tu Y C，et al.An efficient non-dominated sortingmethodforevolutionaryalgorithms[J].Evolutionary Computation，2008，16（3）：355-384.

[9]Ding L，Zeng S，Kang L.A fast algorithm on finding the nondominated set in multi-objective optimization[C]//Proceedings of International Conference on Evolutionary Computation，2003.

[10]曾三友，李辉，丁立新，等.基于排序的非劣集合快速求解算法[J].计算机研究与发展，2004，41（9）：1565-1571.

[11]Zheng J，Ling C，Shi Z，et al.A multi-objective genetic algorithm based on quick sort[C]//Proceedings of 17th Conference of the Canadian Society for Computational Studies of Intelligence，Canadian AI，2004，3060：175-186.

[12]Du J，Cai Z，Chen Y.A sorting based algorithm for finding non-dominated set in multi-objective optimization[C]//Proceedings of the 3rd International Conference on Natural Computation（ICNC2007），2007，4：436-440.

[13]Mishra K K，Harit S.A fast algorithm for finding the non dominated set in multi objective optimization[J].International Journal of Computer Applications，2010，25（1）：35-39.

[14]李丽荣，郑金华.基于Pareto Front的多目标遗传算法[J].湘潭大学自然科学学报，2004，26（1）：39-41.

[15]Zheng J，Shi Z，Ling C，et al.A new method to construct the non-dominated set in multi-objective genetic algorithms[C]// Proceedings of the International Conference on Intelligent Information Processing（IIP2004），Beijing China，2004.

[16]郑金华，蒋浩，邝达，等.用擂台赛法则构造多目标Pareto最优解集的方法[J].软件学报，2007，18（6）：1287-1297.

[17]杨平，郑金华，李密青，等.一种快速构造多目标Pareto非支配集的方法：选举法则[J].计算机应用研究，2009，26（2）：488-491.

[18]鲍培明，朱庆保.用于多目标进化的归一化排序非支配集构造方法[J].电子学报，2009，37（9）：23-28.

[19]胡焕耀，董渭清.用伪二叉树法则构造多目标Pareto最优解集的方法[J].西安交通大学学报，2009，43（2）：29-32.

[20]McClymont K，Keedwell E.Deductive sort and climbing sort：new methods for non-dominated sorting[J].Evolutionary Computation，2012，20（1）：1-26.

[21]Mostaghim S，Teich J.Quad-trees：a data structure for storing Pareto-sets in multi-objective evolutionary algorithms with elitism[M]//EvolutionaryComputationBasedMulti-criteria Optimization：Theoretical Advances and Applications.[S.l.]：Springer，2005：81-104.

[22]Shi C，Yan Z，Lu K.A dominance tree and its application in evolutionary multi-objective optimization[J].International Journal of Information Sciences，2009，179（20）：3540-3560.

[23]Zitzler E，Thiele L.Multiobjective evolutionary algorithms：a comparative case study and the strength Pareto approach[J]. IEEE Trans on Evolutionary Computation，1999，3（4）：257-271.

[24]Zhou X，Shen J，Shen J.An immune recognition based algorithm for finding non-dominated set in multi-objective optimization[C]//Proceedings of the IEEE Pacific-Asia Workshop on Computational Intelligence and Industrial Application，2008，1：305-310.

[25]Coello Coello C A.Handling preferences in evolutionary multiobjective optimization：a survey[C]//Proceedings of the Congress on Evolutionary Computation，New Jersey，2000：30-37.

[26]Thiele L，Miettinen K，Korhonen P J，et al.A preference-based evolutionaryalgorithmformultiobjectiveoptimization[J]. Evolutionary Computation，2009，17（3）：411-436.

[27]Sindhya K，Ruiz A B，Miettinen K.A preference based interactive evolutionary algorithm for multi-objective optimization：PIE[C]//Proceedingsofthe6thInternationalConference on Evolutionary Multi-Criterion Optimization（EMO2011），2011，6576：212-225.

LI Zhiqiang,LIN Xianghong

School of Computer Science and Engineering,Northwest Normal University,Lanzhou 730070,China

Constructing the multi-objective optimization non-dominated set is an important step in the Multi-Objective Evolutionary Algorithm（MOEA）.It aims to study the operational efficiency to solve Multi-objective Optimization Problem（MOP）by MOEA.Firstly,the MOP is described as well as the basic framework of solving algorithm is given.Next,several non-dominated set building methods based on Pareto are discussed including their computational complexity.Finally,the future trends of this research filed are concluded and prospected.

Multi-Objective Evolutionary Algorithm（MOEA）;Multi-objective Optimization Problem（MOP）;non-dominated set;Pareto front

多目标优化非支配集的构造是多目标进化算法研究领域的一个重要步骤，旨在研究用多目标进化算法解决多目标优化问题的效率。对多目标优化问题进行了描述并且给出了求解算法的一般框架，结合研究现状讨论了目前该领域几种主要的基于Pareto非支配集的构造算法，以及它们的计算时间复杂度；总结并展望了该领域未来的发展趋势。

多目标进化算法（MOEA）；多目标优化问题（MOP）；非支配集；Pareto前沿

A

TP18

10.3778/j.issn.1002-8331.1305-0004

LI Zhiqiang,LIN Xianghong.Research advance of multi-objective optimization non-dominated set construction methods. Computer Engineering and Applications,2013,49（19）：31-35.

国家自然科学基金（No.61165002）；甘肃省自然科学基金（No.1010RJZA019）。

李志强（1987—），男，硕士研究生，研究领域为神经信息学，进化计算；蔺想红（1976—），男，博士，副教授，研究领域为神经网络,进化计算与人工生命。E-mail：lzq115@163.com

2013-05-07

2013-07-01

1002-8331（2013）19-0031-05