基于激光跟踪仪的Delta并联机构运动学误差标定
张文昌,梅江平,刘 艺,张 新
(天津大学机构理论与装备设计教育部重点实验室,天津 300072)
同串联机构相比,并联机构末端由多条支链同基座相连,具有负载能力强,速度快,重复性好等优势.然而,自由度过约束、被动铰链较多使得其精度较难保证,研究表明制造和装配引起的几何误差是造成并联机构末端位姿误差的重要原因[1],精度标定是改善并联机构几何精度的有效手段,并联机构的标定方法可以分为自标定法[2-4]和外部标定法[5-12]两类.自标定法利用内部传感器或施压外约束获得测量信息,Chiu等[2]利用安装在静平台和动平台之间的可伸缩杆实现了对Hexapod并联机床的标定;邵珠峰等[3]借助静平台上的标准定位圆孔,通过仪器对拉线式编码器进行标定,进而利用线尺在线测量、记录机构中的实际位姿,结合数控系统中的理论轨迹,实现了 3-RRR并联机构的参数辨识;常鹏等[4]针对平面三自由度冗余驱动并联机床提出了基于最小线性组理论的分步自标定方法,可以屏蔽掉不影响终端精度的无关参数.自标定方法的不足在于有些机构的被动铰链安装传感器较为困难甚至不可能(如球铰链).外部标定法利用外部传感器检测末端位姿信息,并构造它们与模型计算值之间的残差,进而通过相应的逆解或者正解辨识模型来识别几何参数.Besnard和 Soons等[5-6]分别探讨了检测末端位姿误差子集以识别几何参数的可行性;黄田等[7-8]提出一种基于最小误差子集检测信息的精度标定方法,并通过仿真验证了方法的有效性;常鹏等[9]认为并联机构末端精度是由一组最少参数线性组合决定的,并提出4个定理进行最少参数线性组合的辨识行分析;刘大炜等[10]对一类特殊三自由度并联机构进行了精度分析,得到机构各误差源对末端精度的影响因子,并结合零部件的加工工艺确定需要标定的误差源,他们的研究为并联机构的标定奠定了理论基础.Rauf等[11]通过使用一套包括双周倾角传感器、线性可变差动变压换能器以及旋转传感器的设备为测量手段对六自由度的 HexaSlide机构进行了标定研究,使其精度得到了大幅度提高,但鲁棒性相对较差.Alberto等[12]以计算机视觉为测量手段对并联机构的标定进行了研究,经济性更强,但这类方法受视觉系统测量精度的限制.
笔者以Delta并联机构为研究对象,在前人工作的基础上,对影响末端精度的几何误差源进行了分析和研究,建立了Delta并联机构的运动学误差模型,进而以激光跟踪仪为测量工具,提出一种步进迭代的误差参数识别方法,并通过实验证明所提方法的有效性.
1 机构运动学误差模型
如图 1所示,Delta并联机构由静、动平台和 3条对称分布的支链组成.各支链中,主动臂与静平台经转动铰连接,从动臂为2条等长的从动杆组成的平行四边形结构,两端分别与主动臂及动平台由球铰连接.3个主动臂在伺服电机驱动下可独立转动,进而使动平台实现三维平动.

图1 Delta并联机构Fig.1 Delta parallel robot
Delta并联机构模型如图 2所示,Ci和 Di分别为从动臂与主动臂及从动臂与动平台连接的球铰中心连线中点,EiFi为从动臂的一条从动杆.系Oxyz为Delta机器人坐标系,原点O位于机器人设计工作空间中心,控制动平台分别沿x、y轴运动,系Oxyz的x、y轴分别与其重合,z轴满足右手定则.为了便于建立机构误差模型,建立支链参考坐标系 Bixiyizi,xi与链中主动臂理想回转轴轴线重合,原点 Bi为 Ci到xi轴的交点,yi轴在△B1B2B3内.动平台中心点P在Oxyz下的度量记为r,表示为
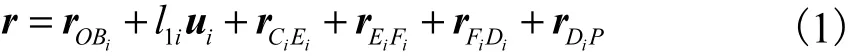
式中:rOBi
为 Bi点在系Oxyz下的位置矢量;l1i为机械手主动臂的长度;ui为主动臂单位方向矢量;rCiEi为Ci到 Ei的位置矢量;为 Ei到 Fi的位置矢量;rFiDi为 Fi到 Di的位置矢量;rDiP为 Di到P的位置矢量.
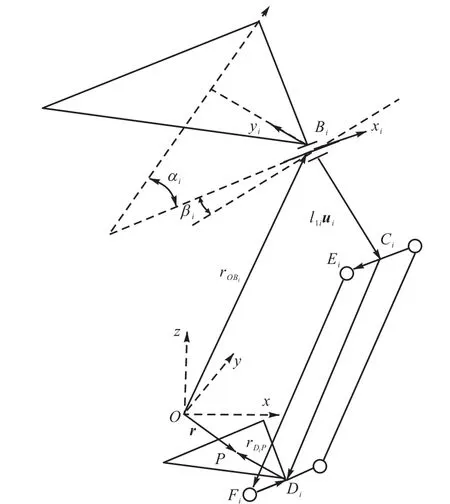
图2 Delta并联机构坐标系Fig.2 Delta parallel robot coordinate
唐国宝等[7]针对该机构的末端精度进行了理论方面的探讨,指出影响该机构末端精度的全部几何误差源在所建立的机器人坐标系下可由 36项参数表示,其中影响末端姿态精度的参数 12项,这些参数等价于从动臂支链的平行四边形结构对边是否平行,该机构中姿态误差属于不可控误差,因此需要通过合理制造装配工艺保证从动臂的平行四边形结构来抑制;影响机构末端位置精度的参数 24项,通过运动学标定可得到有效补偿.在保证从动臂平行四边形机构对边平行的基础上,可视从动臂为单杆,将 Ci、Di两点之间的距离视为从动臂的有效长度,记从动臂的有效长度为 l2i,单位方向矢量为 wi.同时,矢量rDiP、rOBi为常数,式(1)可简化为

式中:l2iwi= rCiEi+ rEiFi+rFiDi;bi= rOBi+rDiP.
记αi表示主动臂转轴轴线关于yz平面的结构角;βi表示主动臂转轴轴线xi关于xy平面的结构角;θi表示主动臂绕 xi轴的位置角,理论上 αi=−π / 6 + 2 π( i −1)/3,βi=0.影响该机构末端位置误差的24项几何参数包括:3项零点误差Δθ0i,3项轴向互成120°误差Δαi,3项主动臂驱动轴轴线相对静平台基准面平行度误差Δβi,9项主动臂转轴中点位置误差Δbi(即x向误差Δbix,y向误差Δbiy,z向误差Δbiz),3项主动臂杆长误差 Δ l1i,3项从动杆杆长误差 Δ l2i(i = 1 ,2,3),Delta并联机构的 24误差参数运动学逆解模型和运动学正解模型如下.
1.1 24参数运动学逆解模型
通过坐标系变换得到 ui:令 ui与y轴重合,然后将 ui绕z轴转动 αi−π2,之后再绕yi转动βi,最后再绕xi′轴转动θi.
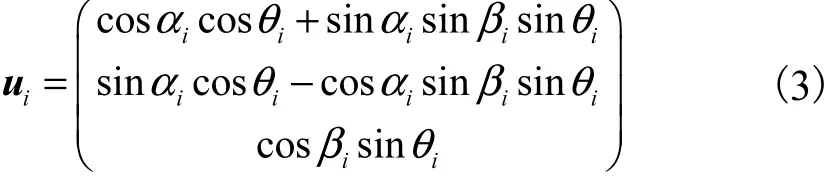
将式(2)改写为

两端同乘各自的转置,得

将iu带入式(5),并转变为三角函数式形式

式 中 : Ai= − 2 l1i[ (x − bix) sin αis i n βi+ ( y − biy) (− c osαi⋅sin βi)+(z − biz) cosβi] ;Bi= − 2 l1i[ (x − bix) cosαi+(y −biy)sinαi];
结合机构的装配模式,得

1.2 24参数运动学正解模型
将闭环方程(3)两端同乘各自的转置,得
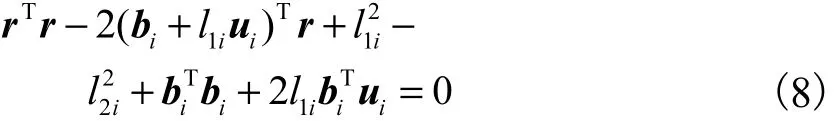
即

其中 r = [x,y,z]T,将式(9)展开可解得

2 机构误差参数辨识
2.1 误差源分析
影响Delta并联机构末端位置精度的24项几何参数是在建立的机器人坐标系下度量的,由于所涉及参数位置关系之间的相对性,它们之间存在一定的相关性,即建立Delta机器人坐标系Oxyz时:
(1) 若坐标系Oxyz原点平移ΔT ,B1、B2、B33点位置矢量误差同时变化ΔT;
(2) 若坐标系Oxyz绕z轴旋转Δθ,α1、α2、α33个结构角误差同时变化Δθ;
(3) 若坐标系Oxyz绕 x轴或 y轴旋转一定角度,B1、B2、B33 点和α1、α2、α33 个结构角也同时产生联动的误差.
因此,可按照如下条件建立 Delta机器人坐标系Oxyz:
(1) 坐标系Oxyz的 xy平面同机构 B1、B2、B33点所在平面平行;
(2) B1点位置矢量无误差,即 Δ bi=0;
(3) 支链 1主动臂转轴轴线关于z轴的结构角无误差,即Δα1=0.
此时,影响 Delta并联机构末端位置精度的几何误差参数可简化为 18项,如表 1所示,“√”表示需要标定计算的误差参数,“×”表示该项误差参数为0,不需要标定计算.

表1 Delta并联机构几何误差源Tab.1 Delta parallel robot geometric errors
2.2 基于步进迭代法的参数辨识
运动学标定中的核心内容是根据所使用测量仪器的特点,以实测信息与理想模型输出之间的残差为构造误差辨识模型,进而识别几何误差模型,如图 3所示.

图3 运动学标定过程Fig.3 Kinematic calibration process
将前述 Delta并联机构的正解和逆解映射关系分别表示为

式中:p为真实的几何参数集合{θ0ibil1il2iαiβi}(i =1,2,3);q为主动关节变量{θi}(i= 1 ,2,3).由于几何误差源的存在,p中各参数实际有效值同设计值之间存在一定的偏差,设 p =p0+Δp,p0表示理想模型中的几何参数集合,Δp为几何参数误差.为了辨识几何误差参数Δp,本文借助激光跟踪仪为测量工具,提出一种步进迭代的参数求取方法.方法描述如下.
在 Delta并联机构理论工作空间中选取 n个测点,各测点的主动关节变量 qi可以通过机构理论模型位置逆解获得,控制机构末端运行至所选取测点处,用激光跟踪仪测量其在激光跟踪仪坐标系下的空间坐标.设任意 2个测点在机构正解模型下的位置坐标分别为 ri和 rj,在激光跟踪仪坐标系下的实际坐标为 Ri和 Rj.如图 4所示,Oxyz表示基于正解模型的坐标系,为误差坐标系,图中用折线表示,OwXwYwZw表示激光跟踪仪坐标系.

图4 2个测点在2个坐标系下的度量Fig.4 Coordinates of 2 points under two coordinate systems
定义残差

定义误差评价函数

理论上存在某一Δp使得L=0,但是由于不可补偿误差、测量误差等因素的影响,在实际计算时以 L最小为原则来计算Δp.步进迭代法求取Δp过程如下.
步骤 1定义各误差参数初始值 Δ p = [ Δp1Δp2…Δpn]和初始搜索步长 s tep = [s1s2…sn],并由式(13)求取L.
步骤 2 重新确定step,方式如下:对于step的第k个参数,令 Δ pk=Δpk+ ξ ,将 Δ p= [ Δ p1… Δ pk… Δ pn],代入式(13),求取 L′( k =1,2,… ,n)
若 L ′≤L,sk≥0,则sk←1.5sk;
若 L ′≤ L ,sk<0,则 sk← − 0 .5sk;
若 L ′>L,sk≥0,则sk← − 0 .5sk;
若 L ′>L,sk<0,则sk←1.5sk.其中ξ为一微小量,确定step后,令Δ p = Δ p + step,重新求取L.
步骤3 判断step模值,即
若step > ζ,重复步骤2
若step ≤ ζ,循环结束,此时Δp即为最终结果,其中ζ为一微小量.不失一般性,在Δp求取时,定义初 始 值 Δp = [00 … 0 ],初 始 搜 索 步 长 s tep=[0.010.01…0.01],微小量ξ = ζ = 1× 1 0−5.
以任意两点距离理论值和测量值之间的残差定义评价函数,通过迭代的方式计算几何误差参数,同通用方法相比,省去了牛顿-高斯法求取误差雅可比矩阵的过程,算法更为简单.
3 实 验
实验所用 Delta并联机构主动臂和从动臂名义长度l1i= 3 50mm,l2i= 9 50mm,主动臂转轴中心位置矢量模长名义尺寸bi=149mm.制造装配时已经保证了末端动平台姿态误差较小(0.1,mm/m),标定前首先用水平仪将机械手3个主动臂置水平,并将该位置定为机械手初始零点.标定前先用激光追踪仪检测该并联机构末端在工作空间多个点位的定位精度,测量结果为:平均体积误差 0.73,mm,最大体积误差2.52,mm.
设计标定测量点位在理想模型中坐标如表 2所示,同时用激光跟踪仪测量机构末端在各个点位时激光跟踪仪坐标系下的实际空间坐标(见图 5),测量结果如表3所示.

表2 测点理论坐标Tab.2 Points’ coordinates under robot-coordinate system mm
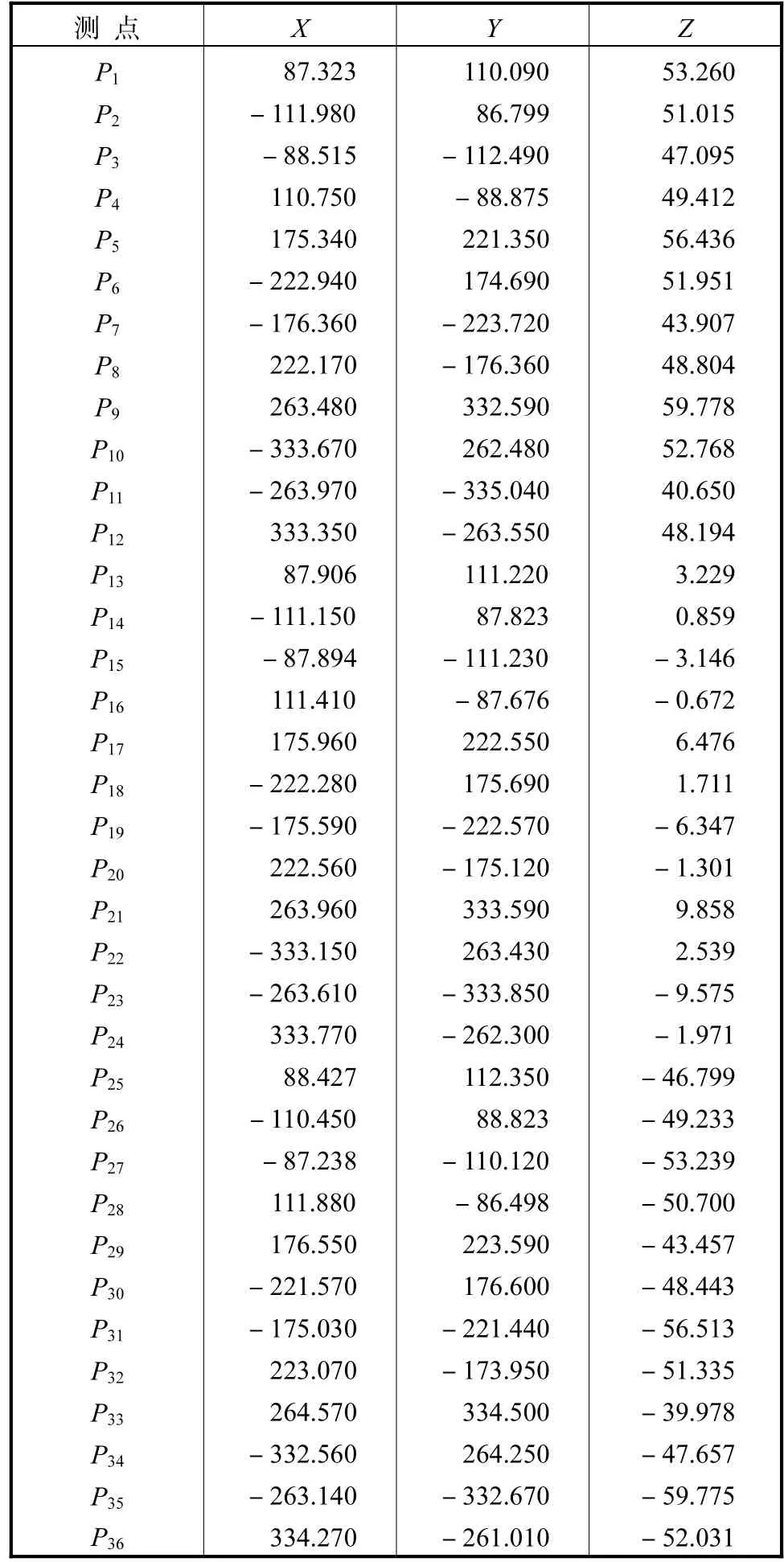
表3 激光追踪仪测量各点位空间坐标Tab.3 Points′space coordinates under laser trackercoordinate system mm

图5 激光追踪仪检测标定点空间坐标Fig.5 Measurement by laser tracker
利用第 2节所述误差参数辨识方法进行误差参数辨识,辨识结果如表 4所示.利用辨识出的误差参数修正 Delta并联机构的运动学模型,利用激光跟踪仪重新检测其末端的定位精度,测量结果为:平均体积误差0.06,mm,最大体积误差0.26,mm.对18项几何误差进行辨识补偿后,Delta并联机构精度得到大幅度提高,证明了所提方法的有效性.

表4 误差源参数辨识结果Tab.4 Identification results of geometry errors
4 结 论
(1) 建立了 Delta并联机构运动学模型,对影响Delta并联机构末端精度的几何误差源进行了分析,指出这些误差源可以简化为18项.
(2) 以激光追踪仪作为测量工具,设计了一种步进迭代的误差参数辨识方法,该方法简单高效,便于实施.并进行了标定实验,标定前,Delta并联机构平均误差 0.73,mm,最大误差 2.52,mm.标定补偿后Delta并联机构精度大幅度提高至平均误差0.06,mm,最大误差0.26,mm.
[1] 李占贤. 高速轻型并联机械手关键技术及样机建造[D]. 天津:天津大学机械工程学院,2004.Li Zhanxian. The Key Technologies and Prototype Development of High-Speed and Light-Weight Parallel Manipulator[D]. Tianjin:School of Mechanical Engineering,Tianjin University,2004(in Chinese).
[2] Chiu Yu-Jen,Perng Ming-Hwei. Self-calibration of a general hexapod manipulator with enhanced precision in 5-DOF motions[J]. Mechanism and Machine Theory,2004,39(1):1-23.
[3] 邵珠峰,唐晓强,王立平,等. 平面柔性3-RRR并联机构自标定方法[J]. 机械工程学报,2009,45(3):150-155.Shao Zhufeng,Tang Xiaoqiang,Wang Liping,et al.Self-calibration method of planar flexible 3-RRR parallel manipulator[J]. Journal of Mechanical Engineering,2009,45(3):150-155(in Chinese).
[4] 常 鹏,李铁民,刘辛军. 平面三自由度冗余并联机床的分步自标定方法[J]. 清华大学学报:自然科学版,2008,48(5):808-811.Chang Peng,Li Tiemin,Liu Xinjun. Setp-by-step selfcalibration of a 3-DOF planar parallel kinematic machine tool with actuation redundancy[J]. Journal of Tsinghua University:Science and Technology,2008,48(5):808-811(in Chinese).
[5] Besnard S,Khalil W. Calibration of parallel robots using two inclinometers[C]//Proceedings of 1999 IEEE International Conference on Robotics and Automation.Detroit,Michigen,USA,1999:1758-1763.
[6] Soons J A. Error analysis of a hexapod machine tool[J].Transactions on Engineering Sciences,1997,16:347-358.
[7] 唐国宝,黄 田. Delta并联机构精度标定方法研究[J]. 机械工程学报,2003,39(8):55-61.Tang Guobao,Huang Tian. Kinematic calibration of Delta robot[J]. Chinese Journal of Mechanical Engineering,2003,39(8):55-61(in Chinese).
[8] Huang Tian,Chetwyne D G,Whitehouse D J,et al. A general and novel approach for parameter identification of 6-DOF parallel kinematic machines[J]. Mechanism and Machine Theory,2005,40(2):219-239.
[9] Chang Peng,Wang Jinsong,Li Tiemin,et al. Step kinematic calibration of a 3-DOF planar parallel kinematic machine tool[J]. Science in China,Series E:Technological Sciences,2008,51(12):2165-2177.
[10] 刘大炜,王立平,关立文. 一个特殊 3自由度并联机构的精度分析及标定[J]. 机械工程学报,2010,46(9):46-51.Liu Dawei,Wang Liping,Guan Liwen. Accuracy analysis and calibration of a special 3-DOF parallel mechanism[J]. Journal of Mechanical Engineering,2010,46(9):46-51(in Chinese).
[11] Rauf A,Pervez A,Uchiyama M. Experimental results on kinematic calibration of parallel manipulators using pose measurement device[J]. IEEE Transactions on Robotics,2006,22(2):379-384.
[12] Alberto T,María S J,Eduardo C,et al. One camera in hand for kinematic calibration of a parallel robot[C]//23th IEEE/RSJ 2010 International Conference on Intelligent Robots and Systems. Taipei,China,2010:5673-5678.

