实时子步积分算法的设计与实现

王 宇，孙永维，宋省身，史云龙

（1.空军航空大学 军事仿真技术研究所，吉林 长春 130022；2.空军航空大学 飞训基地，吉林 长春 130062；3.空军航空大学 航空航天情报系，吉林 长春 130022；4.中国空气动力研究与发展中心 四川 绵阳 621000）

实时子步积分算法的设计与实现

王 宇1，孙永维2，宋省身3，史云龙4

（1.空军航空大学 军事仿真技术研究所，吉林 长春 130022；2.空军航空大学 飞训基地，吉林 长春 130062；3.空军航空大学 航空航天情报系，吉林 长春 130022；4.中国空气动力研究与发展中心 四川 绵阳 621000）

积分算法是实时仿真的关键所在，传统的单步法结构简单，但精度较差。而多步高阶积分算法虽然精度高，却由于结构复杂实时性不强。文章在对实时仿真积分算法研究的基础上，提出了实时子步积分算法，使不同的积分算法拥有相同的子步控制结构。由于每个子步的运算量一样，所以在步长和帧数一致的情况下，不同的积分算法运算时间是一致的。经仿真实验表明，该算法的子步结构显著提高了多步积分法的实时性，且误差精度在可控范围内。

计算机仿真；实时性；子步积分算法；子步控制结构

进行实时仿真试验时，仿真计算机与实物相连，仿真计算机必须在与真实系统同步的条件下获取动态输入信号，并实时地产生动态响应。要实现实时仿真，必须采取相应的实时仿真算法。而实时仿真中采用的算法需要有快速性、可取性、可靠性和相容性等特性[1]。传统的单步积分法由于其步长易控性并有较好的实时性，在实时仿真中应用较多，但是计算精度较差。多步积分法虽然计算精度高，但是计算步骤较复杂，实时性不强。

文中通过分析多种常用积分法结构，首次提出了实时子步积分算法，该算法利用特殊的子步结构改进了几种常用积分法，有效地整合了单步法与多步法的优点，使新算法具有较好的实时性和精度[2]。

1 通用数字仿真算法

仿真算法在数字仿真的各个阶段起着核心和支撑作用，一个好的仿真算法不仅能耗费较少的时间，而且也能得到比较高的精度。算法选择是实时数字仿真首先碰到的问题，选择合适的仿真算法可以使实时数字仿真以足够的精度顺利完成实验任务。否则将会事倍功半，甚至在试验过程中遭受种种挫折，严重影响进度和质量。

1.1 单步法

单步法中比较典型的有Runge-Kutta算法 （简称RK法）[3]。

一般的s级RK法有如下的形式：

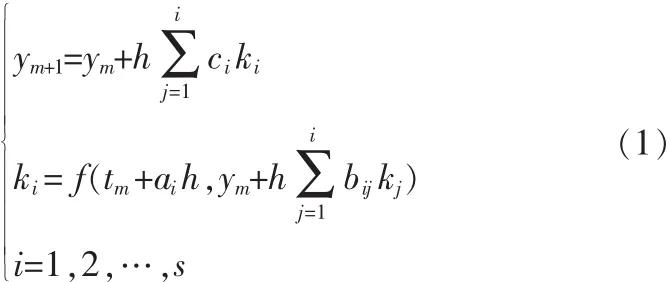
最常用的Runge-Kutta法为四阶RK法，亦称为经典RK法：

RK法的主要特点是计算tm+1点的值时，只需要用到tm点的值。其基本思想是在[tm，tm+1]内多计算几个点的斜率值Ki，然后将它们加权平均作为平均斜率K*，以构造出具有更高精度的计算格式。显式RK法在计算时，只用到K1，K2，…，Ki-1了的值。 而隐式 RK法在计算Ki时，不仅用到了 K1，K2，…，Ki-1的值，还可能用到Ki，Ki+1的值。显然显式RK法具有很好的实际意义。针对不同的需求，通过应用Taylor级数匹配原理来确定公式中的参数值，可以构造出各种RK法的公式。

1.2 线性多步法

Adams法是一种比较特殊的线性多步法。它计算ym+1的值，用到了 tm，ym的值和时刻 tm以前的导数值 fj=f（tj，yj），j＜m。Adams法也分为显式和隐式2种。显式Adams法是线性k+1步算法而隐式Adams法是线性k步算法。

例如四阶Adams显式（Adams-Bashforth，简称AB法）：

线性多步法比较典型的算法为Adams法[4]：

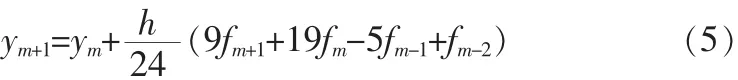
为了进一步提高算法精度，又提出了基于AB法和AM法的Adams预估-校正法，利用AB法作预估，再用AM法作校正，以四阶为例：

四阶 Adams隐式（Adams-Monlton，简称AM法）：

1.3 单步法与多步法的比较

由于单步法和线性多步法采取了不同的策略来提高仿真算法的精度，因而可以对它们进行对比研究[5]。

①单步法在计算ym+1的值时只用到ym的值，不需要ym-1，ym-2，…，各项的值，即单步法最大的特点是可以自启动，而多步法计算 ym+1需要用到 ym，ym-1， …，ym-k+1以及对应的 fm，fm-1，…，fm-k+1的值，所以要占用额外的储存空间来保存前k个yj和 fj的 值[6-7]。

②多步法计算ym+1，需要计算多个右函数来给出ki值。

③当进行变步长运算时，单步法使用灵活，高阶多步法相对来说计算复杂，因此在实时仿真中多用到单步法。

在基于控制系统的数字计算机中，由于对实时性要求强，多采用单步法来计算，这大大限制了算法的选择性，本文针对这个问题，提出了实时子步积分算法[8]。

2 子步积分算法

2.1 设计思想

根据常用的几种积分算法，我们利用子步积分结构改进四阶以内的 Adams显式（AB）法，Adams预估-校正（ABM）法和Runge-Kutta（RK）法。首先，把每种积分方法都划分成五个积分子步$IR1—$IR5，如表1所示。

表1 子步积分法存储结构Tab.1 The storage structure of Substep integral method

其中$IR1列为每种算法的启动项，当选择了某种算法，该算法即按$IR1->$IR2->$IR3->$IR4->$IR5->$IR2…依次循环推进，直到仿真结束。积分子步每向前推进一步，则计算一次右函数。以下是几种经改进算法的具体结构设计。

2.1.1 AB 法

AB法的4个积分子步都是相同的，以四阶的AB4法为例：i、ABST（算法启动）

启动了AB算法，设置了帧n-1的导数值xpa、帧n-2的导数值xpb和帧n-3的导数值xpc，使之全部等于右函数xp的初值。

xl为长字，用来储存计算结果，step_time为积分步长。

推进导数值的更新，并由前三帧导数计算帧n+1的值。

另外三种不同阶的AB法设计思路相同，只是右函数计算项p->xl有所不同。

2.1.2 ABM法

由于ABM为预估-校正算法，需要两帧一输出，以四阶ABM4法为例：

1）ABMST（算法启动）

启动了ABM算法，与AB初始条件设置一样，由于为两帧一输出，故步长为AB法的两倍。

经过预估-校正，在ABMP4计算结果，另外三种不同阶的ABM法设计思路也相同。

2.1.3 RK4法

RK法需要计算的值，四帧一输出，以4阶RK法为例：其步长为ABM法的2倍，即为AB法的4倍。

4个子步中的p->xpa分别计算了，然后在RK44中p->xl计算结果。

2.1.4 小 结

通过循环积分子步的设计，不同的积分法有了相同计算结构，统一了计算量的大小。同时根据伪代码的设计，每个子步都可以通过p->xl输出计算结果，大大增强了算法的实时性。

2.2 设计流程

根据仿真系统的控制结构的需求分析，编写算法的流程，如图1，主要设置了7个子模块，分别是：

1）#input（ ）

#input的主要功能是控制程序的输入，从in.dat文件读入变量的初值，和步长、帧数、维数以及算法的选择。

2）#ici（ ）

#ici的主要功能是储存变量的初值xi，并把子步积分控制顺序的变量index初始化为1，好进行积分子步的推进。

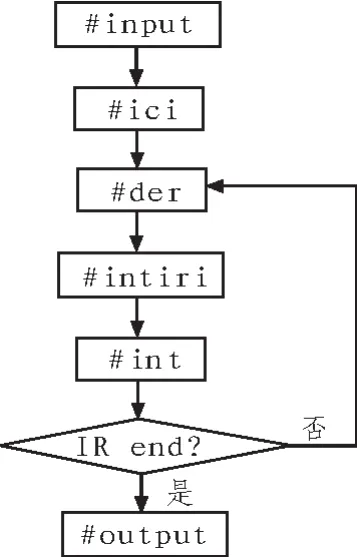
图1 算法流程图Fig.1 Algorithm flow chart

3）#der（ ）

#der的主要功能有2个，一是储存方程，二是在程序运行中求导函数，所以统一的方程格式是xp=···（xp代表变量x的导数），变量的导数就等于等号右边。由于方程不局限于一维，所以用数组形式 xp[0]=···，xp[1]=···，···，xp[n]=···来储存方程组。这样，方程的储存和读入，以及变量右函数求导问题就解决了。

4）#intiri（ ）

#intiri的主要功能是进行积分子步的控制，由1，2，3，4，5，2，3，4，5，2，3，4，5…的顺序向前推进。

5）#int（ ）

#int的主要功能是储存10种积分算法，在程序需要调用计算积分的时候，按照需求，提供相应的积分子步，完成程序的计算。

6）#output（ ）

#output的主要功能是把输出变量的积分数值到out.dat文件。

7）#init（ ）

#init的主要功能是初始化分配内存。程序的数据结构应该包括：xl（长字）、xi（初值）、xp（导数）、xpa（前一帧导数）、xpb（前二帧导数）、xpc（前三帧导数）、method（积分方法），所以我们可以把数据结构定义为：

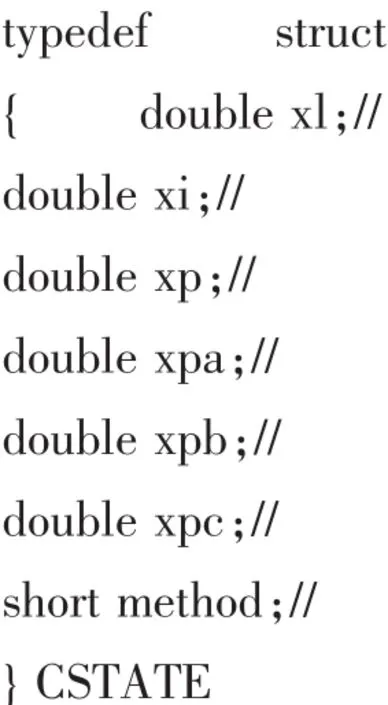
根据要求，把前6个参数定义为双精度，积分算法为单精度就可以。

3 测试对比

MATLAB求解常微分方程组主要应用ODE函数，利用具有非线性扰动的非线性Van Der Pol方程来进行测试，

van der pol微分方程[9]：

在步长一定的情况下，把实时仿真得到的结果与MATLAB的结果进行对比，这里选择3种代表性的算法AB4、ABM4和RK4法测试。

3.1 仿时真间

由于子步积分算法结构统一，所以在步长和帧数一致的情况下，不同积分算法的仿真时间是一致的，这是子步积分算法最大的特点。

3.2 误差分析

我们实验仿真步长为0.01，帧数为100，对比3种子步积分算法的输出结果与对应的MATLAB算法输出结果，分析数据可知，3组对比结果存在一定的误差，且误差都在稳定误差区间内，根据算法结构分析，误差产生的原因与算法精度的设置有关。

通过对比数据曲线图，我们发现图2中4条数据曲线基本拟合；图3中数据曲线每隔一点分离、重合一次，可知分离点为ABM4法的预估部分，重合点为ABM4法的校正部分；图4中数据曲线每隔三点分离、重合一次，因为RK4法每四步输出一次结果。

对输出数据进行差值对比，对比方式为AB4法每帧对比，ABM4法隔一帧取值，RK4隔三帧取值，计算3组差值的方差，如表2所示。

可以看出，AB4->ABM4->RK4差值的波动越来越小，趋于稳定，误差逐渐减小，精度变高。实验结果证明实时子步积分方法是可行的，得到的结果与预期一致，算法的结构设计比较成功。

图2 AB4法输出数据对比曲线Fig.2 Output data contrast curve of AB4

图3 ABM4法输出数据对比曲线Fig.3 Output data contrast curve of ABM4

图4 RK4法输出数据对比曲线Fig.4 Output data contrast curve of RK4

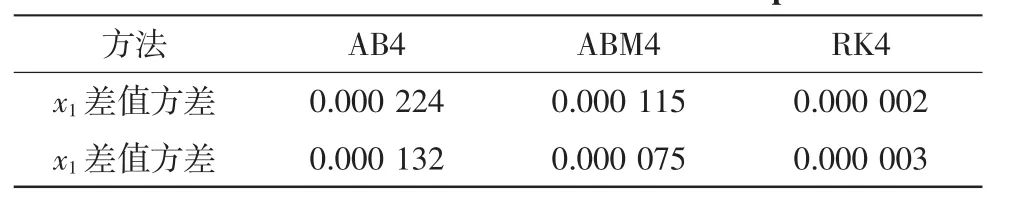
表2 输出结果差值方差Tab.2 Difference values variance of output

4 结 论

文中分析了几种常用的积分算法，提出的实时子步积分算法结构，改进了几种常用积分算法，很好地解决了实时仿真中的变步长计算和运算量不一致问题。使得积分算法的选择不再局限，增强了在工程计算上的扩展性。实现了算法的程序编写，经与MATLAB仿真结果对比，验证了子步积分算法的精确性，分析了误差的产生原因。该算法结构为控制领域的工程实践提供了一个很好的设计思想，而如何结合实时仿真控制系统将是下一步研究方向。

[1]刘怀，费树岷.控制系统中实时任务的动态优化调度算法[J].控制与决策，2005，20（3）：246-250.

LIU Huai，FEI Shu-min.Optimal dynamic scheduling algorithm for real-time tasks in digital control systems[J].Control and Decision，2005，20（3）：246-250.

[2]王永炎，王强，王宏安，等.基于优先级表的实时调度算法及其实现[J].软件学报，2004，15（3）:360-370.

WANG Yong-yan，WANG Qiang，WANG Hong-an，et al.A real-time scheduling algorithm based on priority table and its implementation[J].Journal of Software，2004，15（3）:360-370.

[3]Marti P，Fohler G.Jitter compensation for real-time control system[J].Proceedings of the 22nd IEEE Real-time System Symposium，2001，19（2）:139-148.

[4]刘德贵，朱珍民.实时仿真算法的研究进展[J].系统仿真学报，2003，24（2）:134-136.

LIU De-gui，ZHU Zhen-min.Research advance for real-time simulation algorithms[J].Acta Simulata Systematica Sinica，2003，24（2）:134-136.

[5]黄振全.实时数字仿真算法的研究[M].南京：东南大学2006.

[6]金士尧，党岗，凌云翔，等.银河高性能分布仿真系统的设计和实现[J].计算机研究与发展，2001，29（2）:457-459.

JIN Shi-yao，DANG Gang，LING Yun-xing，et al.Design and implementation of YH high performance distribute simulation system[J].Journal of Computer Research and Development，2001，29（2）:457-459.

[7]金宏，王宏安，唐雪梅，等.计算机控制中的模糊调度设计[J].计算机学报，2006，29（3）:414-422.

JIN Hong，WANG Hong-an，ANG Xue-mei，etal.Fuzzy scheduling design in computer control[J].Chinese Journal of Computers，2006，29（3）:414-422.

[8]Stankovic J，Ramamritham K.The spring kernel:a new paradigm for real-time systems[J].IEEE Software，1991，8（3）:62-72.

[9]王震，孙卫.多自由度Vanderpol振子极限环计算[J].计算机工程与应用，2011，45（2）:85-89.

WANG Zhen，SUN Wei.Computingforlimitcycleof Vanderpoloscillatorwith multidegree offreedom[J].Computer Engineering and Applications，2011，45（2）:85-89.

Design and realization of real-time substep integral algorithm

WANG Yu1， SUN Yong-wei2， SONG Xing-shen3， SHI Yun-long4
（1.Dept.of Military Simulation Technology Institute， Aviation University of AirForce， Changchun 130022， China；2.Dept.of Base of Flight Training， Aviation University of AirForce， Changchun 130062， China；3.Dept.of Aeronautics and Astronautics Intelligence， Aviation University of AirForce， Changchun 130022， China；4.China Aerodynamic Research and Development Center， Mianyang 621000， China）

The integral algorithm is the key point in real-time simulation， and traditional single-step algorithms is simple， but the accuracy is poor.The multi-step high order integral algorithms have high accuracy，but the complicated structure make poor real-time nature.Based on integral algorithms for real-time simulation，this paper put forward the real-time substep integral algorithms，to make different integral algorithms has the same substep control structure.For every substep has the same calculations，different integral algorithms have the same runtime under the same step length and frame number.Experiments show that the substep control structure significantly enhances the timeliness of Multi-step integral algorithms，and the error precision is under control.

computer simulation； timeliness； substep integral algorithms； substep control structure

TP391.9

A

1674－6236（2013）08-0053-05

2012-12-10稿件编号201212059

王 宇（1988—），男，吉林吉林人，硕士研究生，助理工程师。研究方向：虚拟仿真。