浅谈排课系统中遗传学算法的应用

苏 晨

（长春金融高等专科学校 办公室，吉林 长春 130028）

一、引言

信息化管理系统的概念于1961年由美国人J.D.GALLAGHER首先提出，是一门新兴的集管理科学、信息科学、系统科学及计算机科学为一体的综合性学科，研究的是企业中信息管理活动的全过程，以更有效地进行信息化管理。该系统中具体的操作环节都是通过算法应用和框架的搭建来完成的，遗传学算法也是最常用的算法之一。

二、遗传学算法在排课系统中的应用

在排课系统里，首先要做的工作是将教师、学生、教室、时间几个有机的条件和因素合理地安排在一个时间周期里，并且保证在运行的过程中不产生冲突。合理地排课可以使学校有限的教学资源利用率最大化，科学有序地将教学工作更好地推进下去。

（一）排课系统中容易起冲突的因素

因素1：星期一至星期日共7天，但只有5天能安排课时。一天当中上午有2个课程时段，下午也有2个课程时段，同一门课程在一天当中不要重复安排，避免学生产生厌烦感。

因素2：每一门课程都有几个老师来讲授，并且课程都有它的编号和所属院系，不同种类的课程上课地点也不同。

因素3：每个班级在同一时间段只能安排一个地点和教室上课，并且只能由同一名老师讲授同一门课程。

因素4：同一时间段只能有一个班级和老师占用。

因素5：同一时间段只能安排一个教室和班级。[1]

通过以上分析，我们可以总结出以下一些约束条件，这样系统运行起来就不会产生冲突。

（二）约束条件

1.同一个班级在合理条件下一个课时段只能有一门课。

2.同一名老师在合理条件下一个课时段只能有一门课。

3.同一间教室在合理条件下一个课时段只能有一门课。

4.教室数量始终保持比课程的门数大。

另外，学校开设的公共课应当优先安排，从而保证绝大多数学生的根本利益。在一天里如果同一门课程需要重复安排的，原则上应该留有间隔时间，以保证学生能够充分地消化和吸收所学的知识。

（三）各种因素在数学公式中的表达

教师：A={A1，……AY}

A表示教师人数，那么，某一教师就是AX，1<=X<=教师总数。

班级：B={B1，……BY}

B表示班级个数，那么，某一班级就是BX，1<=X<=班级总数。

教室：C={C1，……CY}

C表示教室个数，那么，某一教室就是CX，1<=X<=教室总数。

课程：D={D1，……DY}

D表示课程门数，那么，某一课程就是DX，1<=X<=开设课程门数。

课表的集合函数可以表示为：

K={K11，K12，K13，K14，K15，

……

K71，K72，K73，K74，K75，}

综上所述，任何一个时间点的课表就可以表示为KMN，M表示星期几，M的范围为1至5；N表示第几节课，N的范围为1至6。

课表的形式如表1所示：

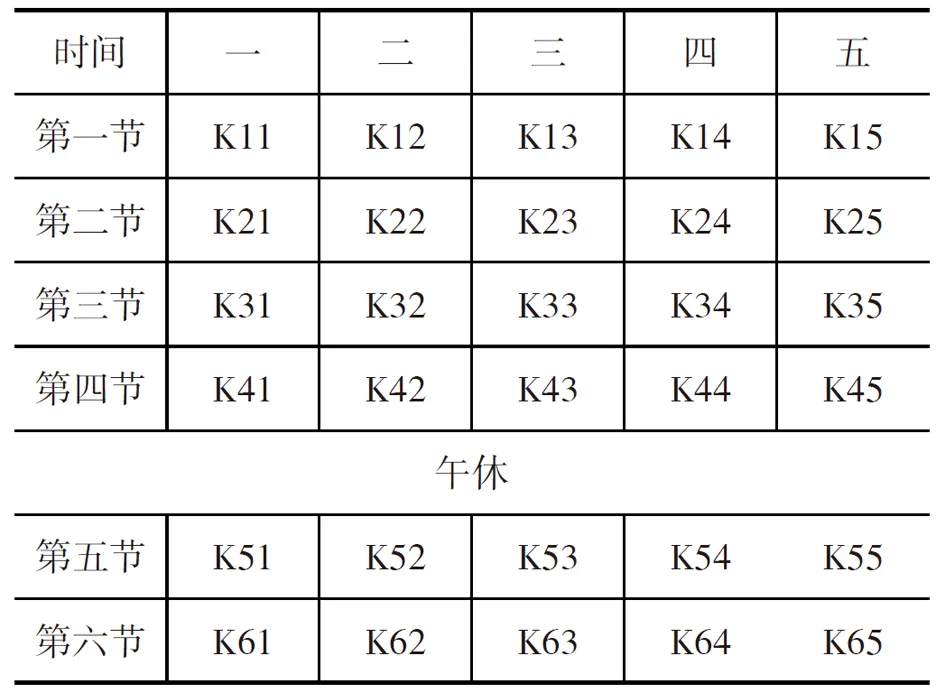
表1 课程表

例如，我校每个专业一般有4～5个班，周一至周五每天6节课，共30个时间段。下面以计算机系为例，如表2所示：

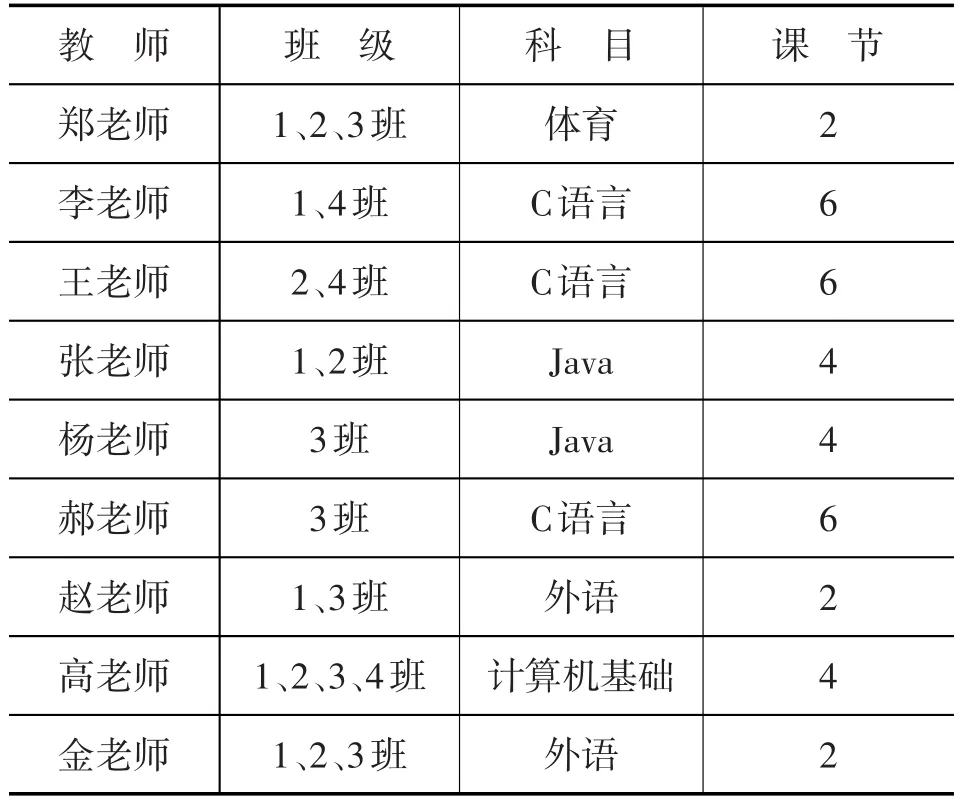
表2 课程表

根据教师姓名、所教班级、所教科目、随机的上课时间，每一条形成一条染色体，如“1247 1811 8017 22”，最终初始化一个课表，作为数据集。

如果同一课程在一周之内需要反复安排，那么相邻两次上课的时间应该有一定的间隔。基于这种情况，系统处理同一门课程之间的间隔要用相差1来表示二者的离散度。测试得出的期望值如表3所示：

表3 课程离散度期望值

系统通过函数运算计算出组合因子的时间差，首先把所有检测出的时间差对应的期望值函数求和，F（i）=（i=1，2，3，……35）。然后再随机选取两张期望值表，比较它们的适应度，删除适应度小的表，复制适应度大的表并进行替换。[2]

检测每一个班级和每一门课程的位置，也就是检查教师函数和课程函数在课表中数值分别是否为“l”，如果为1，则读取其中的时间片，求出期望值函数Fp（i）（i=1，2，3，4.....35）。

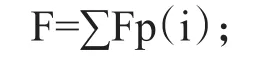
在这种函数分析中，我们可以得出以下适度函数：

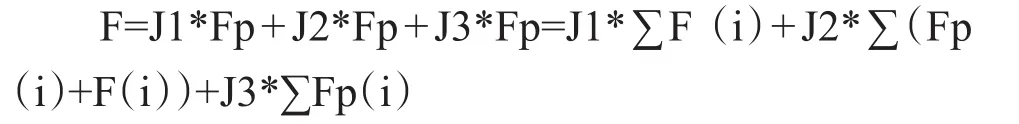
J1，J2，J3，是各种期望值对总期望值的参数。

依据以上的公式我们能得到适应度函数，并且做出冲突检测从而完全地消除冲突。在整个排课系统中冲突是必须要完全消除的；适应度函数的作用在于它的值越大，表明系统安排的课程在一定程度上越趋于适合实际教学情况。此外，如遇到其它具体问题时，还可以进行手工调整，以保证整个系统的合理、高效运行。

选择运算和变异运算是系统生成下一代种群的方式和方法，通过有限次的选择运算和变异运算找到最优解。假设变异的概率为Pm=0.25，小于1时会发生变异。例如，在系统中随机选两天，两天的时段互换，即周一和周二交换，那么：

2122是周二第1节和第2节，有25%的机率变化成2152，即周二第1节和周五第2节。

系统中这部分的主要代码为：

运用上述分析和程序，我们就可以将学校各班级的课程表合理地排出，并在教学中应用了。

三、总结

本文阐述了遗传学算法在排课系统中的应用，实践证明，遗传学观点的编码方式与数学当中的适度函数的结合应用是可行的。对于冲突的检测和消除达到了良好的预期效果，使得系统能稳定正常地运行。遗传学算法在信息化系统中的应用今后一定会越来越多，必将成为系统运算中的主流。

[1]吴金荣.解课程表问题的分支定界算法.硕士学位论文[D].北京：中国科学院数学与系统科学研究院，2002：14－16.

[2]何永太.二部图在排课系统设计中的应用[J].安徽水利水电职业技术学院学报，2003，21，（3）：45－47.

[3]胡顺仁，邓毅，王铮.基于高校排课系统中的图论问题研究[J].计算机工程与应用，2002，19，（4）：221－223.

[4]刘继清，陈传波.模拟退火算法在排课中的应用[J].武汉船舶职业技术学院学报，2003，6，（3）：45－46.

[5]李增智，王云岚，陈靖.课程表问题的一种混合型模拟退火算法[J].西安交通大学学报，2003，21（3）：45－47.

[6]孙曼.基于时间位图迭加匹配的课表编排算法[J].华东船舶工业学院学报，2002，19，（4）：221－223.

[7]陈本庆，马永强，何虎.改进型回溯法在高校排课中的应用[J].成都信息工程学院学报，2003，18，（2）：150－154.

[8]朱文兴，张千里.基于GENET的时间表问题自动求解算法[J].小型微型计算机系统，2003，6，（3）：45－46.