基于万有引力搜索算法的电厂锅炉NOx排放模型的参数优化

牛培峰， 肖兴军， 李国强， 马云飞， 陈贵林， 张先臣

（1.燕山大学 工业计算机控制工程河北省重点实验室，秦皇岛066004；2.国家冷轧板带装备及工艺工程技术研究中心，秦皇岛066004）

随着能源危机的日益凸显和人们对环境重要性认识的提高，节能、环保成为燃煤电力行业面临的永恒课题.目前，火力发电约占全国发电量的80%.我国对火电厂提出了一系列的改革措施和环保要求，要求大型电站锅炉在提高燃烧经济效益的同时，控制污染物向大气中的排放.因此，电站锅炉燃烧优化问题显得尤为重要.对于给定的电站锅炉，影响锅炉效率和NOx排放量的因素很多［1］，如煤质特性、锅炉负荷、炉温、配风方式、燃烧器型式、风粉配比和煤粉细度等，并且炉内燃烧过程非常复杂［2］，很难用机理模型去描述.对此，许多学者进行了多方面的研究工作［3］.

笔者提出基于万有引力搜索算法（Gravitational Search Algorithm，GSA）［4］和最小二乘支持向量回 归 机［5］（Least Squares Support Vector Regression，LSSVR）来进行综合建模.GSA是最近出现的一种新的寻优算法，应用原理为物体间的相互作用力即万有引力定律.LSSVR的建模方法通过利用结构风险最小化原理，使模型在学习和预测过程中具有很好的泛化能力.此外应用GSA算法能够很好地解决支持向量机中参数的选择问题.鉴于以上特点，笔者提出利用LSSVR建立电站锅炉燃烧优化模型，应用GSA来搜寻模型中的未知参数，并与遗传算法（Genetic Algorithm，GA）、蜂群算法（Artificial Bee Colony，ABC）和粒子群算法 （Particle Swarm Optimization，PSO）这3种智能算法进行了对比试验研究，为电站锅炉燃烧调整和降低污染物的排放提供了有效参考.

1 支持向量机建模原理

支持向量机（SVM）是Vapnik等人于1995年提出的.作为数据挖掘中的新方法，支持向量机应用结构风险最小化原则，能够有效地解决机器学习理论中的泛化问题.最小化结构风险目标函数能够有效地抑制模型建立过程中欠学习和过学习现象［6］，从而获得良好的泛化能力.该算法最终将转化为一个二次规划问题得到全局最优点，避免了应用神经网络设计的困难和结果不确定等问题以及在建模中出现局部极小值的问题.而最小二乘支持向量机将优化问题转化为求解线性方程组［7］的问题，其求解速度较快，求解所需计算资源较少，且目标函数的结构只与支持向量有关，这样就减少了计算量，加快了计算速度.该方法对于小样本学习具有很大的优势.

对于训练样本集T＝｛（x1，y1），…，（xl，yl）｝∈（X，Y）l，其中xi∈X＝Rn，yi∈Y＝R，i＝1，…，l；设其目标函数为f（x）＝ωx＋b，对其进行线性回归，设所有训练数据都可以在精度ε下无误差地用线性函数拟合，考虑到会有少数样本点的预测误差大于ε的情况，引入松弛因子ξi和两者都大于等于0），回归问题就可以转化为最小化结构风险函数的问题［4］：

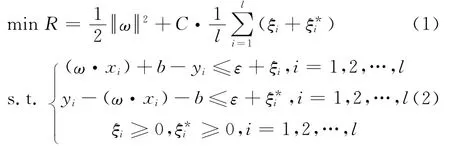
根据式（2）的约束条件，最小化式（1）即可求得目标函数中的ω和b［8］.

式（1）中第一项使回归该函数更为平坦，泛化能力更好；第二项则能够减小误差，其中C为惩罚系数且C＞0.yi样本实际值与f（xi）预测值的差值小于ε时，不计入误差大于ε时误差记为

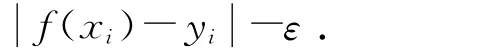
若要进行非线性回归，应首先通过非线性映射函数把数据映射到更高维的特征空间，再在高维空间进行线性回归，这样相对于原空间就是进行了非线性回归.设函数φ（xi）为非线性映射函数，则K（xi，xj）＝φ（xi）·φ（xj）是映射函数的点积，称此函数为核函数.Mercer定理证明，只需满足Mercer条件的对称函数即可作为核函数.在数据优化理论中Kuhn－Tucker定理说明，拉格朗日函数鞍点满足KKT互补条件，通过此条件可求得式（1）、式（2）的对偶问题，如式（3）、式（4）.因此求出对偶问题的解，就能求出原问题的解.对于LSSVR模型，将上述普通向量机的不等式约束条件改为等式约束条件即可.详细推导见文献［5］.

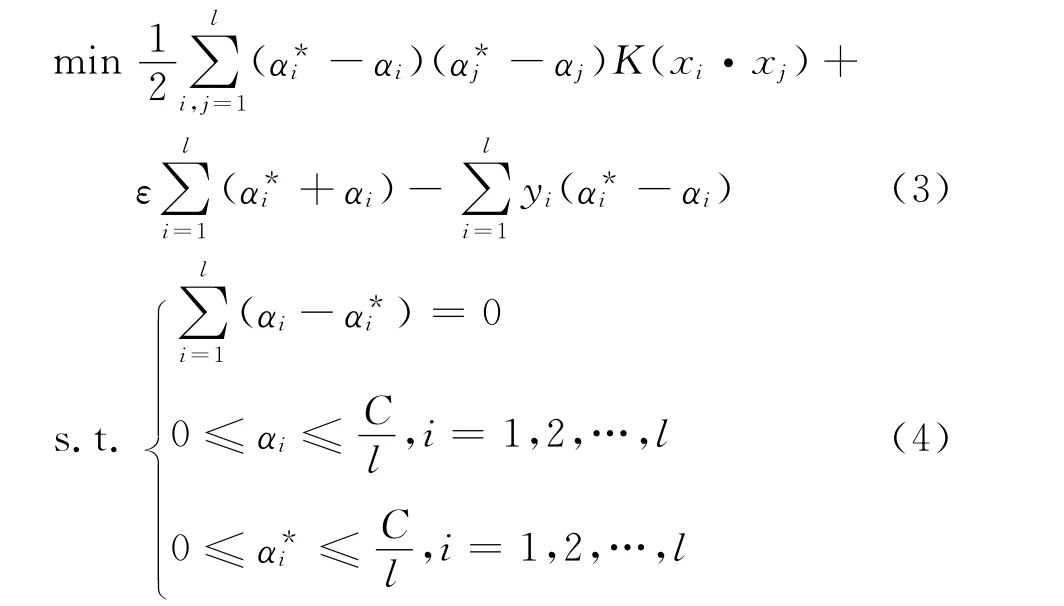
式（3）中的核函数 K（xi，xj）对于支持向量机来说非常重要，但是如何选择和确定核函数到目前还没有公认的理论依据.较常用的核函数有4种：线性函数、多项式函数、径向基函数和Sigmoid函数.根据文献［9］的描述，笔者选用径向基函数

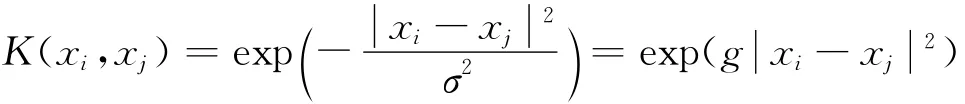
作为核函数.上述LSSVR模型中有一对参数（C，σ2）需要确定，下面将用新的方法进行参数（C，σ2）的确定.

2 万有引力搜索算法（GSA）

2.1 万有引力

GSA优化算法的原理来源于万有引力定律.万有引力是2个具有质量的物体间相互吸引的作用，两者之间没有仲裁者也没有时间的延迟.任何有质量的物体间都存在万有引力，两物体间引力的大小与它们质量的乘积成正比，与它们之间距离的平方成反比，其表达式如下

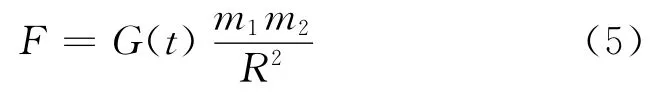
式中：R为两物体间距离；G（t）为万有引力常量.

G（t）的大小取决于宇宙的真实年龄［10］，表达式如下

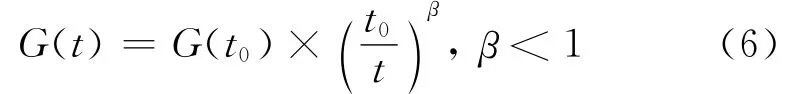
牛顿第二定律指出：当一个力F作用于一物体上时，此物体的加速度a取决于作用力F和物体本身的质量m，即：

由式（5）和式（7）可得，空间中的所有物体都存在相互作用力，质量越大、距离越近的物体间的相互作用力就越大（图1）.

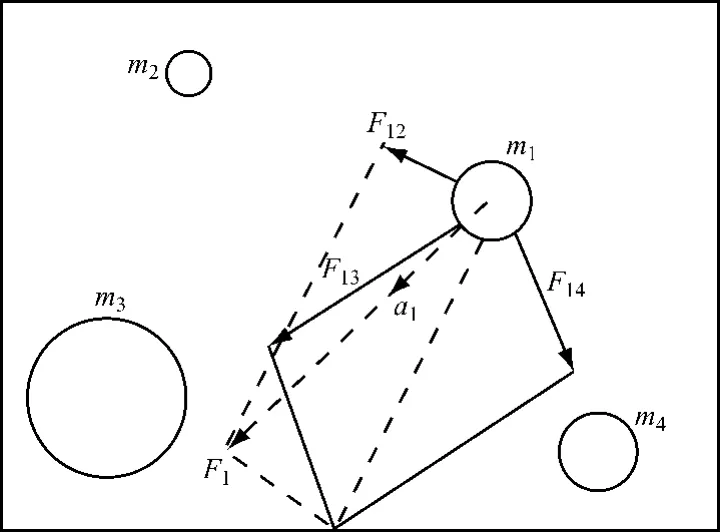
图1 各物体对m1的作用力Fig.1 The force generated by other objects on m1

2.2 GSA描述

在GSA中，相互作用的物体都被作为目标，通过计算与周围其他目标的性能来进行筛选，所有的目标之间都存在着万有引力，各个个体互相影响.相互作用力的存在使得所有个体整体移向具有最大质量的那个物体.因此，所有目标通过万有引力形成一系列信息链进行相互协调.大质量物体移动的速度比小质量物体移动的速度慢，这样能够保证搜索算法的步长，不易丢失最优解.

GSA中每一个个体都有4个描述特征：位置、惯性质量、主动引力质量和被动引力质量.个体的位置就相当于问题的最优解，它的惯性质量和被动引力质量可以看作是等价的.随着时间的增加，假设所有的物体都被较大质量的物体所吸引，当前物体的位置就是搜索空间中的最优解.

假设一个系统有N个个体，定义第i个个体为

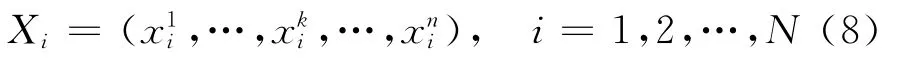
为简单起见，重新定义万有引力的表达式，在确定的时间t下，物体j对物体i的作用力为：

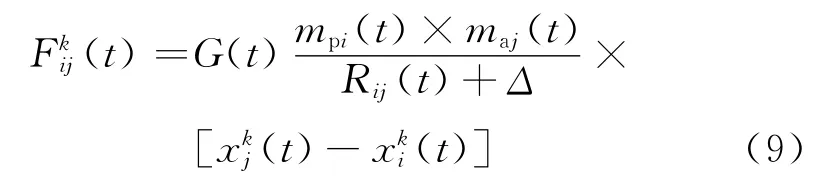
式中：ma为主动引力质量；mp为被动引力质量；i和j为个体序号；Δ为一较小的常数；Rij（t）为个体i和个体j之间的距离.

则所有物体对物体i作用力的合力为：

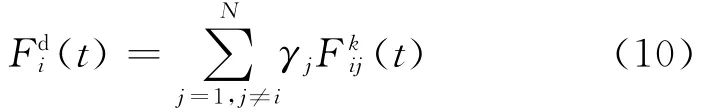
式中：γj是［0，1］中的一个随机数.

由此，通过运动定律计算出物体i在t时刻的加速度

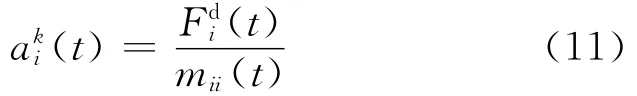
式中：mii为物体i的惯性质量.

根据力学中的运动公式进一步确定物体i的速度和位置，即：

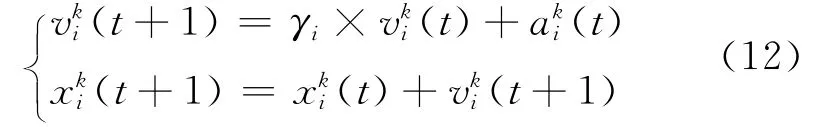
一开始万有引力常数G被初始化，随着算法的进行，G逐渐变小，从而控制算法搜索的准确度.引力质量和惯性质量通过适当的评价进行估算.大质量物体就是具有高适应度的个体，即适应度高的个体具有较大的吸引力和较慢的移动速度.假定引力质量和惯性质量相等，通过适当的运算规则来计算质量的大小.利用式（13）逐步更新引力质量和惯性质量：

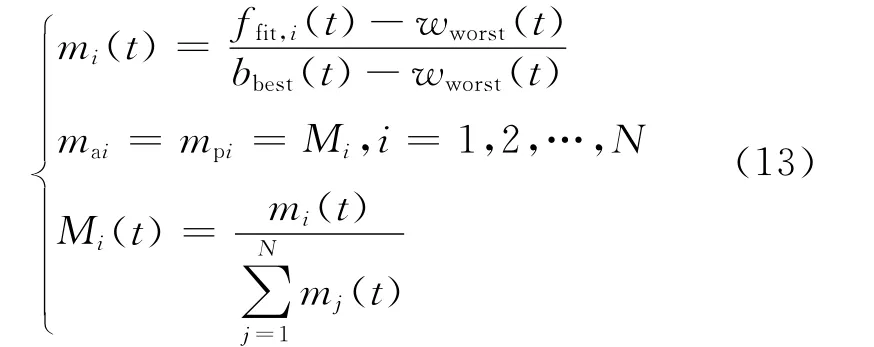
式中：ffit，i（t）是个体i在t时刻的适应度值；wworst（t）和bbest（t）定义如下

2.3 GSA步骤

根据上述描述，确定搜索算法的步骤如下：（1）指定搜索空间；（2）随机初始化参数；（3）个体适应度值的计算；（4）更新数据G（t），bbest（t），wworst（t）和Mi，i＝1，2，…，N；（5）计算参与者各个方向的作用力、加速度和速度；（6）更新个体位置；（7）判断是否达到要求，若是，搜寻结束，若否，跳转至步骤（3）.

3 NOx排放质量浓度LSSVR模型的设计与仿真

3.1 LSSVR模型的设计

锅炉的燃烧过程是一个复杂的物理化学过程，影响因素较多，且具有强耦合、非线性等特征，难以用机理模型来描述.而用支持向量机建立的模型为黑箱模型，模型输入输出之间的非线性函数关系可用支持向量来实现.由此，以某330MW煤粉汽包锅炉为测试对象，针对其NOx排放质量浓度进行多工况测试，对影响锅炉燃烧特性的各运行参数（如锅炉负荷、给煤机转速、一次风风速、二次风风速、燃尽风开度以及煤质特性）进行变工况试验，试验时煤粉细度保持不变.具体数据见表1和表2.

应用支持向量机针对该锅炉建立NOx排放质量浓度特性模型，在建模过程中，为了突出影响NOx的主要因素，暂未考虑飞灰含碳量对NOx排放质量浓度的影响.NOx排放质量浓度模型的输入参数选取如下：各工况中，一次风风速由甲、乙、丙、丁等4个参数表达；投运4台给煤机，4台给煤机转速由A、B、C、D等4个参数表达；一次风分别与4台给煤机一一对应，这4项用来描述一次风粉量对NOx排放质量浓度的影响；锅炉负荷由1个参量表达，作为1个输入参数；二次风共投入5层，同层联动，各层风速分别由燃烧器AA、AB、BC、CD和DE等5个位置的参数表达；燃尽风开度由OFA上、OFA下和SOFA 3个位置的参数表达；省煤器出口氧体积分数作为1个输入参数，用来描述燃烧氧体积分数对NOx排放质量浓度的影响；排烟温度作为模型的1个输入参数；煤种特性取w（Car）、w（Har）、w（Oar）、w（Nar）、w（War）、w（Aar）和发热量Qar等7个参数.共计26个操作量作为输入参数，将NOx排放质量浓度作为输出参数，其简化模型如图2所示.

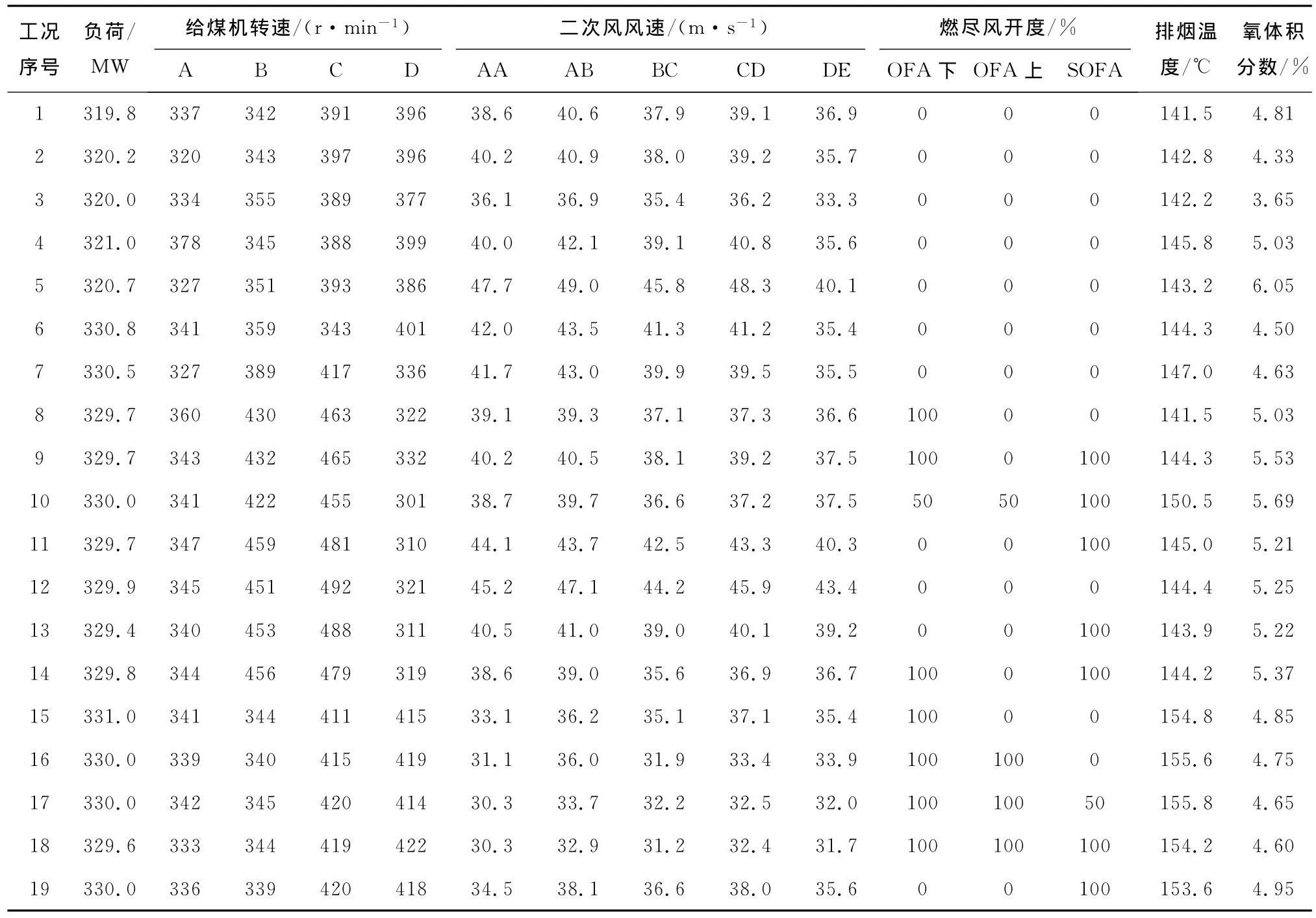
表1 锅炉运行测量数据Tab.1 Measurement data of boiler under various working conditions

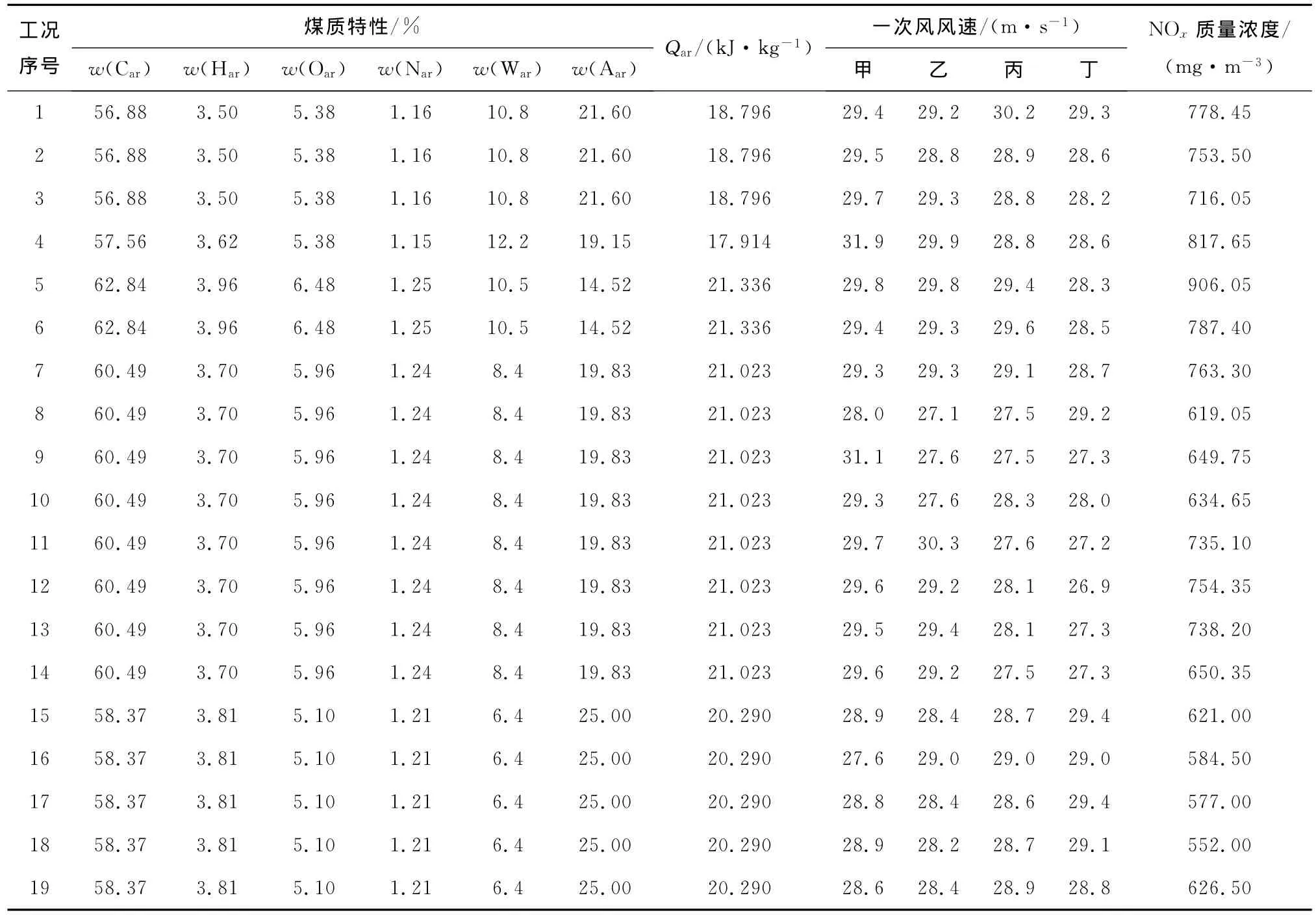
表2 锅炉运行试验数据Tab.2 Experimental data of boiler under various working conditions

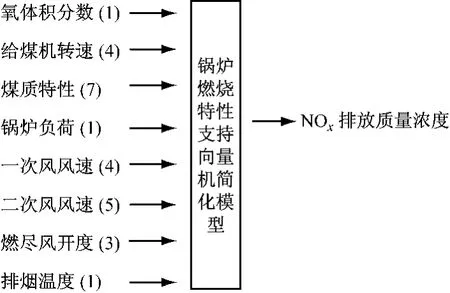
图2 锅炉燃烧特性支持向量机简化模型Fig.2 Simplified model by support vector machine for NOxemission

由于各输入输出参数值的范围相差较大，对所建模型的影响也较大，因此，在训练模型之前将相应的输入参数和输出参数进行归一化.

将GSA算法与支持向量机模型相结合来对锅炉燃烧系统参数进行优化，以降低NOx的排放质量浓度.首先，应用GSA算法对支持向量机模型中的惩罚系数C和核函数参数σ2进行优化，利用支持向量机回归预测原理对未参与训练的工况进行预测以验证模型的准确度与泛化能力.GSA算法的群体规模是根据参数范围的大小来进行选择的，参数C和σ2的限定范围如式（14）［11］，此外还需兼顾寻优速度，因此根据仿真试验可设定种群规模为50.

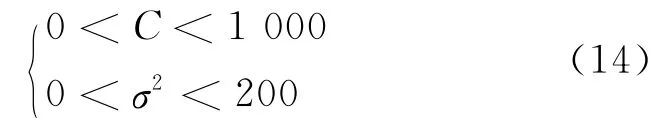
寻优算法的搜寻次数不宜过多，通过多次仿真试验，确定本试验循环次数为50次.在优化模型参数C和σ2时，优化目标为最小均方差，即其中i＝1，…，m；f（x）为参数向量［C，σ2］所建成的模型预测值；y为数据中的实测值.

3.2 仿真结果

利用LSSVR和GSA相结合的综合建模方法进行建模仿真，在表1的19组工况中，选取17组数据进行训练优化建模，其余2组作为预测数据，用来验证模型的准确度和泛化能力，预测数据为第1、第2组.在建模优化过程中，应用GSA搜索算法获得的适应度值如图3所示.

同时，获得最优参数（C，σ2）的值为（678.735 2，185.852 7），利用此组（C，σ2）作为支持向量回归模型的参数进行建模，对所选17组训练数据和2组预测数据进行回归预测，预测值见图4.为验证此算法在建模中的优越性，将此算法与另外3种智能算法的综合建模进行对比仿真试验，各方法全工况预测误差如图5所示.由图5可知，工况1和工况2中的数据未参与模型训练，其误差值相对于其他参与训练的工况而言较大，符合系统建模原理.其余17组工况都参与了模型训练，误差值较小，可用来检测模型的准确性.

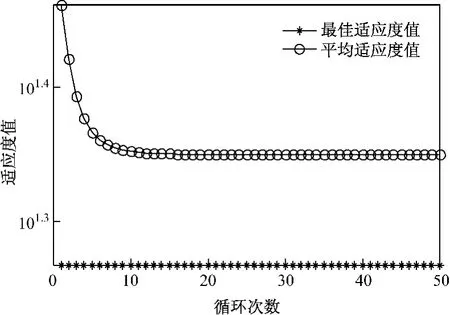
图3 适应度曲线Fig.3 The curve of fitness values

利用各种综合建模方法得到的工况1和工况2预测值与实测值的相对误差（Relative Error，Re）如表3所示.由表3可以看出，利用GSA寻优算法与LSSVR综合建模所构建的模型比利用其他智能算法与LSSVR综合建模所构建的模型具有更好的准确度和泛化能力.因而，GSA搜索算法更具有预测推广价值.

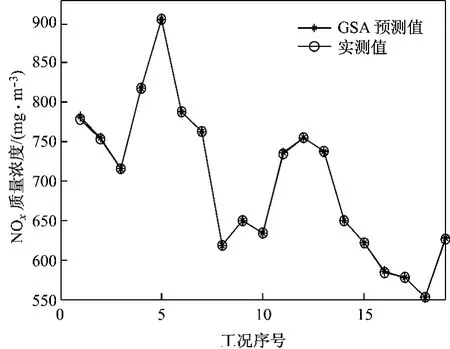
图4 GSA预测值与实测值的比较Fig.4 Comparison of NOxemission between actual measurements and GSA prediction

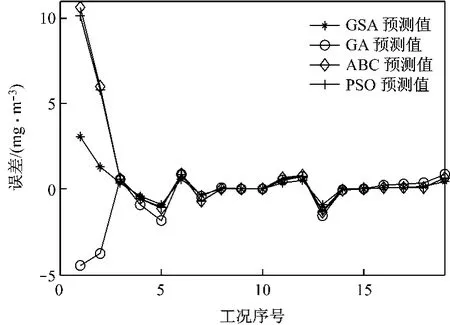
图5 各算法预测值与实测值之间的误差Fig.5 Curves of error between predicted values by various algorithms and actual measurements

表3 预测数据准确度的比较Tab.3 The accuracy comparison of test data

4 结束语

以某330MW煤粉汽包锅炉为测试对象，阐述了GSA搜索算法与LSSVR综合建模的方法.首先，利用LSSVR建立了电站锅炉燃烧系统模型并得到了锅炉燃烧系统中NOx质量浓度的预测模型；然后，利用GSA搜索算法寻找最优化参数；最后，将GSA搜索算法与另外3种智能算法进行了对比仿真.仿真结果表明，GSA算法比以往采用的智能算法具有更好的准确性和较强的泛化能力，从而可有效控制燃煤电厂NOx的排放、实现低污染.

［1］王培红，李磊磊，陈强，等.人工智能技术在电站锅炉燃烧优化中的应用研究［J］.中国电机工程学报，2004，24（4）：184－188.WANG Peihong，LI Leilei，CHEN Qiang，et al.Research on applications of artificial intelligence to combustion optimization in a coal－fired boiler［J］.Proceedings of the CSEE，2004，24 （4）：184－188.

［2］刘定平，陈敏生，陆继东，等.电站锅炉高效低污染燃烧优化控制系统设计［J］.电力自动化设备，2006，26（5）：46－49.LIU Dingping，CHEN Minsheng，LU Jidong，et al.Optimized control system design for high efficiency and low emission combustion of power plant boiler［J］.Electric Power Automation Equipment，2006，26（5）：46－49.

［3］魏辉，陆方，罗永浩，等.燃煤锅炉高效、低NOx运行策略的研究［J］.动力工程，2008，28（3）：361－366.WEI Hui，LU Fang，LUO Yonghao，et al.Research on operation strategy on reducing NOxemissions and improving efficiency of coal－fired boiler［J］.Journal of Power Engineering，2008，28（3）：361－366.

［4］RASHEDI Esmat，NEZANUDMDI－POUR Hossein，SARYAZDI Saeid.GSA：agravitational search algorithm［J］.Information Sciences，2009，179（13）：2232－2248.

［5］邓乃扬，田英杰.数据挖掘中的新方法——支持向量机［M］.北京：科学出版社，2004.

［6］赵欢，王培红，陆璐，等.电站锅炉热效率与NOx排放响应特性建模方法［J］.中国电机工程学报，2008，28（32）：96－100.ZHAO Huan，WANG Peihong，LU Lu，et al.Response characteristics modeling of efficiency and NOxemission for power station boiler［J］.Proceedings of the CSEE，2008，28（32）：96－100.

［7］阎威武，邵惠鹤.支持向量机和最小二乘支持向量机的比较及应用研究［J］.控制与决策，2003，18（3）：358－360.YAN Weiwu，SHAO Huihe.Application of support vector machines and least squares support vector machines to heart disease diagnoses［J］.Contorl and Decision，2003，18（3）：358－360.

［8］郑立刚，周昊，王春林，等.变尺度混沌蚁群算法在NOx排放优化中的应用［J］.中国电机工程学报，2008，28（11）：18－23.ZHENG Ligang，ZHOU Hao，WANG Chunlin，et al.Application of scaleable chaotic ant colony algorithm in NOxemissions optimization［J］.Proceedings of the CSEE，2008，28（11）：18－23.

［9］KEERTHI S，LIN C J.Asymptotic behaviors of support vector machines with Gaussian kernel［J］.Neural Computation，2003，15（7）：1667－1689.

［10］MANSOURI R，NASSERI F，KHORRAMI M.Effective time variation of G in a model universe with variable space dimension［J］.Physics Letters，1999，259（3／4）：194－200.

［11］王春林，周昊，周樟华，等.基于支持向量机的大型电厂锅炉飞灰含碳量建模［J］.中国电机工程学报，2005，25（20）：72－77.WANG Chunlin，ZHOU Hao，ZHOU Zhanghua，et al.Support vector machine modeling on the unburned carbon in fly ash［J］.Proceedings of the CSEE，2005，25（20）：72－77.