火箭助飞鱼雷飞行可靠性评定方法

孙公道，尹文进，林一品

(1. 91550 部队，辽宁 大连 116023;2.海军工程大学，武汉 430033;3. 92858 部队，浙江 宁波 315812)

鉴于现代战争远距离作战的特点，作为一种中远距离打击武器，火箭助飞鱼雷在现代海战中的地位也日益提升。现代海战的发展使其对武器的可靠性要求也与日俱增。火箭助飞鱼雷飞行阶段可靠性评估，是该武器靶场试验内容的一个重要方面。由于研制成本的限制和研制时间的要求，难以投入大批量的样本进行试验。在小样本情况下，如何对火箭助飞鱼雷飞行可靠性进行准确评估就成为火箭助飞鱼雷定型鉴定中的一大难题。

1 飞行可靠性评定的特点

1)系统的整机试验次数较少且技术状态比较复杂。由于使用操雷进行试验之后，可以将其回收重复利用，因此舰用和潜用鱼雷在进行可靠性试验时，常使用操雷代替战雷。因此，就可以在较大的样本空间中对舰用(或潜用)鱼雷进行可靠性评定。而火箭助飞鱼雷的特点决定其无法用操雷代替，导致一次试验的代价较为昂贵，因此难以投入大量的样本空间进行试验。为降低试验成本，往往把多个指标的验证工作放在一枚火箭助飞鱼雷的试验中去。这就使得火箭助飞鱼雷的技术状态复杂化，增加了指标评定的难度。

2)飞行试验分阶段进行。火箭助飞鱼雷的飞行试验是一个纷繁复杂的过程，需要根据不同的试验目的而分阶段进行的。由于不同阶段的试验目的各不相同，因此火箭助飞鱼雷在每一试验阶段的技术状态也不尽相同。一般情况下，在研制性飞行试验结束之后，火箭助飞鱼雷的技术状态基本上不会发生较大的变化。为充分发掘研制阶段试验数据的作用，在定型飞行试验阶段，就可以充分利用研制期间所得到的试验数据对火箭助飞鱼雷的飞行可靠性指标进行评定。

2 飞行可靠性的验前信息

将火箭助飞鱼雷地面试验数据与飞行试验数据进行综合，就需要对验前信息的获取的途径和方法进行总结，并研究试验数据的转换方法。将火箭助飞鱼雷系统或其分系统可靠性看作为成败型数据还是指数型数据，则需要进一步的探索和研究。

通过试验，得到火箭助飞鱼雷飞行可靠性验前信息，如何对其进行处理，是我们面临的又一问题。本文的处理方法如下:首先使用天地环境因子将火箭助飞鱼雷分系统的地面试验数据折算为飞行可靠性数据，其次折算火箭助飞鱼雷分系统飞行试验数据，将其折算为标准射程下的飞行可靠性数据。最后将上述结果进行一定的系统综合，从而能够得到火箭助飞鱼雷飞行可靠性验前信息。流程图如图1 所示。

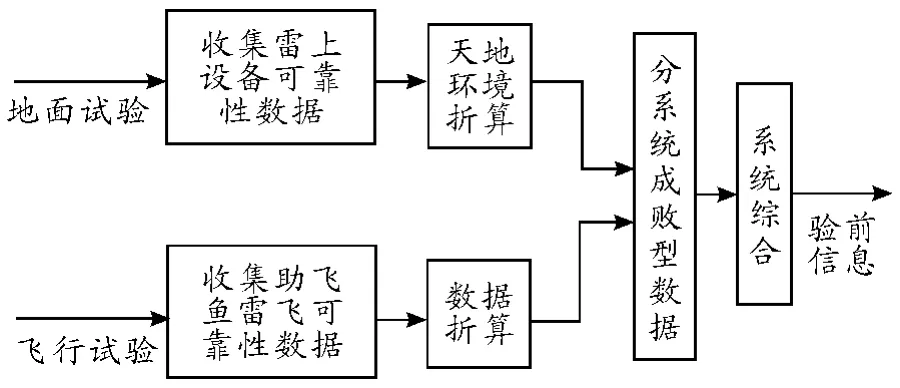
图1 验前信息处理流程

2.1 获取飞行可靠性验前信息的途径和方法

1)单元和分系统的试验信息:由于进行系统级试验的代价过高，我们可以采用其他方法来避免大量的系统级试验。而单元和分系统的试验成本往往较为低廉，针对这一特点，我们使用“金字塔”式的评定方法［1］，即对系统进行少量试验，而对分系统和单元进行大量试验。这样，降低了整体试验成本。

2)仿真试验信息:近年来，随着仿真技术在工程上的应用越来越广泛，可靠性仿真也逐渐成为一种新兴的可靠性技术。通过可靠性仿真试验，可以为火箭助飞鱼雷武器系统的可靠性评估提供验前信息，减少了靶场试验的任务量，使试验成本大大降低。

3)相似系统的信息:由于新型号武器系统同旧的型号武器系统之间往往有很多继承性，有些型号改进很小，充分合理地利用这些信息可以有效减少试验次数。

4)不同环境下的系统试验信息:火箭助飞鱼雷的可靠性与其所处的环境息息相关。因此，我们对验前信息进行处理时，应考虑到一点:该验前信息是在何种环境条件下获取的。根据不同环境下试验信息进行折算的前提要求为:武器系统的失效机理或各组成单元不变。使用这种信息时需要考虑到环境因子折算问题。

5)专家意见及工程经验:在对火箭助飞鱼雷武器系统进行可靠性评估时，专家意见或工程经验也可以作为一种可以利用的验前信息。

6)可靠性增长信息:主要是历史信息，包括单元或系统在不同的试验阶段下得到的试验信息。

2.2 地面试验数据综合为飞行试验数据

为提高结果的可信度，需充分利用不同环境下的试验数据，即将不同环境下的试验数据进行综合。进行数据综合是这样一个过程:首先把不同环境下得到的试验数据折算到同一环境下，然后。在同一环境下进行综合［2］。为此，应计算出不同环境之间的环境因子;其次，折算环境因子;最后，综合试验数据［3］。

2.2.1 环境因子的确定

飞行试验结果为(s1，f1)，地面试验结果为(s2，f2)，si、fi(i=1，2)分别为二者的成功次数和失败次数。当置信度为γ时，Ri的概率密度为:

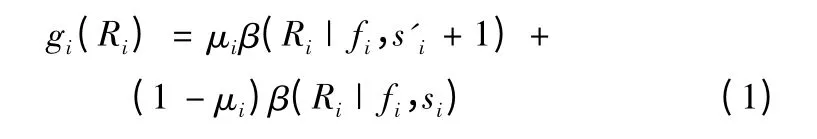
K=R1/R2概率密度为

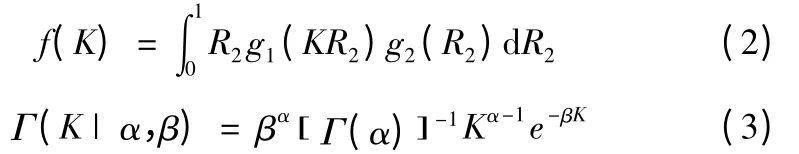
用式(3)作为近似分布用以拟合K 的精确概率密度，拟合的条件是Г(K|α，β)的一、二阶矩相等。Г(K|α，β)的一、二阶矩分别为:α/β，α(α +1)/β。记K 的一、二阶精确分布的矩分别为:μ≈EK，ν≈EK2。定义Kμ的近似值~Kμ，~Kμ满足式(4)

因此

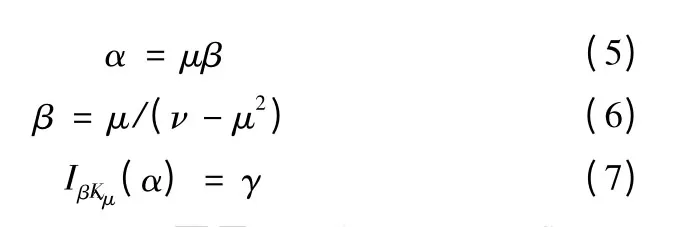
其中:Ix(α)是不完全Г 函数，可用式(8)、式(9)求得μ、ν的值

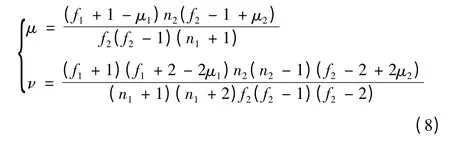
成败型数据的特性决定了其计算过程往往过于繁杂。为降低计算量，需将纷繁复杂的成败型数据转换成易于计算的指数型数据，但首先要根据指数型产品环境因子对数据进行折算。

2.2.2 环境因子折算

对火箭助飞鱼雷飞行可靠性进行评估，通常考核的是火箭助飞鱼雷在飞行环境条件下其可靠性所能够达到的程度，因此需要使用环境因子折合地面环境下的试验数据，以便在统一在同一飞行环境下进行评估。根据给定置信度γ，求得置信上限Kμ(环境因子)，根据环境因子将地面试验数据转换为飞行试验数据。即:将数据(n2，f2)转换为数据(n2/Kμ，f2)，ni(i=1，2)为试验数。

2.2.3 综合不同环境下试验数据

根据式(10)综合飞行试验数据N11，F11(N11是试验数，F11是失败数)

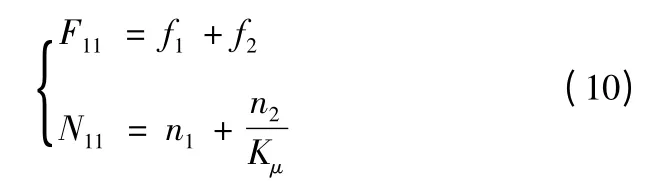
通过上式求得N11，F11后，可以进一步求得飞行条件下的可靠性下限RLB。

2.3 数据类型转换

在对验前信息的处理过程中，将不可避免地会遇到试验数据转换的问题。试验数据转换不仅仅是指数型数据转换为成败型数据，而且还包含成败型数据转换为指数型数据问题，可以采用贝叶斯法和经典法对其进行转换［4］。

2.3.1 贝叶斯法

1)指数型数据转换为成败型数据

若已知条件为:任务时间t，指数型数据为(Z，η)，可根据式(11)、式(12)来确定n 和f:

当Z≠0 时

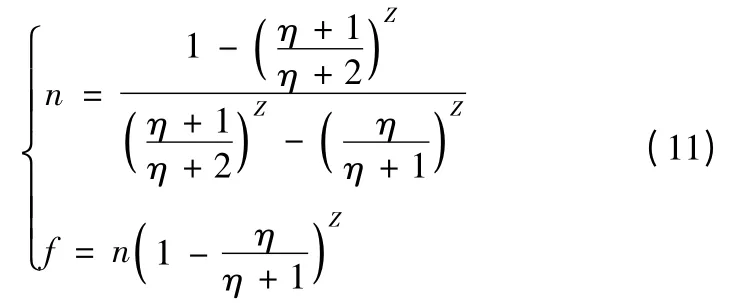
当Z=0 时

2)成败型数据转换为指数型数据

已知条件为:试验结果数据(n，s)，则η，Z 可由式(11)、式(12)确定:

当f≠0 时

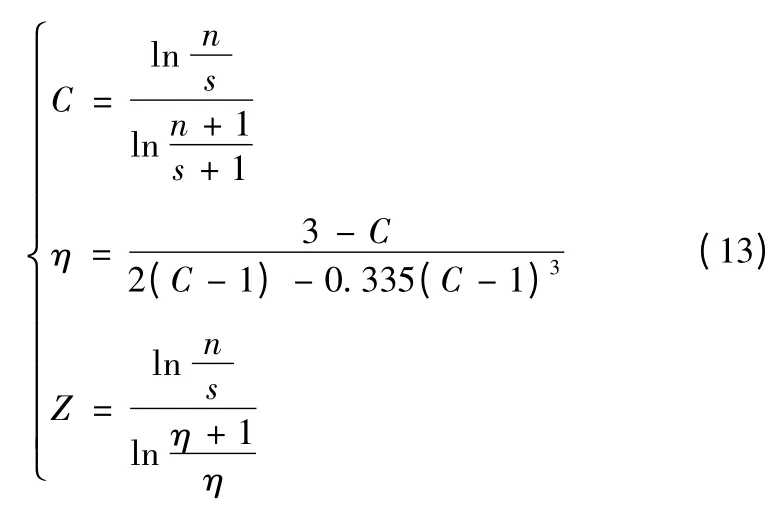
当f=0 时

2.3.2 经典法

1)指数型试验数据转换为成败型数据

已知试验数据为(Z，η)时，则n、f 根据式(15)、式(16)来确定:

当Z≠0 时

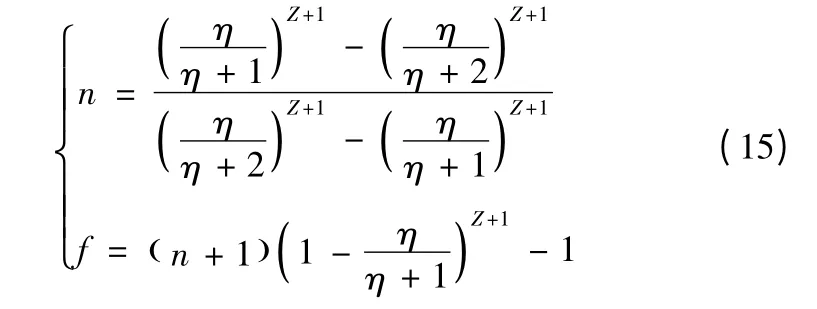
当Z=0 时

2)成败型数据转换为指数型数据

已知试验数据为(n，s)，η，Z 可由式(17)、式(18)确定:当f≠0 时

当f=0 时

2.4 综合分系统数据为系统数据

将各分系统(或单元)全都转换为成败型分系统(或单元)后，就可以通过矩匹配法将它们折合为成败型系统［5］。

2.4.1 串联系统

假定有m 个成败型单元构成串联系统，记:Ri，ni分别为第i 单元的可靠性和试验次数，si为第i 单元在ni次试验中的成功次数，则可以用式(19)来表示该串联系统的可靠性

当Ri之间互相独立时 可以根据 规则 选取验前密度

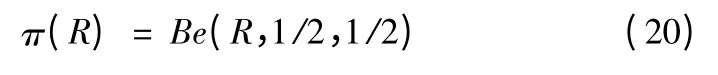
有

这样就确定了等效系统，其中(n，f)为串联系统的等效系统特征。

2.4.2 并联系统

设n 个独立成败型分系统(或单元)并联成系统，记:Rj和Qj=1 -Rj分别为第j 单元的可靠性与不可靠性;fj为第j单元在nj次试验中的失败次数，那么可以根据式(25)来确定并联系统的可靠性R

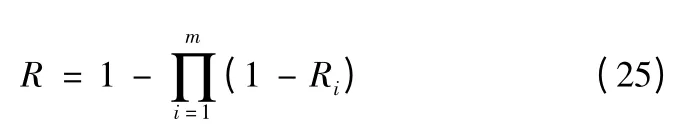
或

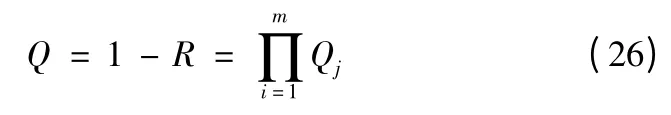
那么，并联系统的可靠性处理就有了新的解决方案:可以转化为串联系统的不可靠性来进行处理。选取验前密度为

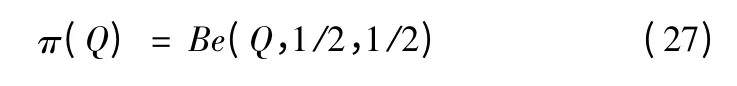
有

记并联系统折合特征为(n，s)，那么有:

3 可靠性评定方法

可靠性评定是这样一个过程:进行可靠性试验，通过试验获得有限样本数，对各个可靠性指标可能会达到的下限(上限)进行评定。由于采用的样本信息是有限样本信息，因此所得到的是一定置信度条件下的评定结论。即在给定置信度γ 的条件下，对于可靠度R，满足公式P(R≥RL)≥γ 的下限值RL，称其为满足给定置信度γ 下的可靠性置信下限。可靠性评定作为评估火箭助飞鱼雷武器系统作战效能的一个重要方面，一般较为常用的评定方法有经典法和贝叶斯法［2］。

3.1 经典法

通过定型试验，可以得到一定的样本信息。经典法根据得到的样本信息对定型批火箭助飞鱼雷的飞行可靠度进行统计和推断。在火箭助飞鱼雷武器系统定型试验阶段，主要目的是验证火箭助飞鱼雷在飞行环境中的飞行可靠度。因此在定型试验阶段，主要进行火箭助飞鱼雷的飞行试验。

试验结果为(n，s)，其中n 是试验次数，s 为试验中的成功数，那么试验中的失败数为f=n-s。

1)点估计

无论是采用极大似然估计法还是使用矩估计法，R 的估计量均为

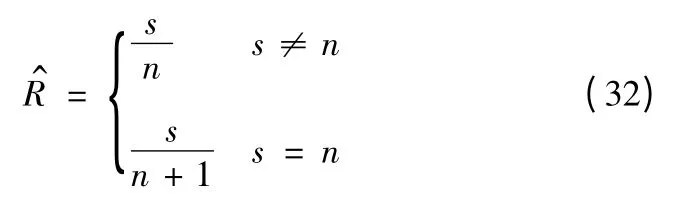
2)区间估计

在置信度为γ 的条件下，根据不完全β 函数可以表示可靠性的下限RLC

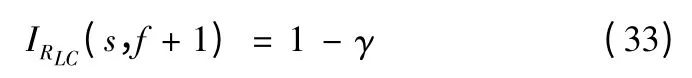
给定置信度为γ，根据n，f 查二项分布表即可得到RLC。

3.2 贝叶斯法

设系统可靠性服从β 分布，验前分布密度为β(R|s0，f0)，式中s0为验前成功数，f0为验前失败数，则其验前试验数为n0=s0+f0，经过n 次试验，试验结果记为(n，s)，则其验后分布为β(R|s+s0，f+f0)。

3.2.1 点估计

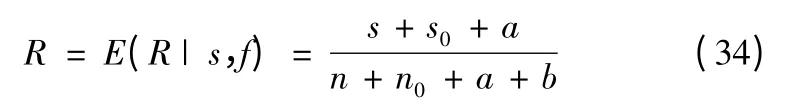
设定a=b=0.5，则其贝叶斯估计为:

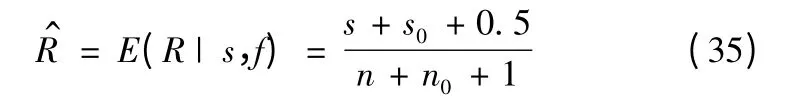
3.2.2 区间估计

在给定置信度为γ 时，可以通过式(36)来确定可靠性下限RLB

在工程应用中，不根据式(36)进行计算，而是根据给定置信度γ，查二项分布表求出RLB。

4 案例分析

根据本文所提供的贝叶斯法和经典法，结合每个试验阶段所得到的试验数据，评定火箭助飞鱼雷的飞行可靠性。在产品的定型试验阶段，共计发射9 枚火箭助飞鱼雷，其中8发试验成功。根据上述实例，对火箭助飞鱼雷飞行可靠性进行评定，结果如下。

4.1 经典法

根据式(32)，采用点估计的方法，可计算得到飞行可靠性点估计值=0.888 9;通过式(33)进行计算，可以得到飞行可靠性的下限=0.702 23。

4.2 贝叶斯法

4.2.1 数据转换

将分系统的指数型数据转换成为成败型数据，转换结果如表1 所示。

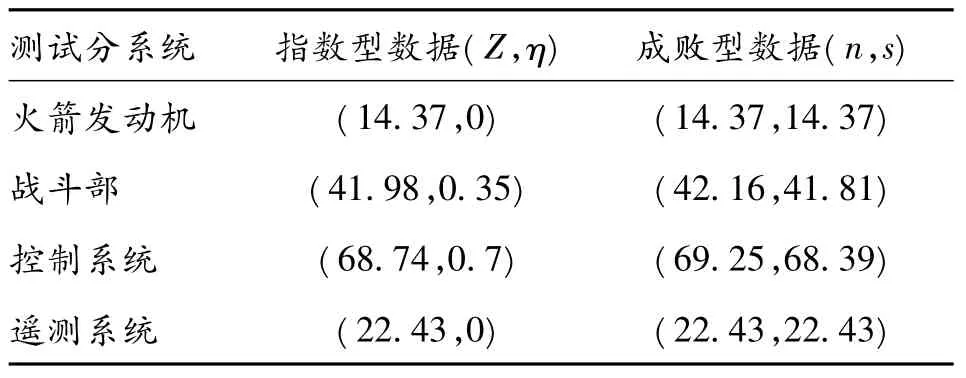
表1 地面试验数据转换结果

鉴于火箭助飞鱼雷系统中存在着零失效单元，因此可以采用经典法对转换后的数据进行融合。计算结果为

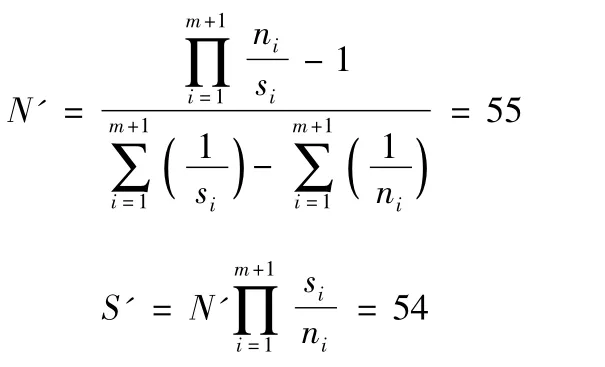
4.2.2 计算环境因子

研制阶段共发射火箭助飞鱼雷9 枚，7 枚发射成功，根据此例，进行计算。研制阶段火箭助飞鱼雷的飞行试验数据为整理地面试验数据后，得通过式(8)计算得β =0.1267，α =0.3857。取γ =0.8，通过公式(9)计算得到研制阶段的环境因子为~Kμ=1.6。

4.2.3 系统数据综合

将研制阶段试验数据综合为飞行试验环境下的数据，根据式(10)计算能够得到数据把地面试验数据作为验前信息，可以得到火箭助飞鱼雷可靠性验前信息在定型试验阶段，火箭助飞鱼雷的飞行可靠性数据为

5 结束语

通过上文可以得知，在同一置信度条件下，相比于使用经典法计算所得到的点估计值和估计下限，采用贝叶斯法所处理的结果更为合理一些。这是因为经过各阶段多次试验后，工程技术人员都会针对试验中出现的问题进行改进，产品的可靠度也必将会有所提升。经典法没有将历次试验所得到的信息作为考虑因素，而仅仅使用改进后设备的试验信息。因此，根据经典法计算得到的评估结论往往偏于保守。而贝叶斯法的优势在于能够充分综合利用各个阶段的全部数据，使样本量能够得到扩大。以信息论的观点来看，采用贝叶斯法所得到的计算结果更为合理，也更具有说服力。

［1］程德斌.导弹飞行可靠度评定方法初探［J］.系统与装备可靠性，2005(12):85-88.

［2］金振中，李守秀，甄昕.反舰导弹飞行可靠性验前信息分析与综合［J］.质量与可靠性，2000(3):26-28.

［3］郭梅忠.地地战术导弹飞行可靠性指标评定方法［J］.战术导弹技术，2002，7(4):12-16.

［4］吴建业.反舰导弹飞行可靠性评估方法研究［D］.长沙:国防科技大学，2009.

［5］刘智洋.利用设备变母体变环境数据的系统可靠性综合评估［J］. 北京航空航天大学学报，2004，29( 8): 254-257.