基于CFX的磨料水射流喷嘴的流场分析
刘巨保,徐世博,娄永
(1.东北石油大学机械科学与工程学院,黑龙江大庆 163318;2.大庆油田有限责任公司井下作业分公司,黑龙江大庆 164325)①
磨料水射流是近年来发展起来的新技术,它是由一定尺寸的磨料与水相互混合成具有一定比例的固液两相射流[1]。射流喷嘴是将高压液体的能量转化为混合流体的动能,它决定了切割液在通过喷嘴后的流场的动力特性和分布特性,是整个射流设备的核心部件之一。因此,研究射流喷嘴结构对流场影响具有重要意义。
磨料水射流是多相混合的介质射流,其机理十分复杂,简单的理论研究无法对喷嘴内部及射流的流场进行真实的描述。由于流场扰动和现阶段的技术手段和测量方法精确性的限制,又无法通过实验获得理想的结果。仿真模拟可以克服理论方法和实验的不足[2],即通过计算就可以模拟整个流场的速度、压力等相应的结果,相对其他方法具有准确、可靠、方便等优点。国内外专家在射流喷嘴的数值模拟方面做了许多的研究,黄志强[3]等利用Fluent对井底流场进行了数值模拟,研究了喷嘴直径与井底流场的关系。郭仁宁[4]等对射流喷嘴内的流场进行了数值模拟,研究了喷嘴混合腔内的流动与喷嘴结构的关系,为喷嘴寿命的设计提供了理论依据。杨国来[5]等研究了空化射流喷嘴内边界层及其稳定性之间的关系。王东[6]等通过分析得到了射流切断面积和材料破坏能量关系的曲线。Babets[7]等对喷嘴进行了数值模拟,得出喷嘴结构对流体分离和空化的影响。Flowler[8]等对流体切割参数对切割效果的影响做了相应的研究分析。本文比较分析了2种喷嘴的流场,为射流切割工艺选择合适的喷嘴提供参考。
1 模型建立与离散
本文主要研究喷嘴在淹没射流条件下的流动特性。因为在射流过程中固相所占比例较大,所以选用欧拉模型进行模拟。对不同结构的喷嘴建立相应的实体网格模型,如图1所示。喷嘴直径为2mm,喷出段长度为80mm,喷出段直径为30mm,模型角度为10°。
图1 锥形喷嘴模型的有限元网格
2 边界条件设定
入口边界条件:入口采用速度边界。流体为两相混合液体,磨料的体积分数为12%,粒径为0.5 mm,密度为2300kg/m3,黏度为1×10-9Pa·s。水的体积分数为88%。采用标准的k-ε模型进行模拟。
标准k-ε数学模型为:
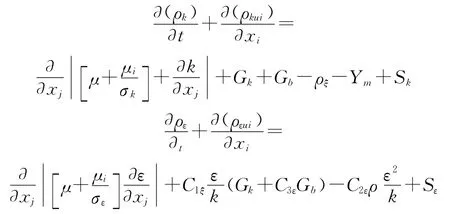
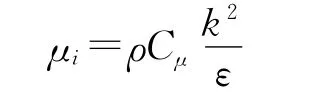
在CFX 中,C1ε=1.44,C2ε=1.92,C3ε=0.09为经验常数,湍流能k 与湍流耗散率ε的湍流普朗特数分别为σk=1.0,σε=1.3[2]。
3 流场仿真结果分析
3.1 锥形喷嘴的压力和速度分布
本文首先对锥形喷嘴进行了数值模拟,喷嘴长度为8mm,出口直径为2mm,入口直径为4mm,锥度为1∶2。其压力分布云图如图2所示,从图中可知,由于高压流体射入低压流体,使低压流体区形成负压,通过高压流体的喷射不断带出,保证低压介质的不断流出,从而使得喷嘴出口处的压力小于环境的相对压力。喷嘴的流场速度分布如图3~4所示。

图2 锥形喷嘴的压力分布云图

图3 锥形喷嘴固相速度分布云图

图4 锥形喷嘴液相速度分布云图
从图2~4可以看出,液相和固相在喷嘴内被加速,流体的压能转换为两相的动能,当液相从喷嘴中喷出时速度达到最大,而固相在喷出后一段距离才能达到最大。无论是液体相还是固体相都由初始段与主体段2个部分组成,其中初始段速度较大,正是磨料射流切割需要的部分,在这个部分中,混合液具有较大速度和较好的集束性,能级密度较大,切割效果最佳。图5为中心轴线处两相速度分布。从图5可以看出,液相最高速度209m/s,出现在距喷嘴出口0.002m 处,然后随距喷嘴出口距离的增大而减小,达到0.013m 处进入主体段后,速度急剧下降。固相最高速度发生在距喷嘴出口0.008 m 处,为174.3m/s,进入主体段内后速度急剧下降。说明固相在从喷嘴喷出后,由于在喷嘴内未充分加速,液相速度大于固相速度,进而导致在初始段固相依然被液相部分所加速,从而导致该种现象的发生。
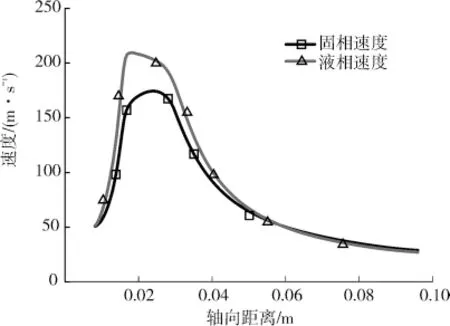
图5 锥形喷嘴液相速度分布云图
3.2 不同锥度锥形喷嘴中心轴线处的速度分布
图6~7为不同锥度喷嘴中心轴线处速度分布,表1为不同锥度的计算数据。从表1和图6可以看出随着喷嘴锥度的增加,固相喷出后的最大速度逐渐降低,由174.3m/s下降到159.0m/s,最大速度发生点距喷嘴出口的距离逐渐缩短,固相在初始段内速度波动降低,稳定段增长。从图7和表1中还可以看出,随喷嘴锥度的增加,液相几乎在距喷嘴同一位置处达到最大值,最大值稍有减少(由209.5 m/s下降到203.7m/s)。在达到最大流速后,液相在初始段的流速衰减速率随锥度的增大而增加,这也解释了为什么固相颗粒在初始段内速度随锥度的增加而波动降低,稳定段增长。
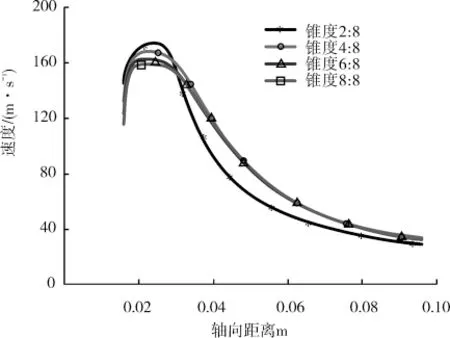
图6 不同锥度固相速度分布云图

图7 不同锥度液相速度分布云图
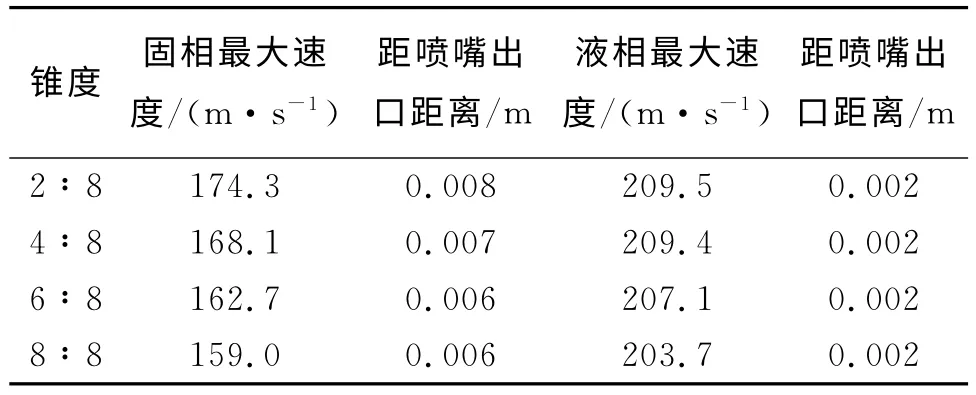
表1 不同锥度计算数据
3.3 锥直形喷嘴的压力和速度分布
因为磨料射流切割主要依靠磨料颗粒以极高的速度撞击金属表面侵入破坏,从而实现射流切割。因此磨料颗粒的速度是射流喷嘴结构设计的主要目标之一,所以对于锥形喷嘴来说固相颗粒并没有在喷嘴中充分的被加速,应该设法提高固相颗粒的速度,这样才能充分利用流体的能量,达到切削效果。本文研究了另外一种锥直形喷嘴,即在锥形喷嘴的基础上在出口段加入一段直管段。建立了锥直形喷嘴的实体模型,其网格模型如图8所示,锥管段的长度为8mm,锥度为6∶8,其余边界条件与锥形喷嘴相同。

图8 锥直形喷嘴网格
锥直形喷嘴的压力分布如图9所示。从图9中可以看出喷嘴入口压力较高,当混合液流经喷嘴后压力降低,压能转换为混合液的动能。但同时发现整体压力分布中存在负压,将负压位置局部放大,如图10所示。从图10中可以看出,负压区发生在锥管段结束,进入直管段处,这是因为混合液在直管处产生收缩,而混合液在流出之前又充满了直管段的截面,因为计算边界的参考压力为0.1MPa,所以在直管的初始段处出现负压。由于负压的产生,使得直管初始段能够抽吸前段的混合液,对于射流切割来讲是有益的。但这个负压不应小于当地的饱和蒸汽压力,否则当液相流经该截面时会发生汽化。

图9 锥直形喷嘴压力分布云图

图10 锥直形喷嘴压力局部放大云图
3.4 不同直管段长度的锥直形喷嘴中心轴线处速度分布
图11~12为不同直管段长度固液两相的轴线位置喷射速度。具体数据如表2。从图11和表2可以看出,当锥管段确定,随着直管段的加长,固体颗粒的速度逐渐增大,颗粒最大速度出现点离喷嘴出口距离大致相同,固相初始段的长度变化不大。从图12和表2可以看出,随着直管段的增长,液相的出口速度逐渐的降低,并且在初始段内速度的衰减速率逐渐降低。因此延长直管段的长度,能够提供更加稳定的喷射流场。由表2第2列可以看出,随着直管段增加,可以明显改善由于收缩断面上产生的负压,对于以水为液相的高速射流,可防止局部水的相变。对比表2和表1中的数据可知,固体颗粒在两种喷嘴的加速条件下,锥直形的喷嘴固相颗粒的速度为180m/s,而锥形喷嘴为160m/s,这说明锥直形喷嘴可以使固相颗粒更好地被加速,以达到更高的速度。
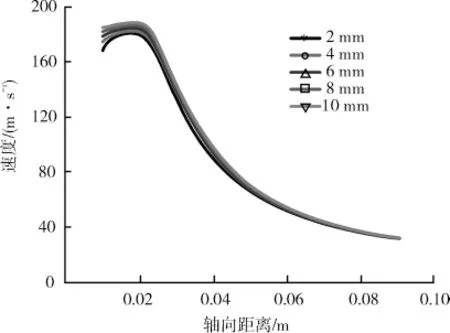
图11 不同直管段长度固相速度分布
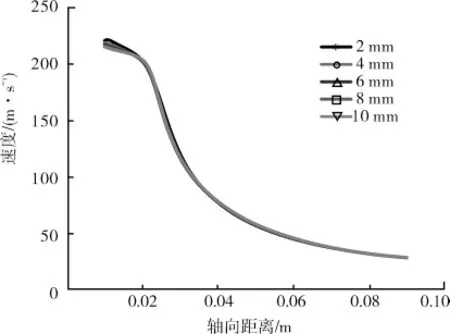
图12 不同直管段长度液相速度分布

表2 不同直管段计算数据
4 结论
1)采用CFX 对喷嘴进行了两相流的数值模拟,仿真的结果与理论的结果基本吻合。分别对锥形喷嘴和锥直形喷嘴进行了计算,得到了两种不同形状喷嘴流场分布,其中锥直形喷嘴的固相颗粒速度比锥形喷嘴的更高,更适合磨料射流切割。
2)对于锥形喷嘴,在喷嘴长度不变的情况下,增加锥度会使混合液内的固相和液相的喷出速度降低,对于磨料射流切割,如果选用此种喷嘴应在可能的情况下尽量减小锥度,以达到更高的固相速度,提高效率。
3)对于锥直形喷嘴,适当增加直管段的长度,能够增加固相颗粒的速度,并降低在缩颈断面上产生的负压,并且能够使得混合液的液相在喷嘴外的初始段内具有较好的稳定性,这同样有利于磨料射流切割。
[1]李根生,黄忠伟,田守嶒,等.水力喷射压裂理论与应用[M].北京:科学出版社,2011.
[2]王福军.计算流体动力学分析-CFD 软件原理与应用[M].北京:清华大学出版社,2004.
[3]黄志强,周已,李勤,等.刮刀钻头喷嘴直径对井底流场的影响研究[J].石油矿场机械,2009,38(3):17-19.
[4]郭仁宁,王若旭,陈扬.磨料水射流喷嘴的流场数值模拟[J].化工进展,2009,28:443-446.
[5]杨国来,周文会,刘肥.基于Fluent的高压水射流喷嘴的流场仿真[J].兰州理工大学学报,2008,34(2):48-52.
[6]王东,吴雨川,罗维平,等.高压水射流切割流场的数值模拟研究[J].武汉科技学院学报,2005,18(3):15-18.
[7]Babets K E,Geskin.Numerical study of the turbulent flow inside a pure water jet[C].Proc 11th U S Water Jet Conference,2001.
[8]Flower G,sgipway p h,pashby I R.A technical note on grit embedment fllowing abrasive water-jet milling of a titanjum alloy[J].Journal of material processing Technology,2005,159(5):256-368.

