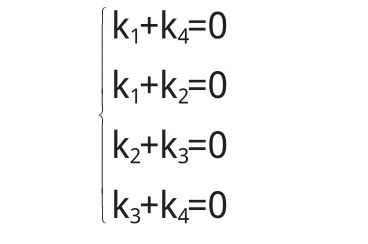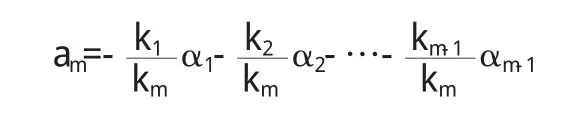判断向量组线性相关性的常用方法
梁玥
(甘肃农业大学 理学院,甘肃 兰州 730070)
判断向量组线性相关性的常用方法
梁玥
(甘肃农业大学 理学院,甘肃 兰州 730070)
从向量组中各向量的分量是否具体给出的角度出发,归纳了判断向量组线性相关性的几种常用方法.
向量组;分量;线性相关;线性无关;判定方法
向量组的线性相关性在数学领域中有着非常重要的作用,它与行列式、矩阵、线性方程组的解、二次型、线性变换以及欧氏空间都有着重要的联系.然而向量的线性相关与线性无关的判别是比较抽象和难理解的.实际上,向量组的线性相关与线性无关是相对的,我们只要掌握了线性相关的判别,那么线性无关的判别也就迎刃而解了.下面根据向量组中各向量的分量是否具体给出介绍向量组线性相关性的判别方法.
1 分量给出的向量组线性相关的判断
1.1利用齐次线性方程组的解判断
若α1,α2,…,αm为系数向量的齐次线性方程组有非零解,则向量组α1,α2,…,αm线性相关;若该齐次线性方程组只有零解,则向量组α1,α2,…,αm线性无关.
1.2利用矩阵的秩判断
以α1,α2,…,αm作为列向量构成矩阵A=(α1,α2,…,αm),对矩阵施行初等行变换化为行阶梯形矩阵,由此求出矩阵A的秩R(A):
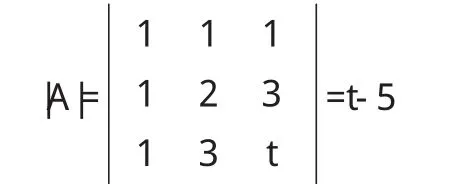
(1)当R(A) (2)当R(A)=m时,向量组α1,α2,…,αm线性无关. 1.3利用行列式的值判断 若向量组α1,α2,…,αm的个数等于向量的维数,则以α1,α2,…,αm作为列向量构成的矩阵A=(α1,α2,…,αm)是一个方阵,而方阵可以取行列式: (1)当|A|=0时,向量组α1,α2,…,αm线性相关; (2)当|A|≠时,向量组α1,α2,…,αm线性无关. 解 以α1,α2,α3为系数向量的齐次线性方程组是 利用矩阵的初等行变换将方程组的系数矩阵A化为行阶梯形矩阵 由行阶梯形矩阵知,R(A)=2<3,即该齐次线性方程组有非零解,所以向量组α1,α2,α3线性相关. 解法1 以α1,α2,α3为列向量构成的矩阵为 A=(α1,α2,α3) 可见,当t=5时,R(A)=2<3,所以向量组α1,α2,α3线性相关. 解法2 向量组α1,α2,α3的个数和维数相等,都为3,由1.3节的方法有 可见当t=5时,|A|=0,所以向量组α1,α2,α3线性相关. 用1.1,1.2和1.3进行判断的出发点不同,但实质是一样的.1.1和1.2都是要利用矩阵的初等行变换将相应的系数矩阵化简为行阶梯形矩阵,从而求出向量组的秩即系数矩阵的秩,然后再作出判定.而1.3是根据克莱姆法则判别以向量组各向量作为系数向量的齐次线性方程组有无非零解,然后对向量组的线性相关性做出判定,所以可用1.3进行判定时也可用1.1和1.2进行判定. 2.1定义法 这是判断向量组线性相关性的基本方法. 其定义是:给定向量组A:α1,α2,…,αm,如果存在不全为零的数k1,k2,…,km,使得k1α1+k2α2+…+kmαm=O,则称向量组A是线性相关的.否则称它是线性无关的,也就是说当且仅当k1,k2,…,km全部为零时才成立,则称向量组A是线性无关的. 例3 设β1=α1+α2,β2=α2+α3,β3=α3+α4,β4=α4+α1,证明β1,β2,β3,β4线性相关. 证明 设有数k1,k2,k3,k4,使即 k1(α1+α2)+k2(α2+α3)+k3(α3+α4)+k4(α4+α1)=O亦即(k1+k4)α1+(k1+k2)α2+(k2+k3)α3+(k3+k4)α4=O (1)若向量组α1,α2,α3,α4线性相关,则由上式可知,k1+k4,k1+k2,k2+k3,k3+k4不全为零,故k1,k2,k3,k4不全为零(否则,k1+k4,k1+k2,k2+k3,k3+k4全为零),所以向量组β1,β2,β3,β4线性相关. (2)若向量组α1,α2,α3,α4线性无关,则有 2.2用向量组的秩判断 向量组的秩是指向量组中任一个极大无关组所含的向量个数.设向量组为A:α1,α2,…,αm,其秩记为R(α1,α2,…,αm),由极大无关组的定义和秩的定义可得:若向量组的秩等于向量的个数,则该向量组是线性无关的;若向量组的秩小于向量的个数,则该向量组是线性相关的.(例略) 2.3用线性相关性的常用定理判断 定理1 向量组A:α1,α2,…,αm(m≥2)线性相关⇔向量组Aα1,α2,…,αm中至少有一个向量可以由其余的m-1个向量线性表示. 定理2 向量组A:α1,α2,…,αm线性无关,而向量组B: α1,α2,…,αm,β线性相关⇒β可由向量组A:α1,α2,…,αm线性表示且表达方式唯一. 定理3 若向量组A:α1,α2,…,αm有一部分向量组线性相关⇒向量组A:α1,α2,…,αm线性相关.与此等价的一个说法为:向量组A:α1,α2,…,αm线性无关⇒向量组A:α1,α2,…,αm的任一部分向量组线性无关. 例4 已知α1,α2,α3线性无关,α2,α3,α4线性相关,问: (1)α4能否由α1,α2,α3线性表示? (2)α1能否由α2,α3,α4线性表示? 解 (1)由α1,α2,α3线性无关⇒α2,α3线性无关,又由α2,α3,α4线性相关⇒α4能由α2,α3线性表示且表达式唯一,所以存在数k2,k3,使得,故α4能由α1,α2,α3线性表示. (2)反证法.假设α1能由α2,α3,α4线性表示,则存在数又由(1)α4能由α2,α3线性表示,所以α1能由α2,α3线性表示,所以α1,α2,α3线性相关,与已知矛盾,故α1不能由α2,α3,α4线性表示. 2.4用反证法 在有些题目中,直接证明结论有时候比较困难,而从结论的反面入手却很容易推出一些与已知条件或已知定义、定理、公理相矛盾的结果,从而结论的反面不成立,则结论成立. 例5 设向量组α1,α2,…,αm中任一向量αi不是它前面i-1向量的线性组合,且αi≠0,证明向量组α1,α2,…,αm线性无关. 证明 (反证法)假设向量组α1,α2,…,αm线性相关,则存在不全为零的数k1,k2,…,km,使得: 由此可知km≠0,由上式可得 即αm可以由它前面m-1个向量线性表示,这与题设矛盾,因此km=0于是(1)式转化为k1α1+k2α2+…+km-1αm-1=0.类似于上面的证明可得km-1=km-2=…=k2=0,(1)式转第为k1α1=0,但α1≠0,所以k1=0这与k1,k2,…,km不全为零的假设相矛盾,因此向量组线性无关. 以上从向量组的分量是否具体给出两个大的方面介绍了向量组线性相关性的判断方法,由此可见,如果向量组的分量是具体给出的,则判断向量组线性相关性是较为简单的,总可用方程组的解,矩阵的秩和行列式的值的方法来判断.如果向量组的分量没有具体给出,则熟练理解和掌握向量组线性相关性的定义、定理等知识是解题的必要条件,要灵活运用向量组线性相关性的定义、定理等知识和技巧才有助于提高分析解决问题的能力. 〔1〕同济大学数学教研室.线性代数[M].北京:高等教育出版社,2007. 〔2〕张禾瑞,郝新.高等代数[M].北京:人民教育出版社,1986. O151.24 :A :1673-260X(2013)01-0007-02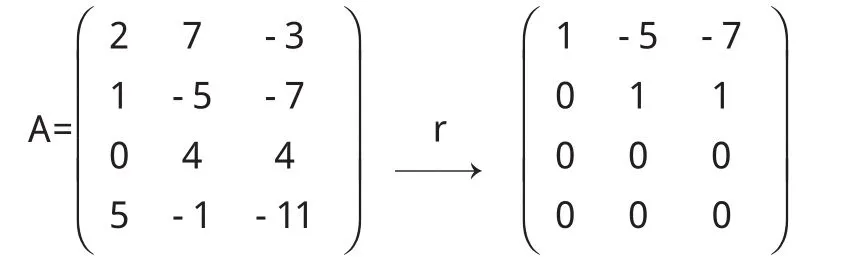

2 分量未给出的向量组线性相关的判断