刚-柔性机械臂动力学建模及其动力学特性研究
郭振锋,金国光,畅博彦,王 艳
(1.天津工业大学机械工程学院,天津 300387;2.天津工业大学天津市现代机电装备技术重点实验室,天津 300387)
刚-柔性机械臂动力学建模及其动力学特性研究
郭振锋1,2,金国光1,2,畅博彦1,2,王 艳1,2
(1.天津工业大学机械工程学院,天津 300387;2.天津工业大学天津市现代机电装备技术重点实验室,天津 300387)
根据假设模态法,对刚-柔性机械臂系统进行了位形表达及运动学分析.基于Kane方程,建立了刚-柔性机械臂系统的动力学模型.数值仿真结果表明,截取前二阶模态即可满足刚-柔性机械臂系统的精度要求;分析了柔性机械臂的结构参数、材料参数和驱动力矩对其动力学特性的影响.研究结果表明:通过采用矩形截面,采用较大弹性模量的材料,减小外部施加的驱动力矩,避免驱动力矩产生突变,可以有效地提高刚-柔性机械臂系统的动力学性能.
柔性机械臂;模态分析;Kane方程;动力学特性
柔性机械臂是一个高度非线性、强耦合、时变的动力学系统.与刚性机械臂相比较,柔性机械臂具有精度高、质量轻、操作空间大、成本低等优点,这使得柔性机械臂在精密仪器、航空航天等领域应用越来越广泛.但是,由于柔性机械臂在运动过程中会产生弯曲、剪切等弹性变形,引起机械臂末端弹性变形误差,从而影响机械臂的工作精度.Korayem等[1]用有限元法和拉格朗日方程建立了二自由度柔性机械臂的动力学模型;王斌锐等[2]基于假设模态法和Lagrangian原理建立了综合考虑关节和杆件柔性的刚柔耦合动力学方程;金国光等[3]用有限元法对柔性曲线梁离散化处理并应用Kane方程建立了动力学模型;Vakil等[4]结合假设模态方法和拉格朗日方程对双柔性机械臂进行动力学建模;裴希伍等[5]基于假设模态法、拉格朗日法和系统动量守恒对柔性连杆进行近似描述,忽略高阶弹性振动模态,推导了一种自由浮动空间柔性机械臂操作刚性有效载荷的动力学模型;崔玲丽等[6]应用有限差分法和有限元法建立了匀质单连杆柔性机械臂系统的模型;代小林等[7]运用凯恩方程推导了并联运动平台的多刚体动力学模型;孙占庚等[8]采用假设模态法和凯恩方程对建立了单自由度柔性臂的模型.本文基于假设模态法并结合Kane方法对刚-柔性机械臂系统进行动力学建模,并应用Matlab软件对其进行了仿真研究;根据仿真结果研究该系统的动力学特性,并分析影响弹性振动的因素.
1 刚-柔性机械臂动力学建模
在对刚-柔性机械臂进行动力学建模之前,作如下假设:
(1)只考虑柔性机械臂的横向振动,忽略其轴向变形和剪切变形;
(2)柔性机械臂横向变形为小变形;
(3)柔性机械臂的长度远大于其截面尺寸.
在水平面内作回转运动的刚-柔性机械臂系统如图1所示.

图1 刚-柔性机械臂的物理结构模型Fig.1 Rigid-flexible manipulators physical structure model
图1中,杆1为刚性杆,杆2为柔性杆;关节O1、O2均为转动副.在t瞬时,质点P的横向变形用u表示,则u是点P的坐标和时间t的函数,可记为u=u(x,t).设笛卡尔坐标系OXY为该机械臂系统的固定坐标系,坐标系O1X1Y1和O2X2Y2为该系统上分别固连在杆1和杆2上的动坐标系.τ1、τ2分别为关节O1和关节O2处加载电机的驱动力矩,m1r、m2r分别为关节O1和关节O2处电机的集中质量,l1、l2分别为刚-柔性机械臂系统上杆1和杆2的长度,h1、h2分别为杆1和杆2的截面高度,b1、b2分别为杆1和杆2的截面宽度,ρ1、ρ2分别为杆1和杆2的密度,m为柔性杆2末端所受的集中质量,θ1、θ2分别为杆1和杆2的关节转角.
点为柔性机械臂杆2轴线上的任一点,u(x,t)为轴O2X2上距P点t时刻的横向变形.根据机械振动原理,均匀材料等截面梁弯曲自由振动微分方程为[9]:
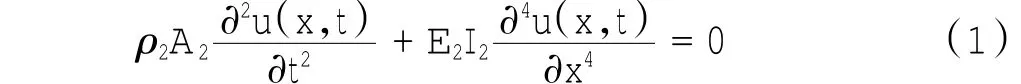
式中:ρ2为材料密度;A2为横截面积;E2为材料的弹性模量;I2为截面惯性矩.
式(1)的解可表达为:

式中:Φi(x)为柔性杆2的第阶振型函数;qi(t)为与振型函数相对应的模态坐标.
柔性机械臂的边界条件为:

式中:i=1,2,3,….
将柔性机械臂的边界条件(3)代入式(1),得到振型函数:
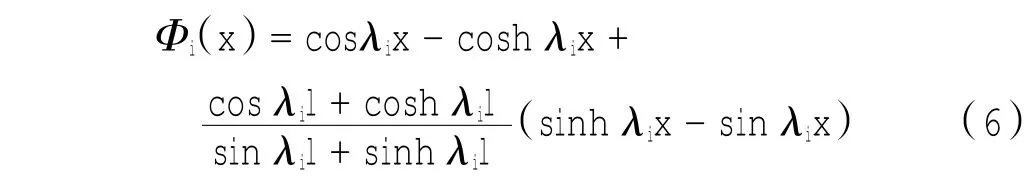
在实际应用中,一般取前n阶模态,同样可以得到较高的精度,所以将u(x,t)写成如下形式:

柔性机械臂在水平面内的运动可以看作是大范围刚体运动和小范围弹性变形运动的叠加,因此P点位置在体坐标系O2X2Y2中的坐标(XP,YP)可表达为:

柔性杆2上任意一点P在变形后,在体坐标系O2X2Y2中其位置矢量为:
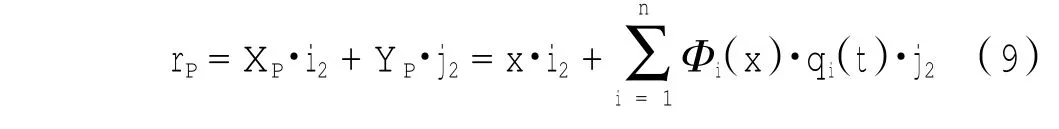
式中:i2,j2分别为柔性杆2在体坐标系O2X2Y2沿两个坐标轴的单位矢量.
若柔性机械臂上任意一点P小变形u(x,t)在体坐标系O2X2Y2中的速度为UP,则柔性机械臂上任意一点P在惯性坐标系OXY中的速度为:

式中:Ω2为柔性机械臂的角速度.
柔性机械臂内力的广义主动力为:

式中:Ki为柔性机械臂杆2的模态刚度矩阵.
其中

对于刚-柔性机械臂系统外部施加的驱动力和驱动力矩的广义主动力:

对于刚-柔性机械臂系统,应用Kane方法对其建立动力学方程,可得:

选取广义速率为θ˙1,θ˙2,q˙i(t).进行线性化处理,忽略耦合项和非线性项,得到如下线性化方程
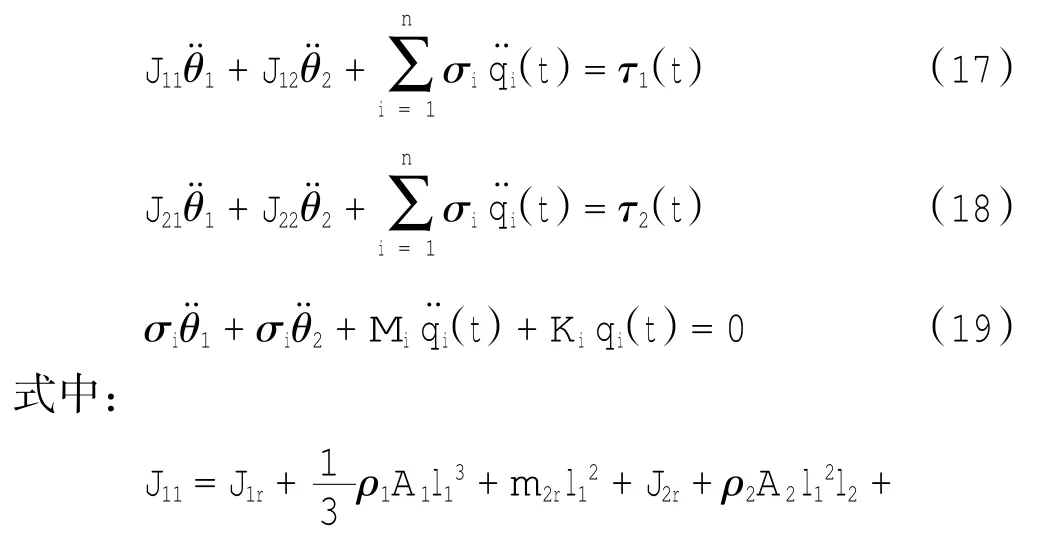

式中:J1r、J2r分别为电机转子对关节O1和O2中心的转动惯量.将式(17)~式(19)写成矩阵的形式,得到如下的方程式:

式(20)即为刚-柔性机械臂动力学方程.
2 刚-柔性机械臂系统的仿真研究
图1中,刚性杆1的长度l1=1.0 m,密度ρ1=7 800 kg/m3,截面宽度b1=0.04 m,截面高度h1=0.04 m,材料为普通碳钢.柔性杆2的密度ρ2=2 700 kg/m3,弹性模量E2=70 GPa,杆长l2=2.0 m,截面宽度b2= 0.04 m,截面高度h2=0.04 m,铝制材料.关节O2处电机的集中质量m2r=1.0 kg,柔性机械臂末端集中质量m=3.4 kg.关节O1处加载的力矩τ1=0.8 N·m,关节O2处加载的力矩τ2=(1-t)N·m.
初始条件:

仿真时间T=2 s.
从理论上讲,柔性机械臂的动力学模型是连续无限维的,其中包括刚性大范围运动以及无数个模态坐标.一般来讲,对仅考虑柔性机械臂振动的离散化动力学方程,模态阶数取得越多,其数值求解结果就越逼近实际情况.然而随着模态阶数的增加,求解的计算量就越大,这在实际应用中是不必要的.分别取系统前一阶模态、前二阶模态和前三阶模态作运动仿真,其仿真结果如图2所示.

图2 取不同阶模态柔性机械臂的动力学特性Fig.2 Dynamic performance with different modes of flexible manipulator
从图2中可看出,随着保留系统的模态阶数增加,柔性机械臂末端弹性变形差异变小,取前二阶与前三阶模态之间的差异非常小.为节约计算资源,同时保障误差很小的情况下,取系统的前二阶模态即可满足精度要求.
2.1 结构参数对柔性机械臂动力学特性的影响
柔性机械臂的结构参数包括柔性杆2的横截面形状.保持柔性机械臂的其他参数不变,加载力矩如图2所示,分别取不同的截面形状(等面积的方形截面、矩形截面(h2=4b2)和圆形截面)时,代人式(20)中,进行动力学仿真,如图3所示.

图3 取不同截面形状柔性机械臂的动力学特性Fig.3 Dynamic performance with different cross-section shapes of flexible manipulator
仿真结果表明:在柔性机械臂的横截面积相等的条件下,圆形截面的振动频率最低,末端弹性变形量最大;矩形截面的振动频率最高,末端弹性变形量最小,抑制弹性变形效果最好.
2.2 材料参数对柔性机械臂动力学特性的影响
柔性机械臂的材料参数主要包括柔性杆2的密度和弹性模量.保持柔性机械臂的其他参数不变,加载力矩如图2所示,分别取不同的密度ρ2=2 700 kg/m3、ρ2=4 500 kg/m3和ρ2=6 600 kg/m3,不同的弹性模量E2=70 GPa、E2=90 GPa和E2=110 GPa代人式(20)中,进行动力学仿真,如图4、图5所示.
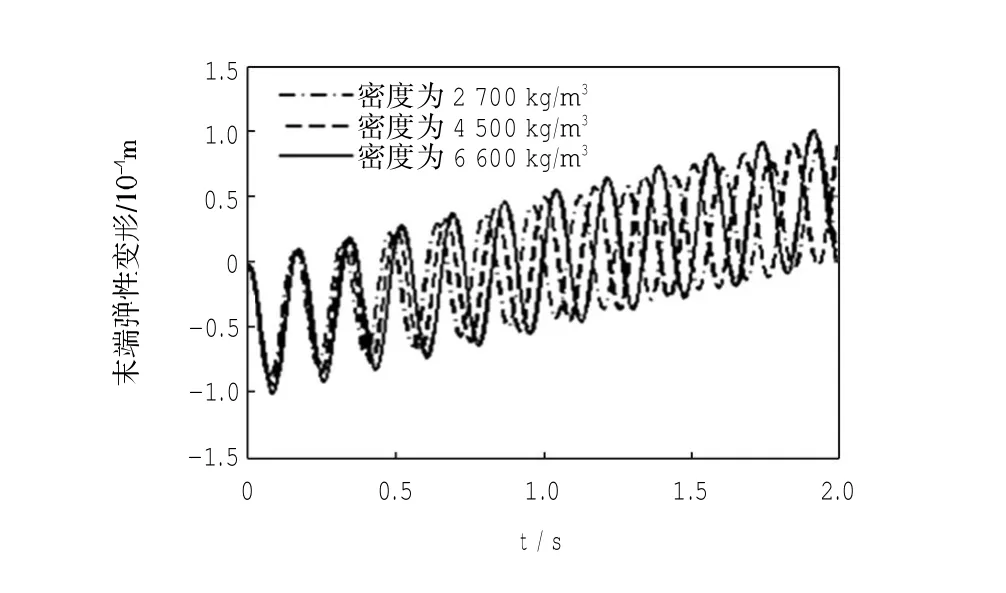
图4 取不同密度柔性机械臂的动力学特性Fig.4 Dynamic performance with different density of flexible manipulator

图5 取不同弹性模量柔性机械臂的动力学特性Fig.5 Dynamic performance with different elastic modulus of flexible manipulator
仿真结果表明:
(1)柔性机械臂的密度越大,振动频率越低,末端弹性变形程度对材料密度变化不敏感;
(2)柔性机械臂的弹性模量越大,振动频率越高,末端弹性变形程度越小.
2.3 驱动力矩对柔性机械臂动力学特性的影响
保持柔性机械臂的结构参数和物理参数不变,分别加载3种如图6所示不同的驱动力矩τ2=(1-t)Nm、τ2=0.8 Nm和τ2=t(2-t)Nm,代人式(20)中,进行动力学仿真,如图7所示.
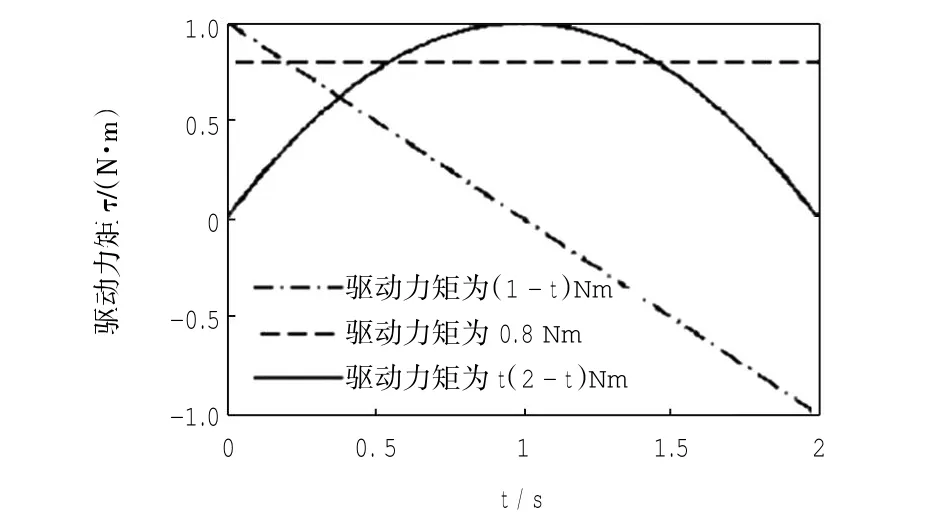
图6 加载在柔性机械臂上不同的驱动力矩Fig.6 Differentdrivingmomentsloadinginflexiblemanipulator

图7 取不同的驱动力矩柔性机械臂的动力学特性Fig.7 Dynamic performance with different driving moments of flexible manipulator
仿真结果表明:随着时间的变化,柔性机械臂的弹性变形程度与施加的驱动力矩变化趋势一致,即柔性机械臂末端弹性变形量随驱动力矩增大(减小)而增大(减小);比较图6和图7,初始时刻加载的力矩有突变时,柔性机械臂的振动较大.
综上所述,考虑到柔性机械臂的结构参数、材料参数以及外部施加的驱动力矩对其影响,由上述分析可知:若要改善柔性机械臂的动力学性能,即减小柔性机械臂末端的弹性变形及其振动频率,可以通过采用矩形截面,采用较大弹性模量的材料,适当减小外部施加的驱动力矩,尽量避免驱动力矩产生突变.
3 结束语
本文运用假设模态法和Kane方程建立了刚-柔性机械臂系统的动力学模型,并根据此模型对柔性机械臂系统进行动力学特性分析,研究了柔性机械臂的结构参数、材料参数和外加驱动力矩对系统动力学特性的影响,进而得出能有效减小和抑制柔性机械臂系统的弹性变形和振动的方法,为进一步研究柔性机械臂的振动稳定性、结构设计与结构参数优化提供了依据.
[1]KORAYEM M H,FIROUZY S,HEIDARI A.Dynamic load carrying capacity of mobile-base flexible-link manipulators:Feedback linearization control approach,December 15-18,2007[C].Sanya:IEEE,C2008.
[2] 王斌锐,方水光,金英莲.综合关节和杆件柔性的机械臂刚柔耦合建模与仿真[J].农业机械学报,2012,43(2):211-215.
[3] 金国光,刘又午,王树新.大范围运动的柔性曲线梁动力学建模及仿真[J].天津大学学报:自然科学版,2004,37(7):629-633.
[4]VAKIL M,FOTOUHI R,NIKIFORUK P N,et al.A study of the free vibration of Flexible-link Flexible-joint manipulators[J].Proceedings of the Institution of Mechanical Engineers,2011,225(6):1361-1371.
[5] 裴希伍,王从庆,吴鹏飞.自由浮动空间柔性机械臂轨迹跟踪与振动抑制[J].华中科技大学学报:自然科学版,2011,39(S2):28-31.
[6] 崔玲丽,张建宇,高立新,等.柔性机械臂系统动力学建模的研究[J].系统仿真学报,2007,19(6):1205-1208.
[7] 代小林,丛大成,韩俊伟,等.基于凯恩方程的并联运动平台多刚体动力学建模[J].液压气动与密封,2008(4):60-63.
[8] 孙占庚,金国光,常志,等.基于Kane法的柔性机械臂系统动力学建模及其模态截取研究[J].天津工业大学学报,2009,28(4):61-63.
[9]羊拯民.机械振动与噪声[M].北京:高等教育出版社,2011:92-94.
Research of dynamic modeling and performance for rigid-flexible manipulators
GUO Zhen-feng1,2,JIN Guo-guang1,2,CHANG Bo-yan1,2,WANG Yan1,2
(1.School of Mechanical Engineering,Tianjin Polytechnic University,Tianjin 300387,China;2.Tianjin Key Laboratory of Advanced Mechatronics Equipment Technology,Tianjin Polytechnic University,Tianjin 300387,China)
Judged by the assumption mode method,configuration expression and kinematic analysis were used to investigate the rigid-flexible manipulators system.Based on Kane's equation,the dynamic model of rigid-flexible manipulators system was established.Numerical simulation illustrates that interception before the second-order modes can meet the rigid-flexible manipulators system accuracy.The impact of different structures on the dynamic performance of flexible manipulator such as physical parameters,material parameters and driving moments were discussed.The results show that by using rectangular section,using larger elastic modulus of materials,reducing the external pressure driving moment,avoiding driving moment producing mutations can effectively improve the dynamic performance of rigid-flexible manipulators system.
flexible manipulator;mode analysis;Kane′s equation;dynamic performance
TH113.1
:A
:1671-024X(2013)01-0070-05
2012-09-18
国家自然科学基金项目(50675154);天津市应用基础及前沿技术研究计划项目(09JCYBJC04600)
郭振锋(1987—),男,硕士研究生.
金国光(1963—),男,教授,博士生导师.E-mail:jgg63@eyou.com

