用于机车牵引的新型级联H桥整流器电压平衡方法

顾春阳 郑泽东 李永东

（清华大学电机工程与应用电子技术系 北京 100084）

1 引言

在工业应用中，无论是以轧钢、高速铁路和船舶为代表的传统电气传动领域，还是以风力发电、光伏及微电网等为代表的分布式可再生能源领域，电力电子变换器都往高电压大容量的方向发展。功率器件是制约高压大容量变频器发展的一个重要因素。级联H 桥整流器（Cascaded H-Bridge Rectifier,CHBR）是解决现有电力电子功率器件耐压等级和电力电子变流器高压大功率之间矛盾的有效的技术方案[1,2]。级联H 桥整流器的控制目标是每个模块输出直流电压和输入交流功率因数。在不同的应用领域中，输出电压的目标可能是不同的，每个模块的负载条件也可能被改变。由于级联H 桥整流器每个模块的电流是相同的，因此直流电压的控制比较困难。直流电压的平衡方法成为这种拓扑结构的研究热点[3]。

文献[4]中，一种使用PI（比例积分）调节器的电压平衡控制方法被提出，将各级直流电压采集回来与给定值相比较，经PI 调节器输出后作为每个模块的占空比。但是，这种方法没有明确的PI 参数设置方法，模块之间的控制彼此制约，需要大量的时间和经验去调节多个PI 调节器的参数[5,6]。

除此以外，还有一些建立在非线性控制上的电压平衡控制算法，如无源性控制[7]等比较复杂，运算量大。文献[8]采用了滞环比较器的方法实现电压平衡控制，但这种方法没有固定的开关频率，使得相应的前端滤波器难以设计。

按照载波相位的不同，多电平的载波调制可以分为载波层叠、载波交叠和载波移相的方法。不同载波调制方式得到不同的PWM 输出电压波形，其谐波性能也有所不同。载波移相PWM 在H 桥级联变换器中广泛采用，但是电容电压平衡控制需要根据每个单元的电压高低由独立的PI 调节器生成不同的参考波，每个单元都需要完全独立的PWM 控制信号。当级联单元数量太多时，控制器的设计和PWM 信号的生成都比较复杂。载波同相层叠正弦脉宽调制（Phase Disposition Sinusoidal Pulse Width Modulation,PD-SPWM）相对于载波移相PWM 来说具有较好的谐波特性[9,10]，但PD-SPWM 本身并没有使得级联 H 桥整流器具备直流电压平衡的能力。

本文提出了一种基于改进的PD-SPWM的新的电压平衡控制方法，省去了传统均衡算法中的多个电压PI 调节器：①本文给出了级联H 桥整流器的控制原理；②提出并分析了基于改进PD-SPWM的电压平衡方法，这种方法即使在不平衡的负载和再生负载的条件下依然有效，因此可用于无变压器的机车牵引领域。仿真和实验结果表明了这种电压平衡方法的正确性和有效性。

2 级联H 桥整流器控制原理

在对级联H 桥整流器进行分析时，可以把变换器交流侧的级联电路看成一个整体，根据电压和功率相等的原则等效为一个PWM 整流电路，从而把H 桥级联型变换器的控制问题分成单相PWM 整流和电压平衡控制两个部分。

级联H 桥整流器的拓扑结构如图1 所示，共由N个H 桥模块组成。

各个模块交流输出电压和的瞬时值为uo，开关函数Si=di-d2N-i为第i个模块中两个半桥的占空比di和d2N-i之 差。

输入电流ig可由整流器的交流输出电压uo所控制。ug为电网电压，Rg和Lg分别为线路电阻和滤波电感。ui为第i个模块的交流输出电压，Udc,i为第i个模块的直流电压，Pi为第i个模块的负载功率。

图1 用于无变压器机车牵引系统的级联H 桥 整流器拓扑结构Fig.1 Topology of cascaded H-bridge rectifier for transformerless locomotive traction system

级联H 桥整流器的控制框图如图2 所示。H 桥级联整流器的控制目标为交流电流的波形、相位以及直流母线电压的大小，这与传统的单相PWM 整流器没有本质区别。而CHBR的拓扑结构决定了流到每一个H 桥的电流都相同，因此，对H 桥级联型多电平变换器的电流控制只能用一个电流环实现。

各个模块直流电压和的瞬时值与给定电压相比较，误差作为电压调节器的输入。电压调节器的输出为给定电网电流值的幅值，乘以电网电压相位得到电网电流给定值。电压调节器采用PI 调节器。为了使电网电压与电网电流同相位，电流调节器采用了PIR（比例-积分-谐振）调节器。为了抑制直流电压二倍工频脉动造成的电网电流的3 次谐波，各个模块直流电压和的反馈经过了一个带阻滤波器。

图2 级联H 桥整流器控制策略Fig.2 Control strategy of the CHBR

3 基于改进PD-SPWM的电压平衡控制

为了在得到较好谐波特性的同时实现直流电压平衡控制，本文提出一种改进的PD-SPWM 方法。采用这种改进的同相载波层叠SPWM 方法，整个系统只需要一路独立的PWM 信号即可，整流器控制和电压平衡可以解耦分别实现，易于扩展到更多电平，具有很强的通用性。

3.1 级联H 桥整流器的电压电流关系

在任一瞬间，每个模块有三种可能的工作模式：S=1 模式、S=0 模式和S=-1 模式。当Si=1 时，电网电流反向流过该模块，输入电流为-ig，交流电压为Udc,i；当Si=0 时，该模块被旁路，交流电压为零；当Si=-1 时，电网电流正向流过该模块，交流电压为-Udc,i。

对于级联的H 桥整流器的N个模块，有许多冗余状态的开关状态可用于电压平衡控制。对于第i个模块，如图3 所示，直流电压满足

式中，Ci为电容值；iLoad,i为负载电流；iC,i为电容电流。

图3 第i 个模块电压电流关系Fig.3 Voltage and currents of module i

对于变换器来说，负载电流和负载功率是不可预知的，因此iLoad,i可以被当做扰动来考虑。由式（1）可知，直流电压的变化率与开关函数Si和电网电流ig有关。电网电流周期性变化，且由负载决定，因此应通过控制开关函数Si来实现直流电压的平衡控制。

对于级联H 桥整流器

且

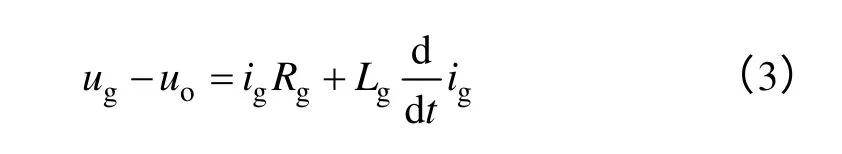
假设每个模块的直流电压均为dcU，由式（2）与式（3）可知

即

也就是说，当电网电压的控制目标确定时，任意时刻的各个模块开关函数之和Ssum也是确定的。对于PD-SPWM 模式，在一个开关周期内，仅有一个模块处于PWM 状态，其余模块均处于正向接入、反向接入或旁路状态。因此，根据每个模块直流电压大小确定Ssum在各个模块中的分派，即可实现基于直流电压的平衡控制。

电压平衡控制算法中电容电压采样可以是每个载波周期采样一次，也可以是数个载波周期采样一次。电容电压平衡控制算法输出各个单元的工作模式，PWM 模式中占空比由参考波与载波比较得到。

3.2 基于改进的PD-SPWM的电压平衡方法

根据上述分析，可得到具体的基于改进PD-SPWM的直流电压平衡控制方法的具体步骤如下：

（1）测量每个模块的直流电压以及电网电流，将直流电压偏离给定值的比率按由小到大的顺序排列，如图4a 所示，可设排序后的直流 电压偏离比率为。

图4 基于改进的PD-SPWM的电压平衡控制示意图Fig.4 Sketch of voltage balancing control based on improved PD-SPWM

（2）列举可能的无PWM 时的开关状态，并分配给所有模块，使得H+M+L=N，M≥1，且当ig≥0时L-H-1≤Ssum≤L-H+1（使L个模块正向接入，H个模块反向接入，M个模块旁路）；当ig＜0 时，H-L-1≤Ssum≤H-L+1（使H个模块正向接入，L个模块反向接入，M个模块旁路），其中L为电压较低的模块个数，H为电压较高的模块个数，M为电压始终的模块个数。

（3）将M个模块中电压最高或最低的模块改为PWM 模式，使得式（2）被满足，如图4b 和图4c 所示。

（4）将上述三个步骤中得到的所有可能的方案带入到评价指标公式中，取评价指标fgrade最高的方案作为下个开关周期的输出。

3.3 电压平衡方案的评价指标选择

由式（1）可知，模块直流电压的变化率

不同评价指标的控制方案的控制性能不同。

这里选定开关状态的所有模块直流电压变化率的绝对值之和作为评价指标，忽略负载电流的影响，则评价指标表示式为

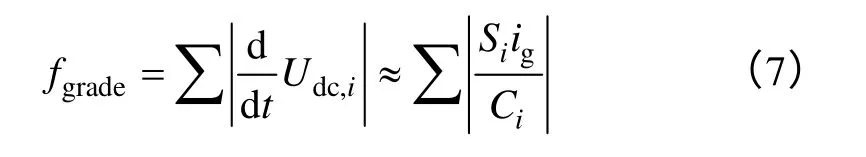
4 仿真与实验验证

为了验证所提出的电压平衡方法的有效性，在Matlab/Simulink 中搭建了系统的仿真模型，并进行了仿真实验。

仿真模型由4 个H 桥模块级联而成。电网电压的幅值为160V，频率为50Hz，PWM 等效开关频率为10kHz，总直流电压的给定值为200V。仿真结果如图5 所示。每个模块直流电压的平衡控制得以实现，负载电压是一个9 电平的PWM 波，交流电压和电网电流的质量得到改善。

为了进一步验证算法的有效性，设计并搭建了一个小功率实验平台，如图6 所示，并在此基础上了进行了9 电平的带均衡负载、非均衡负载和回馈负载的实验。

图5 仿真结果Fig.5 Simulation results

图6 实验平台Fig.6 Experimental platform

实验的具体参数见下表。

表 实验参数Tab. Experimental parameters

负载不均衡时的实验结果如图7 所示，这种情况下的控制策略的有效性得到验证。其中，模块1、模块2 和模块4的负载电阻为20Ω，模块3的负荷电阻为26.2Ω。

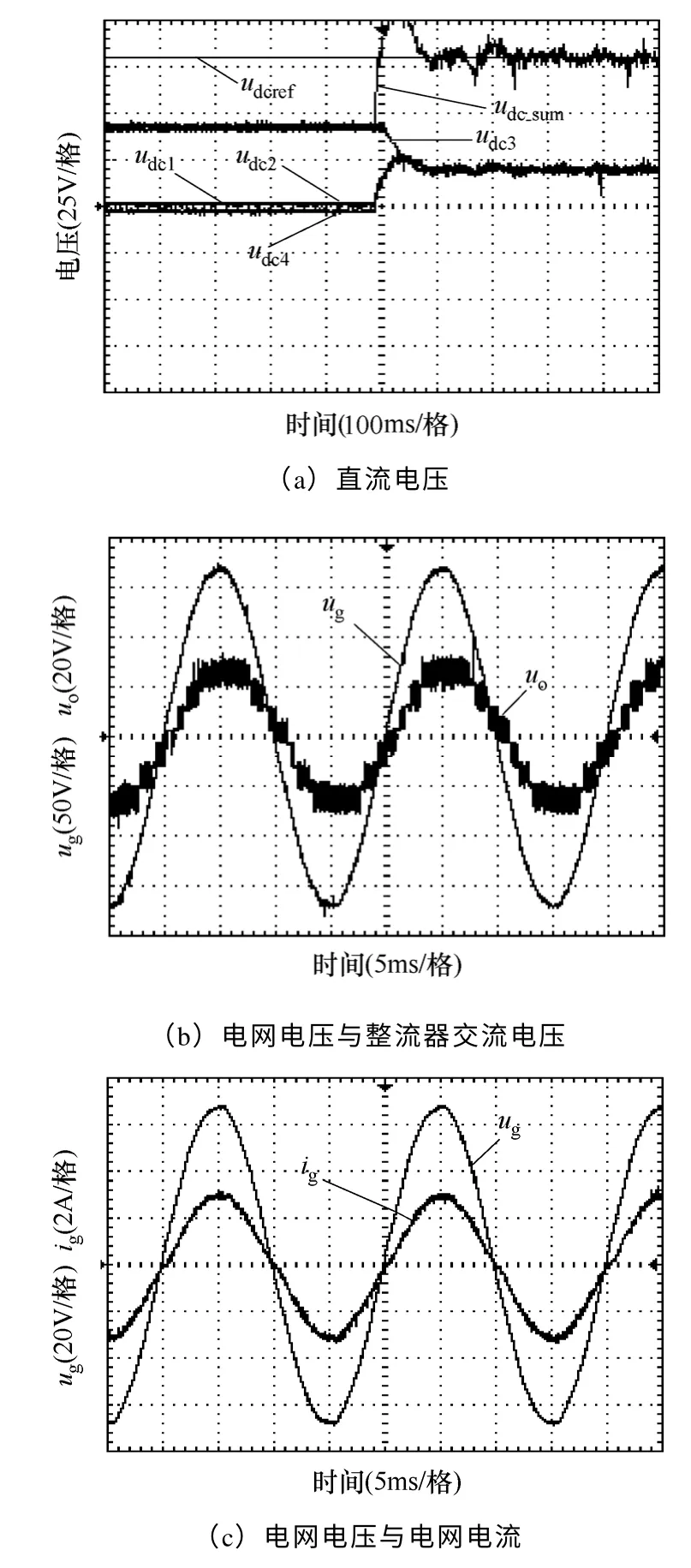
图7 负载不均衡时的实验结果Fig.7 Experimental results with unbalanced resistant loads

带回馈负载的实验结果如图8 所示。其中，模块1、模块2 和模块4的负载电阻为20 Ω，模块3的负载由一个37.8V的直流电压源和26.2Ω的电阻串联，回馈电流约为0.68A。

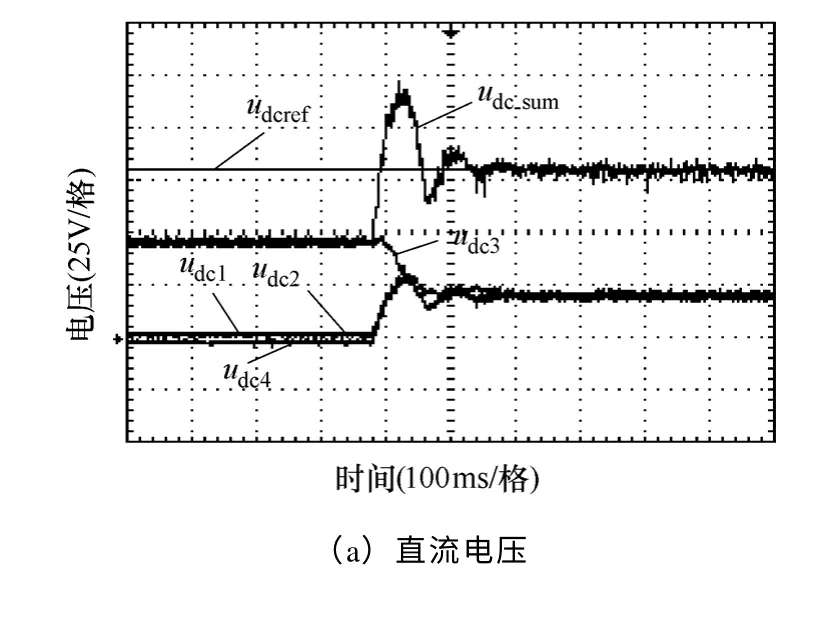
图8 带回馈负载时的实验结果Fig.8 Experimental results with a regeneration load

实验结果证实了这种电压平衡方法在应用于机车牵引时当某些电机处于回馈制动状态时的有效性。

5 结论

级联H 桥整流器可以用作机车牵引变流器，以省去传统的主变压器，可以降低机车牵引系统的体积、重量和成本。本文提出了一种新颖的使用改进的PD-SPWM 级联H 桥整流器电压平衡方法。与传统方法相比，该方法操作方便，稳定可靠，这种调制方法在保持了PD-SPWM 谐波特性的同时，实现了电压的平衡控制。在整流器带均衡负载和非均衡负载情况下，电压的平衡控制均稳定有效。特别是在某些模块的能量反向时，直流电压仍可平衡。仿真和实验结果表明了这种方法的正确性。

[1]Tao X,Li Y,Sun M.A phase-disposition PWM method for DC voltage balance in cascaded H-bridge rectifier[C].International Conference on Electrical Machines and Systems 2010,2010:243-248.

[2]Iman Eini H,Schanen J L,Farhangi S,et al.Design of cascaded H-bridge rectifier for medium voltage applications[C].Power Electronics Specialists Conference,2007:653-658.

[3]Watson A J,Wheeler P W,Clare J C,A complete harmonic elimination approach to DC link voltage balancing for a cascaded multilevel rectifier[J].IEEE Transactions on Industrial Electronics,2007,54(6):2946-2953.

[4]Dell Aquila A,Liserre M,Monopoli V G.Overview of PI-based solutions for the control of DC buses of a single-phase H-bridge multilevel active rectifier[J].IEEE Transactions on Industry Applications,2008,44(3):857-866.

[5]Rodriguez J R,Dixon J W,Espinoza J R,et al.PWM regenerative rectifiers:state of the art[J].IEEE Transactions on Industrial Electronics,2005,52(1):5-22.

[6]Vazquez S,Leon J I,Carrasco J M,et al.Analysis of the power balance in the cells of a multilevel cascaded H-bridge converter[J].IEEE Transactions on Industrial Electronics,2010,57(7):2287-2296.

[7]Dell Aquila A,Liserre M,Monopoli V G,et al.Passivity-based control of a single-phase H-bridge multilevel active rectifier[C].IEEE 2002 28th Annual Conference of the Industrial Electronics Society,2002,4:3117-3122.

[8]Iman Eini H,Schanen J L,Farhangi S,et al.A modular strategy for control and voltage balancing of cascaded H-bridge rectifiers[J].IEEE Transactions on Power Electronics,2008,23(5):2428-2442.

[9]Saeedifard M,Iravani R.Dynamic performance of a modular multilevel back-to-back HVDC system[J].IEEE Transactions on Power Delivery,2010,25(4):2903-2912.

[10]Anuradha K,Muni B P,Kumar A D R.Cascaded multilevel converter based DSTATCOM using p-q theory with DC link voltage balancing[C].International Conference on Power and Energy Systems 2011,2011:1-6.