基于正交实验的氧化锆陶瓷套圈内圆磨削研究
吴玉厚,王 强,王 贺,须 颖,张 珂
(沈阳建筑大学 交通与机械工程学院,辽宁 沈阳 110168)
0 引言
氧化锆陶瓷是一类抗金属腐蚀和化学腐蚀性能优异的先进的工程陶瓷材料。该材料具有高抗压强度,高硬度、耐磨损等性质,相比于轴承钢具有较低的密度,较低的热导率以及耐腐蚀、抗氧化和良好的耐热等性能,特别是氧化锆增韧材料,具有优异的韧性,可作为热机、陶瓷套圈等耐磨机械部件,并且能够在某些场合替代传统的金属材料[1]。
氧化锆陶瓷材料的高硬度和高耐磨性,给其自身的加工带来了一定的困难,磨削是加工氧化锆的主要方法之一,且加工过程需要较高的砂轮线速度。国内外对氧化锆等陶瓷材料的磨削机理已进行了较多的研究,但是关于磨削参数对表面粗糙度的研究,还有待进一步的深入。本论文通过设计磨削参数的正交实验,系统地研究了磨削工艺参数包括砂轮粒度,砂轮线速度vs、轴向振荡速fa、径向进给速度fr等对磨削表面粗糙度Ra的影响,为合理选择磨削工艺参数提供了借鉴和帮助。
1 实验条件和方法
实验采用无锡机床厂生产的MK2710型数控内外圆复合磨床,对氧化锆增韧陶瓷轴承外圈内圆进行磨削。磨削工具采用树脂结合剂金刚石砂轮,砂轮浓度为100%,砂轮外径50mm,厚度5mm,宽度7.56mm。实验套圈样件为氧化锆增韧陶瓷工件,尺寸为(68×58×15)mm。磨削液采用油水比例为1∶20水基磨削液,并于每次磨削实验完成后,测量氧化锆陶瓷材料的磨削面粗糙度值Ra。采用精度达0.001μm Surtronic25型接触式粗糙度仪,对磨削后的表面状态进行测量。
本文采用正交设计的实验方法,正交因素水平如表1所示。以金刚石砂轮的粒度(#),金刚石砂轮的线速度vs,轴向振荡速度fa,径向进给速度fr四个加工参数作为实验的主要因素,其中每个因素选取三个实验水平;以氧化锆陶瓷材料的被磨表面粗糙度值Ra为实验指标,利用四因素三水平L9(34)正交表进行实验。
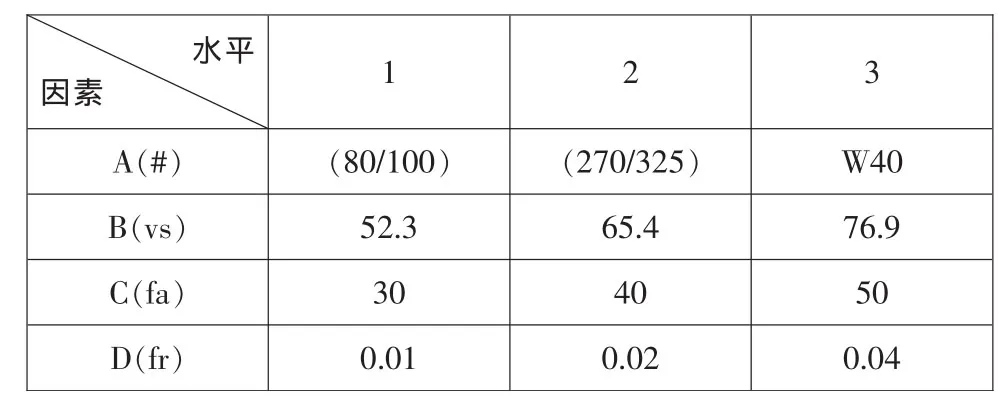
表1 正交实验因素水平表Tab.1 Table of orthogonal experimental factors level
2 正交实验结果及其分析
正交实验方案和实验结果如表2所示。
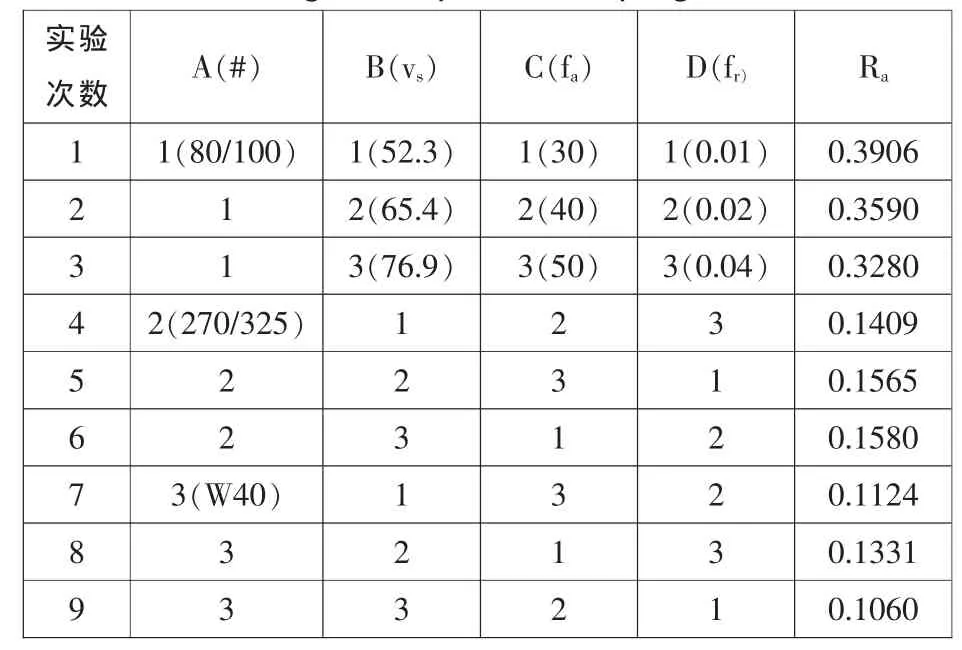
表2 正交实验方案及结果Tab.2 The orthogonal experimental program and results
2.1 实验数据直观分析
表3列出的是粗糙度值Ra的极差分析内容。在极差分析表中, Ki(i=1,2,3)表示每一列中该因素对应的不同水平号实验结果之和。R是极差,其意义为:
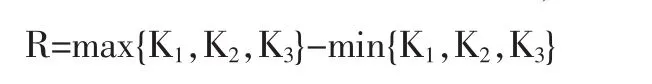
由表中结果可知,每一列极差值是不同的,意味着不同的因素水平变化对实验数据的影响不同。某一因素的极差改变越大,表示该因素水平的变化对实验指标的数值波动影响越大。于是,可得出极差值最大的那列,就是对实验结果影响最显著的因素。通过比对不同极差值,可选出各个因素的优化组合,称为优化方案。磨削氧化锆套圈实验中,粗糙度值Ra越小越好,故选择上要侧重于指标小的水平,即Ki中各列最小数值对应的水平。
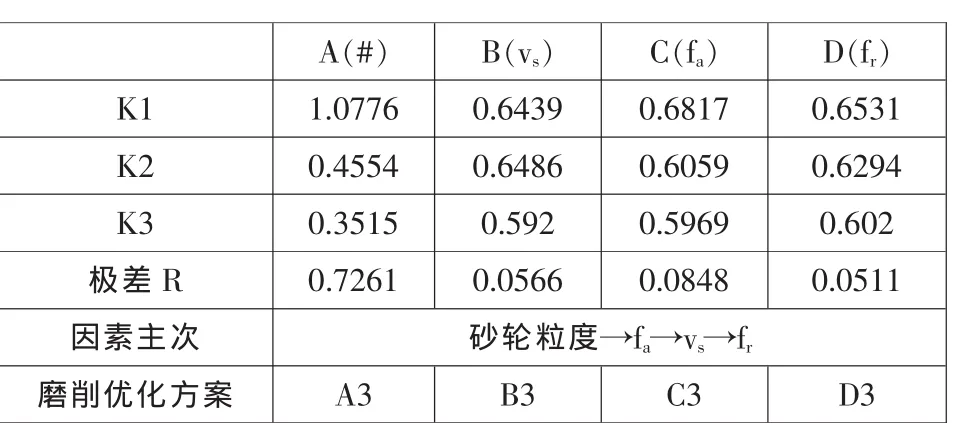
表3 粗糙度值Ra极差分析表Tab.3 Table of roughness Ra range analysis
2.2 对实验结果进行回归分析
在磨削实验过程中,砂轮粒度R值较大,可认为对磨削面的表面状态影响作用显著。砂轮线速度、轴向振荡速和径向进给速度的R值较小,可认为对磨削面的表面状态影响作用不显著。为了更加深刻的探究这些参数跟Ra的关系,具体分析各个因素对Ra值的影响大小,我们建立如式(1)的指数形式的预测数学模型,kφ为砂轮颗粒大小。

一般选择金刚石砂轮磨削陶瓷材料,砂轮中对陶瓷表面粗糙度影响最大的因素是金刚石磨粒的粒度。粒度号越大,其磨粒就越小,也就是说磨粒平均尺寸越小,其磨削出来的表面粗糙度值就越低。我们可以用磨削颗粒的算术平均值来表征粒度号的变化。经查,80/100#,270/325#,W40三种砂轮的金刚石磨粒平均大小为174μm, 58μm, 35μm。 设 lgCRa=b0, p=b1, l=b2, m=b3,q=b4。经过对式(1)的线性转化和正交回归计算得出Ra的回归方程:
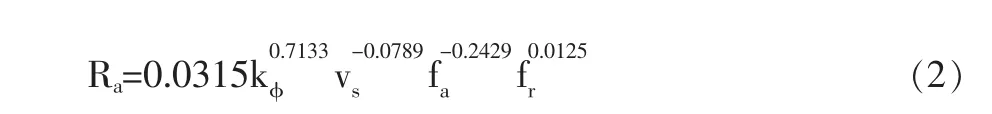
将表2中的实验因素带入回归方程式(2)中可得出如图1所示的Ra回归值与实验值的偏差图。图中横坐标代表的是实验序号,纵坐标是回归值与实验值之间的偏差,从图中可看出最大偏差尚未超过0.023μm,拟合效果比较好。
利用F统计量对回归方程式(2)进行检验:
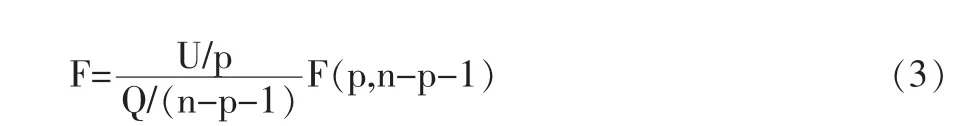
式中: n—实验组数(n=9);p—变量个数(p=4)。 取检验水平0.1,查表知F0.1(4,4)=4.11。由表4可以看出,经计算对于粗糙度所得的回归公式,F=47.18>4.11,可知所得的粗糙度回归公式显著,其很好地拟合了实验数据。
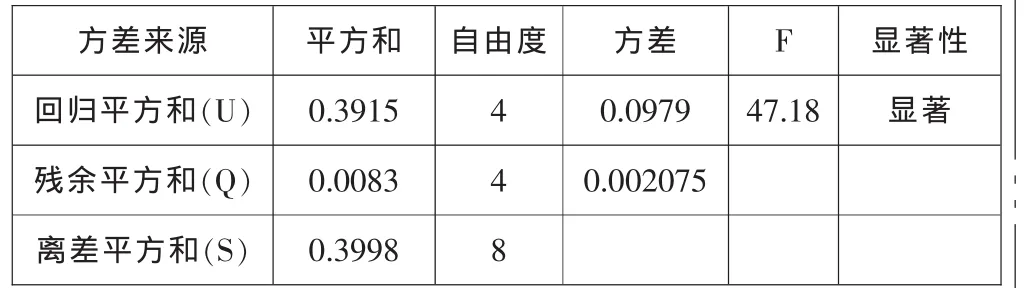
表4 回归方程方差分析表Tab.4 Regression analysis of variance table
2.3 粗糙度预测模型回归系数显著性检验
在实际应用中,当得知一个多元回归方程是显著的情况下,还要考察每个自变量对因变量的影响究竟有多大。我们需要考察自变量因素中哪些是影响因变量的主要因素,以利于我们更好地对粗糙度进行预测和控制,因此需要对每个自变量进行回归系数显著性检验。假设统计量b0=0,对其余统计量进行检验:
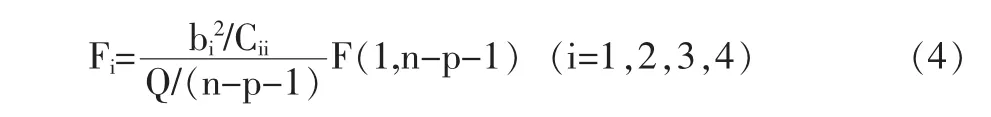
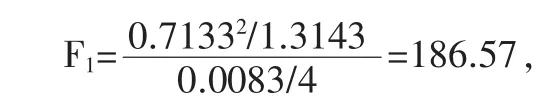
3 结论
基于正交实验,明确了不同磨削参数对加工氧化锆陶瓷套圈内表面粗糙度的影响。对实验结果进行了回归分析,得出氧化锆陶瓷套圈内表面粗糙度Ra的预测模型:

并对该预测方程和回归系数分别进行了显著性检验,得出结论:
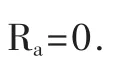
(2)经回归系数显著性检验,金刚石砂轮的粒度号变化对加工表面粗糙度的影响显著,而实验中砂轮线速度、轴向振荡速和砂轮径向进给速度的变化对加工表面粗糙度的影响不显著。
[1]张玉军,张伟儒.结构陶瓷材料及其应用[M].北京:化学工业出版社,2005.
[2]吴玉厚,李颂华.数控机床高速主轴系统[M].北京:科学出版社,2012.
[3]李伯明,赵波.现代磨削技术[M].北京:机械工业出版社,2003.
[4]吴玉厚,吕艳.HIP-SN陶瓷轴承套圈磨削特性的实验 [J].沈阳建筑大学学报,2007,1.
[5]吴玉厚,王凯,李颂华.内圆磨削HIPSN工程陶瓷磨削力的实验研究 [J].沈阳建筑大学学报,2008,5.
[6]吴玉厚,王贺,李颂华,张珂,佟俊.高速电主轴用陶瓷轴承套圈内表面磨削实验研究[J].2007,10.
[7]费业泰.误差理论与数据处理[M].北京:机械工业出版社,2005.
[8]Sanjay Agarwal,P.Venkateswara Rao.A probabilistic approach to predict surface roughness in ceramic grinding.[J]International Journal of Machine Tools& Manufacture 45,2005.
[9]Han Huang, Ling Yin, Libo Zhou.High speed grinding of silicon nitride with resin bond diamond wheels[J].Journal of Materials Processing Technology 141,2003.
[10]Han Huang.Machining characteristics and surface integrity of yttria stabilized tetragonal zirconia in high speed deep grinding[J].Materials Science and Engineering A345,2003.
[11]W.Li, Y.Wang, Shouhong Fan, Jinfu Xu.Wear of diamond grinding wheels and material removal rate of silicon nitrides under different machining conditions[J].Materials Letters 61,2007.
[12]张继鹏,吴玉厚,张 珂,张丽秀,李颂华.工程陶瓷主轴沟道表面磨削加工的实验研究[J].机电产品开发与创新,2010,1.

