数字系统投影时序逻辑描述及验证
张鹏飞,叶永升
(1.淮北师范大学 计算机科学与技术学院,安徽 淮北 235000;2.淮北师范大学 数学科学学院,安徽 淮北 235000)
数字系统投影时序逻辑描述及验证
张鹏飞1,叶永升2
(1.淮北师范大学 计算机科学与技术学院,安徽 淮北 235000;2.淮北师范大学 数学科学学院,安徽 淮北 235000)
投影时序逻辑是一种具有离散时间模型的时序逻辑,其部分子集又是一种程序设计语言,可处理顺序和并发计算.文章讨论应用投影时序逻辑对数字系统进行形式描述和验证的方法,该方法可在数字系统的不同层级设计过程中,使用投影时序逻辑对其系统行为和性质进行形式化的描述及验证,从而提高系统设计的可信性.
投影时序逻辑;形式化描述;系统验证
电器设备的数字化以不可阻挡的趋势成为当今电器设计的主题,从小到大的电器设备被加上或将被加上数字之芯.在数字系统设计中,在经过一系列步骤后,才能把设计思想转化为具体的产品.随着系统复杂性的提高,如何对系统进行描述以避免产生歧义,如何对系统进行验证以保证系统的活性和安全性也是数字系统设计中的重要问题.现阶段数字系统设计的各阶段所用的描述语言不仅不同,而且缺乏精确的数学语义,不能保证各级描述的一致性.在验证方面,传统的验证方法由于不能提供系统的完整覆盖,所以不能在未发现错误时确认系统无错误.形式化方法起源于20世纪60年代的软件危机,是一种基于数学的描述和验证方法,用以提高设计的正确性和可靠性.在保证软件和硬件设计正确性方面,形式化方法的使用和研究取得了很多成果.
投影时序逻辑(Projection Temporal Logic)是一种离散区间或时段的时态逻辑,具有在统一数学框架下对实时、并发系统进行形式描述和验证的能力.投影时序逻辑的优点在于它的表达能力强,既能刻画系统的性质又能表示系统的实现,系统的验证可在统一的数学模型框架下进行.除定理证明和模型检测之外,PTL具有可执行子集MSVL语言,可通过编写并执行规范程序的方式来达到验证的目的.所以应用投影时序逻辑对数字系统进行形式化描述,可为数字系统设计及其验证提供一系列的支持,提高数字系统设计正确性.
1 投影时序逻辑
1.1 语法
设∏是命题的可数集合,V是有类型定义的静态变量和动态变量的可数集合(在区间内其值保持不变的称静态变量,否则为动态变量).项(terms)和公式(formulas)由下列语法给出.

其中x是一个动态变量,u是一个静态变量.在f(e1,…,em)和P(e1,…,en)中,f是一个函数而P是一个谓词,假定项的类型和f及P中的类型相兼容.公式(项)被称为是状态公式(项)如果它不含任何时序操作符;否则是一个时序公式(项).
1.2 语义

2 数字系统的投影时序逻辑描述
随着数字系统的日益复杂,在系统开发的各个阶段写出清晰、完整和一致的系统规范是件十分重要的事情.数字系统设计各阶段的规范工具既不统一又缺少精确的数学语义,而模拟形式的验证也不能保证设计的正确性.投影时序逻辑既可作为有精确语义的形式化的规范工具,又可以用来描述系统的某些重要性质(如安全性和活性),这样为在统一数学框架内对系统性质进行形式验证提供了方便.
2.1 硬件的行为语义
1)时态赋值
延时是电路中的常见现象.设A是一个输入信号,B是一个与A对应的输出信号.在每个长度为1个单位的子区间,输出信号B在区间结束时的值等于输入信号A在区间开始时的值,这称为单位延时.在投影时序逻辑中对延时进行定义后就可以用来验证系统的一些时间性约束性质.

表示如果某个区间(时间段)内表达式A的初始值等于表达式B的终值,此处a为一个静态变量.单位时态赋值,表示电路从一个状态变化到另一个状态的区间长度是1,变化后x的值为e.

2)时态相等
如果当两个表达式在一个区间内永远相等时,称这两个表达式是在该区间时态相等的.

3)信号的稳定性
如果一个信号的值在所考虑的时间段内固定不变,则称该信号是稳定的.信号的稳定性可用stb操作符表示.


2.2 组合逻辑电路描述
最基本的组合逻辑电路如与门、或门、非门、三态门,如果不考虑时延,对这种电路用投影时序逻辑公式可描述为:

三输入与门可用两个两输入与门适当连接而成,对其公式的描述可用两个与门的投影时序逻辑公式相与而得到.

可以证明这两种公式是等价的.这说明使用投影时序逻辑对电路进行建模具有抽象性,设备无关性,适合电路的高层设计.

图1 多路选择器的框图及逻辑功能
使用投影时序逻辑可对组合逻辑电路进行描述.图1是一个2-to-1多路选择器,从逻辑功能上,该电路可用下式描述(I0表示信号Input0,I1表示信号Input1):

如果考虑电路的时间延迟(设延迟时间为n个时间单位),则其行为可用下式描述:
pMUX(E,S,I0,I1,Output,n)=def(if(E=0)then Z)else(if S=0 then I0)else I1))delnOutput.
2.3 基本时序元件
基本时序元件是锁存器、触发器,其中D触发器(锁存器)最为常用.下面通过实例说明投影时序逻辑对基本时序元件建模的方法.
如图2a是一个正向边沿触发的D触发器功能表.当LD=0时,不论输入端是什么信号,D触发器状态保持不变,而当LD=1且时钟信号从0到1变化,则D触发器的状态变为D的输入信号.当LD=1但时钟信号不是从0到1变化,则D触发器的状态也不变.
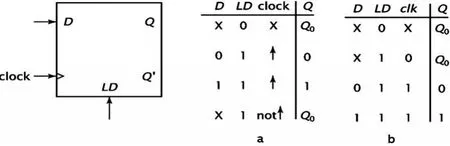
图2 D触发器(锁存器)

图3 D触发器组成的4位计数器

2.4 寄存器传送语言(RTL)
RTL用于描述微操作执行数据传送的条件和过程.RTL独立于实现系统的元件,同一RTL代码可以用不同的电路实现.但RTL又是最接近实际电路设计的一种抽象描述,使用RTL对系统行为进行描述后,就可以用硬件来匹配这些规范,从而得到具体的数字电路.RTL是对更高层系统描述—状态图进行分析处理而得到的,所以又可以认为是状态图这一系统规范的实现.在所有RTL代码中,时钟信号是隐含的.RTL的符号形式:
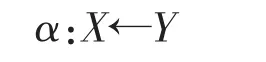
其中X←Y表示数据从寄存器Y流入X,α表示发生这一传送的条件.
把RTL代码转化为投影时序逻辑公式是一件有意义的事,它可以用形式化方法检查所描述的系统是否能完成相应的功能,条件是否互斥,对寄存器的操作是否相矛盾等(例如不能对其同时进行清零和置数的操作).下面以一个模6计数器为例,说明如何使用投影时序逻辑对RTL代码进行描述.
模6计数器按000→001→010→011→100→101→000的规律计数.当输入信号U=0时,寄存器中值不变,当U=1时,在时钟脉冲上升沿到来后,寄存器中值加1.当计数器从5变到0时产生进位(C=1),图4是模6计数器的状态图表示.该计数器有8个状态(S0,S1,S2,S3,S4,S5,S6,S7),其中S6,S7用于解决电源开启时处于无效状态的情形

图4 模6计数器的状态图

图5 模6计数器的RTL代码

2.5 状态图

3 对数字系统的形式验证
在数字系统设计过程中,往往采用自顶向下的设计方法,首先给出系统的文字描述,然后使用诸如状态图之类的工具对系统建模,以描述系统的行为.再根据这个系统模型细化,使用寄存器传送语言或硬件描述语言对系统进行高层(或低层)设计,最后使用常用的集成逻辑部件来搭建实际电路.在每一级设计中的错误都会导致失败.投影时序逻辑在数字系统设计中除可以对系统的各级设计用统一的语言进行建模外,还可描述系统应满足的活性、安全性及时间约束等性质,这为使用模型检测技术或定理证明技术对系统级设计进行活性及安全性验证提供了方便.
psc是模6计数器的状态图描述公式,pRTL是模6计数器RTL描述公式,如果这个描述正确反映系统的顶层设计(状态图),则一定有|=pRTL→psc.pAND3(x,y,z,A)是三输入与门的行为描述公式,p′AND3(x,y,z,A)是用2个与门连接成的电路的公式,如果这个电路能正确实现三输入与门的功能,则在逻辑上可以推导出:

设pM是某数字系统模型的投影时序逻辑描述公式,pI是由该模型经细化后得到的更接近电路实现的模型描述公式,我们称前者是系统的规范,后者是系统的实现.如|=pI→pM成立,则称系统的实现pI满足系统的规范pM.

在投影时序逻辑中,通过验证系统级规范与RTL级实现间的满足关系、RTL规范与寄存器电路级间实现的满足关系可以形式地证明实际的电路和系统模型间的一致.
数字系统设计验证中的另一个问题是系统的活性、安全性及时间性约束问题.我们把系统应该具有的某些特征或约束称为系统的性质.投影时序逻辑可以很好地对这些性质进行描述.例如模6计数器在启动后,应满足在任何时候都不应有V>5的情况.这一系统的安全性问题用投影时序逻辑可表示为(V<6).所设计的系统(psc)是否具有这一性质,转化为验证|=psc→(V<6)是否成立的问题.如果|=pRTL→psc且|=psc→(V<6),则一定有|=pRTL→(V<6).所以有以下定理.

投影时序逻辑具有严格的语法和语义,其命题投影时序逻辑(PPTL)的判定性、表达性和复杂性问题已经得到解决,建立有PTL和PPTL的模型理论和公理系统.MSVL是以投影时序逻辑的可执行子集Tem⁃pura语言为基础,建模、仿真、验证为一体的形式化工具,和常见的程序设计语言不同,MSVL程序的执行实质是一个逻辑推理的过程.使用投影时序逻辑的模型检查技术或公理证明系统可以验证上面所讨论的公式满足关系.在开发的不同阶段用于描述数字系统的状态图、RTL、电路等经投影时序逻辑公式描述后,可以转化成MSVL程序以进行模拟验证.
4 结论
本文讨论了使用投影时序逻辑及MSVL语言对数字系统进行形式描述和验证的方法.把投影时序逻辑引入数字系统设计过程,通过对系统级和实现级的数字系统进行形式描述,可以使系统的设计更加清楚明确,如果系统的一些性质也用PTL公式来表示,就可在同一逻辑框架下对系统应满足的性质进行证明,同时可把系统形式描述转换为MSVL程序进行模拟.
[1]JURGEN R,ROLAND J,WEISS T K,et al.Modeling and formal verification of production automation systems[C]// INT2004,LNCS3174,Springer Verlag,2004:541-566.
[2]王永祥,吴尽昭,蒋建民.进程代数——对称与动作细化[M].北京:科学出版社,2007.
[3]林惠民,张文辉.模型检测:理论、方法与应用[J].电子学报,2002,30(12A):1907-1912.
[4]DUAN Z,KOUTNY M,HOLT C.Projection in temporal logic programming[C]//Proc 5th International Conference on Logic Programming and Automated Reasoning,Lecture Notes in Computer Science 822,Springer,1994:333-344.
[5]王小兵.面向对象MSVL语言及其在组合Web服务验证中的应用[D].西安:西安电子科技大学计算机学院,2009.
[6]CARPINELLI J D.计算机系统组成与体系结构[M].李仁发,彭蔓蔓,译.北京:人民邮电出版社,2003.
[7]DUAN Zhenhua,TIAN Cong.A unified model checking approach with projection temporal logic[C]//ICFEM2008,LNCS5256,Springer-verlag,2008:167-186.
[8]TIAN Cong,DUAN Zhenhua.Model checking propositional projection temporal logic based on SPIN[C]//ICFEM 2007,LNCS4789,Springer-verlag,2007:246-265.
[9]舒新峰,段振华.有穷时间投影时序逻辑的完备公理系统[J].软件学报,2011,22(3):366-380.
PTL Specification and Verification of Digital System
ZHANG Peng-fei1,YE Yong-sheng2
(1.School of Computer Science and Technology,Huaibei Normal University,235000,Huaibei,Anhui,China;
2.School of Mathematical Sciences,Huaibei Normal University,235000,Huaibei,Anhui,China)
PTL(Projection Temporal Logic)is a kind of temporal logic which can handle both sequential and parallel computa⁃tion.A formal approach of specification and verification of digital system using PTL is proposed in this paper.With this ap⁃proach,PTL and its executable subset(MSVL)are used for formal specification and verification in different level design of a digital system.
projection temporal logic;formal specification and verification;digital system
TP 301
A
2095-0691(2013)04-0061-06
2013-09-18
淮北市科技局基金项目(20120309)
张鹏飞(1968- ),男,安徽利辛人,硕士,研究方向:嵌入式系统形式化描述与验证.

