基于OSP与NMF的光谱混合像元分解方法
徐 君,展爱云,刘志伟
(华东交通大学信息工程学院,江西南昌330013)
高光谱遥感技术可以同时提供空间域信息和光谱域信息,得到地物近似平滑的光谱曲线,因此近年来广泛地应用在土地资源调查、环境监测、军事侦察等领域[1-3]。但大多数高光谱成像仪的空间分辨率并不高,这就导致在同一个像元中可能包含多种地物,所提取的光谱特征是多种地物光谱特征的混合,这种像元被称为光谱混合像元。混合像元的存在使得传统的基于像元级光谱统计特性的分类方法无法直接使用,这是因为直接将这类像元归属到哪一种典型地物都是不准确的,因此混合像元问题是遥感技术向定量化发展的重要障碍。混合像元中每种地物的比例成为地物分布的丰度,反演混合像元丰度的过程称为混合像元的解混。
一般光谱混合像元分为线性混合模型和非线性混合模型两类[4]。非线性光谱混合模型比较复杂、物理意义并不明确。线性光谱混合模型建立与解释相对容易,物理意义明确,精度能够满足大部分应用的要求。因此在一般情况下,可以用线性模型来描述混合像元的形成机理,大部分混合像元分解算法都是基于线性模型的。
非负矩阵分解[5-8](nonnegative matrix factorization,NMF)是20世纪末出现的一种盲源分解算法。由于NMF与线性光谱混合模型的公式之间有着很高的相似性,这就为NMF在混合像元分解中的应用提供了可能。将NMF应用于高光谱混合像元的分解不需要假定纯像元的存在,并且在提取端元的同时可以获取每种端元对应的丰度图。然而NMF的目标函数具有明显的非凸性,因而存在大量局部极小。对于NMF问题V≈WH,(V,W,H均为非负矩阵),可以找到大量的非负可逆矩阵D及其逆矩阵D-1,有WH=(WD)(D-1H)成立,这样可以得到很多对解WD和D-1H,这是NMF存在的最大的问题。
本文首先通过正交子空间投影(orthogonal subspace projection,OSP)技术估计端元的个数[9],然后通过改进的外包单形体最小体积约束非负矩阵分解算法(minimum volume constrained nonnegative matrix factor⁃ization,MVC-NMF)对高光谱混合像元进行分解[10],同时得到目标景物的端元光谱及丰度分布图。
1 基于OSP的端元估计算法
线性光谱混合模型的数学公式:

式中:X是高光谱图像中某个光谱混合像元的光谱矢量;A为m×n的端元矩阵;m为波段数目;n为端元数目;S为丰度矩阵;ε为噪声或模型的误差。
OSP算法的思想就是将式(1)转换为式(2)的形式:

式(2)中的端元信号可以表示为目标信号D和背景信号U的组合,fD和fU分别为对应的丰度。高光谱图像可视为由一组端元所张成的子空间中的高维数据点的集合,而OSP算法能实现目标和背景分离的关键就在于如何利用端矩阵A构造一个投影矩阵,从而能将光谱向量通过投影到空间的正交子空间中去。
本文所提算法需随迭代次数的增加逐步提取端元,并将其逐个加入到端元矩阵A中,相应的也随之增大。端元提取算法采用单形体生长算法(simplex growing algorithm,SGA),该算法能稳定的逐个提取端元,保证提取结果的一致性。采用高光谱图像中所有像元光谱矢量的平均值μ作为待投影的矢量来进行迭代,具体步骤如下:
1)对实验所用的高光谱数据进行去噪及几何校正等预处理;
3)设定迭代的终止条件阈值σ;
4)开始迭代,在每次迭代过程中都为端元矩阵Ai增加一个端元光谱ai,得到
2 改进的MVC-NMF混合像元分解算法
对于线性光谱混合模型而言,丰度矩阵S存在两个限制条件:非负性约束(abundance nonnegative con⁃straint,ANC)与和为一约束(abundance sum-to-one constraint,ASC)。如果不考虑其他条件,仅在这两个约束条件下NMF算法结果不具有唯一性。因此,在将NMF应用于光谱数据的线性解混时一般需要引入其他的约束条件。
根据凸面几何学的理论,高光谱数据位于由端元光谱作为顶点的单形体内,像元在单形体中的位置决定了混合像元各端元的丰度,而最优的单形体应该外包特征空间中的所有点且具有最小的体积,因此在NMF光谱解混算法过程中可以加入最小单形体体积约束来优化算法,实现混合像元的精确分解。
文献10中的算法正是通过求最大单形体的体积作为约束求解NMF算法而得到各个端元的,其体积公式如下:


式中:an是第n个端元的列向量;V(A)是由这n个端元作为顶点构成的单形体的体积。由于用到了求行列式的运算,所以要求A必须为方阵,这样向量an的维数必须是n-1,这就需要先对原始数据进行降维处理,因此计算可能导致偏差,这是此算法的不足之处。
由于m维单形体包含于m维平行多面体中,因此它们的体积对应关系为为m维单形体体积,为m维平行多面体体积。
假设a1,a2,...,an是光谱图像图像中的n个像元的光谱矢量,如令则在特征空间中,以这n个点为顶点的平行多面体体积为,因此以这n个点为顶点的n-1维单形体体积J(Vn)可通过下式计算:

式(5)表示的单形体体积计算公式对于任何维数的高维空间都是成立的。据此可以构建改进后的最小体积约束MVC-NMF目标函数:
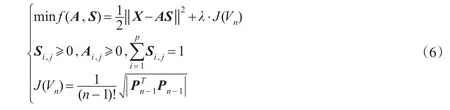
式(6)中λ=00.5,取上述算法的初始化主要包括端元数目估计和对矩阵A进行初始化两部分。本文采用OSP算法估计端元数目p,端元矩阵A可以采用随机从高光谱图像数据中选择p个像元光谱进行初始化。
求解过程采用投影梯度算法以加速式(6)的迭代,具体方法是将式(6)分解为两个子问题来求解,每个子问题固定A(或S)对S(或A)进行更新:

迭代过程可以采用最大迭代次数、误差阈值、用户交互等作为终止条件,本文采用相邻两次迭代目标函数值的比值小于某个阈值0.99的方法来实现算法的终止。
3 实验
实验采用Cuprite地区的AVIRIS数据进行光谱解混实验(如图2),AVIRIS数据包含224个波段(波长范围为400~2 500 nm),是一种高质量、低噪声的高光谱数据。这里我们选取其中50个连续的波段(1 978~2 478 nm)的图像进行算法的验证。
首先利用OSP方法估算出端元的个数,实验中设置迭代终止条件C<0.01,最终估算出有9个端元。
利用本文提出的改进的最小体积约束MVC-NMF算法对整幅图像进行光谱解混,图2显示了解混后得到的地表矿物的丰富分布图。与Swayze和Clark等人已经给出的该地区真实地物的分布报告[11]相比较,可确定这些端元各自对应的矿物。这说明本文所提出的算法基本反映了此区域的地物分布状况。

图1 Cuprite地区的AVIRIS数据假彩色合成图Fig.1 False-color image ofAVIRIS data in Cuprite
为了进一步比较,我们将美国地质调查局(United States Geological Survey,USGS)库中的对应矿物光谱作为参考光谱,将参考光谱在相应的波段范围内能量求积分,转换为光谱向量,并求取解混所得的端元与它们之间的光谱角,如表1所示。
从表1可以看出,用本文方法解混后所得的端元与USGS光谱库中的标准光谱相似度较高,总体上优于顶点成分分析(vertex component analysis,VCA)方法所提取的端元光谱。

表1 所提取的端元与USGS光谱库中标准光谱之间的光谱角Tab.1 The SAD between endmembers extracted and the standard spectrum

图2 不同矿物的丰度分布图Fig.2 Abundance maps of different minerals
4 结论
本文提出了一种基于OSP和NMF方法的高光谱混合像元分解方法。首先用OSP方法估计图像中端元的个数,从而更合理的对NMF算法进行初始化;针对MVC-NMF算法中单形体体积计算公式较为复杂而且需要降维的情况,提出了一种简单的单形体体积的计算方法作为约束条件构建NMF的目标函数。实验结果表明该方法解混效果跟实地调查报告分布情况基本吻合。
[1]贾森.非监督的高光谱图像解混技术研究[D].杭州:浙江大学,2007.
[2]张良培,张立福.高光谱遥感[M].武汉:武汉大学出版社,2005:15-18.
[3]钱乐祥,泮学芹,赵芊.中国高光谱成像遥感应用研究进展[J].国土资源遥感,2004,7(2):1-6.
[4]KESHAVAN,MUSTRAD J F.Spectral unmixing[J].IEEE Signal Processing Magazine,2002,19(1):44-57.
[5]JIA S,QIAN Y.Constrained nonnegative matrix factorization for hyperspectral unmixing[J].IEEE Trans.Geocsi.Remote sens.,2009,47(1):161-173.
[6]LIU X,XIA W,WANG B,ZHANG L.An approach based on constrained nonnegative matrix factorization to unmix hyperspectral data J].IEEE Trans.Geocsi.Remote sens.,2011,49(2):757-772.
[7]郑轶,蔡体健.稀疏表示的人脸识别及其优化算法[J].华东交通大学学报,2012,29(1):11-14.
[8]PAUCA V,PIPER J,PLEMMONS R.Nonnegative matrix factorization for spectral data analysis[J].Linear Algebra and Applications,2006,416(1):29-47.
[9]陈伟,余旭初,王鹤.基于OSP的端元个数估计方法[J].计算机工程,2009,35(24):280-281.
[10]MIAO L,QI H.Endmember extraction from highly mixed data using minimum volume constrained nonnegative matrix factorization[J].IEEE Trans Geosci Remote Sens,2007,45(3):765-777.
[11]SWAYZE G A.The hydrothermal and structural history of the cuprite mining district,southwestern Nevada:an integrated geological and geophysical approach[D].Boulder:University of Colorado,1997:399.

