高压直流输电系统的反馈线性化控制器设计及仿真
朱红萍,李白雅,李 燕
(湖南科技大学信息与电气工程学院,湖南湘潭411201)
高压直流输电(HVDC)在运行过程中会受到或小或大的扰动,如交流系统发生单相或三相短路故障,直流输电线出现短路故障,使系统的正常运行出现不稳定,直流输电系统的基本稳态调节特性为:整流侧由定电流特性和定α0特性,逆变侧由定 δ0特性和定电流特性组成[1-2]。HVDC系统内在的非线性使控制器的设计成为难点,整流侧和逆变侧的触发角对直流电流的变化率很敏感,当故障被清除时将导致直流电流和电压的振荡,这种振荡将会损坏换流阀[3-4]。本文提出一种简单的反馈线性化方法设计控制器,得到换流阀的触发角,用PSCAD/EMTDC软件仿真了在交流系统发生故障和受端是弱交流系统时的直流电流变化情况,结果表明了该控制器优于常规的PI控制器。
一 HVDC系统模型
一个两极的6脉动换流器组成的HVDC系统如图1所示。
由图1得到直流电流Id的表达式为
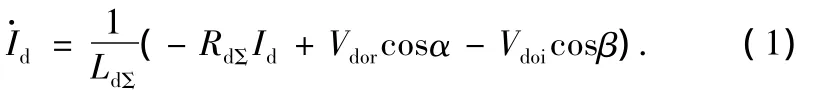

图1 直流输电系统模型
式中:LdΣ表示直流输电线路的等值电感和,RdΣ表示直流输电线路的等值电阻和,Vdor表示整流器的理想空载直流电压,Vdoi表示逆变器的理想空载直流电压,α表示整流器的触发滞后角,β表示逆变器的触发越前角。如果将式(1)进行变换:,则可以用下式表示直流电流方程:
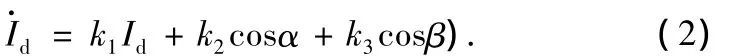
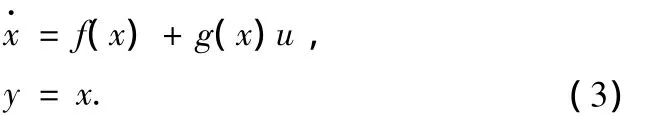
可以把系统看成是伪线性的,反馈线性化控制器为
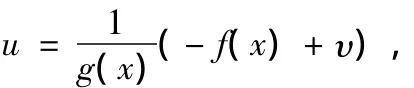

对于HVDC系统,α的计算可以表示如下:
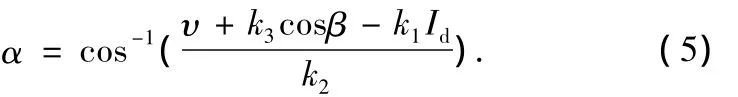
令系统的跟踪误差e=Idref-Id,Idref为电流参考值,为了保持Id为常数,跟踪误差e用PID调节器调节,用下式表示为
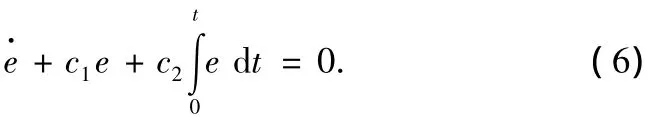
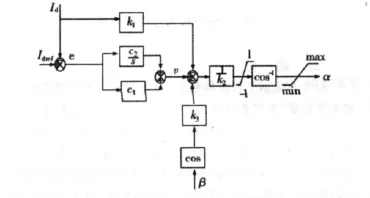
图2 整流器的α控制器
c1,c2的取值都是大于0的数,可以根据PI的经验取值,k1,k2,k3的值用 BP 算法来估算。cosα,cosβ,Id作为神经元的输入,k1,k2,k3作为神经元的网络权值,是神经元的输出[5]。其模型用图3表示。
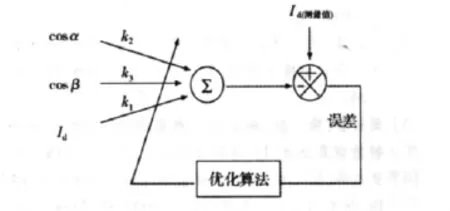
图3 神经网络模型
为了训练神经网络,直流输电系统采用常规的PI控制器,得到的测量值,β从逆变器测量得到。
二 算例仿真
为验证本文的反馈线性化控制器的优越性,在PSCAD/EMTDC的HVDC实例中进行了仿真分析,直流系统采用GIGRE HVDC BENCH MARK MODEL,将本文的反馈线性化控制器作为整流器的控制器,逆变侧的β控制器,γ控制器采用原系统的控制器,对系统的运行进行了仿真。系统整流侧参数:变压器为500 kV,1 000 MW,采用12脉波整流,线电压为 345 kV,SCR=2.5@84.0deg,直流电压为0.89PU;逆变侧的参数:变压器为500 kV,1 000 MW,采用12脉波整流,线电压为 230 kV,SCR=2.5@75.0 deg。整流器的 α 控制器的参数:c1=70,c2=1,k1,k2,k3的值由神经网络优化决定。αmin=0.087 3 rad,αmax=2.7 rad。逆变侧的β控制器,γ控制器采用HVDC实例中的参数。图4对整流侧交流母线发生单相接地故障进行了仿真(在0.3 s发生故障,持续0.05 s),图5对整流侧交流母线发生单相接地故障进行了仿真(在0.3 s发生故障,持续0.05 s),图6对逆变侧交流母线发生单相接地故障并同时改变SCR进行了仿真(在0.3 s发生故障,持续0.05 s),图7对逆变侧发生直流短路故障进行了仿真(在0.3 s发生故障,持续0.05 s),图8是采用BP时的适应值收敛曲线。
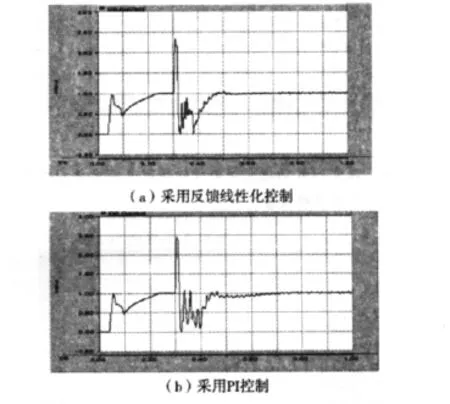
图4 在两种控制器下逆变侧发生单相短路时的直流电流波形对比
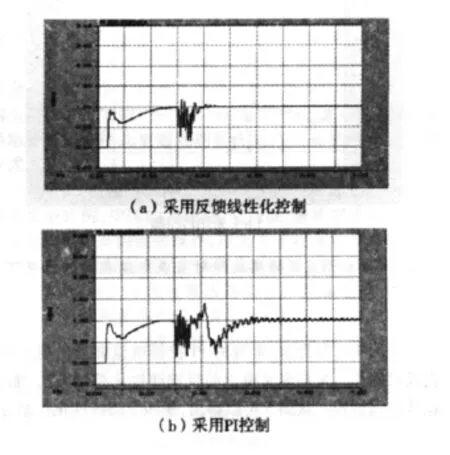
图5 在两种控制器下整流侧发生单相短路时的直流电流波形对比
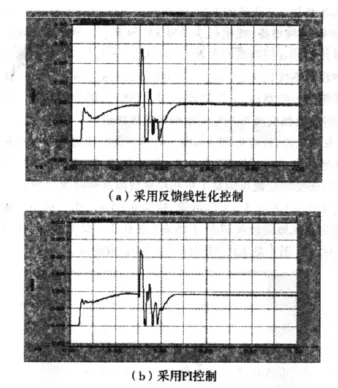
图6 改变SCR的逆变侧单相短路时直流电流在两种情况下的波形
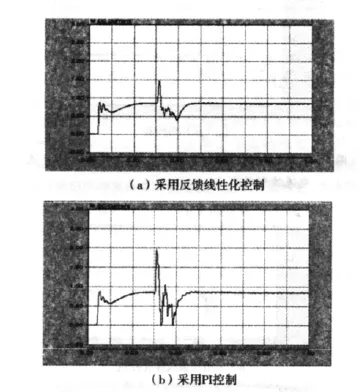
图7 逆变侧直流短路故障时直流电流在两种情况下的波形
从图4可以得出,常规的PI控制电流波形出现多峰,振荡时间长。采用本文提出的反馈线性化控制方法,能使振荡时间缩短。从图5可以得出,采用反馈线性化控制方法能使振荡减少,稳定时间缩短。图6采用常规的PI控制,出现超调大,多峰的现象,反馈线性化控制方法改善了这种缺点。图7反映了改变逆变侧的SCR,常规的PI控制,系统更易发生振荡。
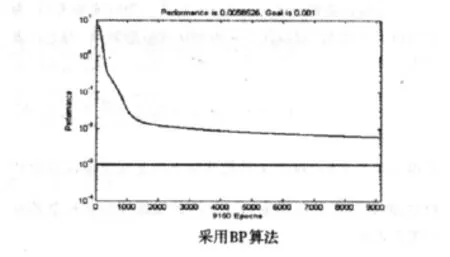
图8 fitness的变化过程曲线
三 结语
对于直流输电系统的稳定运行,设计一个合适的控制器非常重要,尤其在系统发生故障时,如何快速稳定直流电流。本文提出的反馈线性控制器对整流器触发角的控制,在一个非线性系统中消除了非线性,使其成为一个伪线性的系统,具有线性系统的形式。PI控制器和反馈线性化控制应用于直流输电系统发生短路故障,直流电流的变化情况运用PSCAD/EMTDC进行了仿真,可以得出结论:反馈线性化控制器使直流电流的振荡减少,恢复时间缩短,系统的鲁棒性更好。
[1]戴熙杰.直流输电基础[M].北京:水利电力出版社,1990.
[2]张跃锋,颜 伟,朱蕾蕾.交直流混合输电系统的换流变压器分接头控制[J].中国电力,2008,41(4):20-24.
[3]周长春,徐 政.联于弱交流系统的HVDC故障恢复特性仿真分析[J].电网技术,2003,27(11):18-21.
[4]黄志岭,田 杰.基于详细直流控制系统模型的EMTDC 仿真[J].电力系统自动化,2008,32(2):45-48.
[5]张德丰.Matlab神经网络应用设计[M].北京:机械工业出版社,2009.
[6]周孝法,陈 陈,宋正强,等.基于改进 PSO算法的HVDC PI控制器优化设计[J].高电压技术,2009,35(2):408-413.
[7]胡 江,魏 星.基于自适应粒子群算法的直流输电PI控制器参数优化[J].电网技术,2008,32(2):71-74.

