高气液比气井临界携液气流量计算新模型

周舰，王志彬，罗懿，李颖川，李璇

（1.中国石化华北分公司工程技术研究院，河南郑州 450006；2.西南石油大学石油工程学院，四川成都 610500）

高气液比气井临界携液气流量计算新模型

周舰1，王志彬2，罗懿1，李颖川2，李璇1

（1.中国石化华北分公司工程技术研究院，河南郑州 450006；2.西南石油大学石油工程学院，四川成都 610500）

基于气井井筒积液对气藏开发的危害性，在现有携液模型的基础上，利用受力平衡理论和能量守恒原理，建立了气井临界携液气流量计算新模型；通过引入新模型系数，对液滴大小及液滴变形特征进行了综合表征。模型计算结果表明，新模型系数随压力增大而增大，有效地弥补了现有携液模型存在的不足。现有携液模型及新模型的适应性分析结果表明，新模型在高、低压气井中均具有良好的适用性。现场应用新模型有效预测了大牛地气田气井的积液状态，为产水气藏的有效开发提供了有力的技术支持。

产水气藏；高气液比；临界气流量；携液模型；液滴变形；临界韦伯数

0 引言

大牛地气田属特低渗透致密砂岩产水气藏，具有低孔、低渗、低压、低产等特点。在开发过程中，气井积液致使井底回压增加，产量下降甚至停产，对气藏的危害十分突出[1-3]。2009年以来，大牛地气田的气井压力逐年降低，积液井逐年增多。至2012年底，泡排井已达到819口，占总井数的76.9%，气井积液现象已非常严重。准确预测气井的临界携液气流量，及时判断气井积液状况，对优化气井工作制度、优选排水采气工艺、有效排除井筒积液具有重要意义。

目前，在气井临界携液气量的预测模型中，Turner和Coleman圆球模型[4-5]是在将韦伯数设为定值30，并假设液滴为圆球状的条件下建立的，没有考虑最大液滴尺寸的差异和液滴变形的影响；李闽（Li）椭球模型[6-7]和王毅忠（Wang）球帽模型[8]虽然考虑了液滴的变形，但没有考虑最大液滴尺寸差异。上述模型在大牛地气田产水气井中的应用效果较差，判断积液的准确率低于70%。为此，本文在同时考虑液滴变形和最大尺寸差异的影响下，进行了气井临界携液模型的研究。

1 气井临界携液新模型

1.1 物理模型

在井底流压为p，气相流速为u的情况下，以单个液滴为研究对象，忽略液滴间的碰撞与合并，以及液滴与气流间的传热与传质，则液滴所受的力有重力FG、气流对液滴的曳力FD和浮力FB。在这些力的作用下，液滴发生变形。

假设:1）在液滴变形过程中，其表面的压力分布满足Flachsbart规律，受力方向指向球面表示液滴受到滞止压力作用向内挤压，背离球面表示液滴受到抽吸作用向外拉伸（见图1a）；2）液滴变形后为规则椭球状，迎风面为圆形，椭球表面光滑；3）液滴的变形量以水平面对称分布，θ相同的微元面的径向位移量Δh相同（见图1b）。

图1 液滴受力物理模型

1.2 数学模型

设圆球状液滴的初始直径为d0，发生变形后形成的椭球状液滴的迎风面直径为d，高为h；与液滴竖直方向夹角为θ的微元面面积为A（θ），承受的压力为Δp（θ），产生的径向位移量为Δh（θ）。

根据液滴受力情况进行分析得出[9]，当气相流速足够大时，液滴将悬浮在气流中，此时重力等于浮力与曳力之和，即

式中:CD为曳力系数；AP为液滴迎风面面积，m2；ρG为气体密度，kg/m3；ucr为临界气流速，m/s；g为重力加速度，m/s2；ρL为液滴密度，kg/m3；V为液滴体积，m3。

假设液滴变形最大时，椭球状液滴的迎风面直径d是液滴初始直径d0的k倍，则式（1）可写为

式中:k为液滴的最大变形特征参数。

若气流能够将气井中的最大液滴带出井口，则井筒被视为能正常携液生产；因此，临界携液气流速应根据液滴的最大直径dmax进行计算，而液滴的最大直径可由临界韦伯数Wecrit确定，即

式中:σ为气液间的界面张力，N/m。

将式（3）代入式（2），得到椭球状液滴的临界携液气流速ucr及临界携液气流量qcr分别为

其中，Ck，Wecrit用以综合表征液滴的大小和液滴的变形特征，可表示为

式中:At为油管截面积，m2；T为温度，K；Z为p，T条件下气体的偏差系数。

可以看出，要计算气井临界携液气流量qcr，关键是计算临界韦伯数Wecrit、液滴变形特征参数k和气流对液滴的曳力系数CD。

1.3 参数计算

1.3.1 临界韦伯数

综合考虑气相流速和液相流速对液滴尺寸的影响，选择Azzopardi方法[10-11]计算临界韦伯数，计算表达式为

式中:WeL为液相的韦伯数；GLE为液相的质量流量通量，kg/（m2·s）。

1.3.2 液滴变形特征参数

忽略液滴与气流间的热质交换作用，根据能量守恒原理，则液滴从圆球状变为椭球状过程中的能量方程为

式中:ΔE为液滴的内能变化量，J；ΔW为液滴对外界所做的功，J。

液滴从圆球状变为椭球状后，表面积增加，表面能也增加。在变形过程中，将消耗液滴的内能，液滴内能的变化量等于表面能的变化量，即

式中:AS0，AS分别为圆球状及椭球状液滴的表面积，m2。

由于迎风面与背风面各处气体的流速分布不同，液滴与气流间的表面压差也不相同，最终液滴会产生变形而对外界做功。对整个液滴的表面进行积分，得到总功量ΔW为

Hinze等[12-13]研究发现，在液滴变形过程中，其表面的压力分布满足Flachsbart规律，即

由于液滴变形前后的体积相等，即πd2h/6=πd03/6，由此可得椭球体的高度h=d0/k2，则液滴在变形过程中的微元面径向位移量Δh（θ）可表示为

椭球状液滴的表面积AS可表示为

将式（11）—（13）代入式（10），并结合临界韦伯数的定义，可得

式（14）为液滴变形特征参数k与Wecrit的函数关系式，可以看出，k仅受临界韦伯数的影响。

1.3.3 曳力系数

Liu等[14]研究发现，扁平体的曳力系数是圆球体的3.632倍，而刚性椭球体的曳力系数介于扁平体与圆球体之间。考虑到液滴在气流作用下发生内部流动，使得液滴的曳力系数比刚性椭球体的小，根据Helenbrook&Edwards方法[15]，对刚性椭球体的曳力系数进行修正，得到椭球状液滴的曳力系数表达式为

将式（6），（7），（14），（15）代入式（4），即可得到气井的临界携液气流速，它受临界韦伯数Wecrit和变形特征参数k及曳力系数CD的影响。由于曳力系数CD是液滴变形特征参数k的函数，而k又是临界韦伯数Wecrit的函数；因此，只要知道液滴的临界韦伯数，采用试错数值逼近法求解式（4）、式（5），即可得到液滴的临界气流速和气流量。

2 新模型与现有模型对比分析

2.1 压力影响分析

设油管内径为62mm，井口温度为15℃，水流量为1m3/d，天然气的相对密度为0.6。利用新模型计算不同井底流压下的临界韦伯数得到关系曲线（见图2）；应用各种模型计算不同井底流压下的关系式系数得到关系曲线（见图3）。

由图2可以看出，利用新模型计算得出的临界韦伯数受压力影响较大，变化范围在2.5～60.0，压力越大，临界韦伯数越大。由图3可以看出，新模型的关系式系数并非是一个常数，而是在2.92～5.10之间变化，且随压力增大而增大，弥补了现有模型将关系式系数取为定值的缺陷。

图2 液滴临界韦伯数与压力关系曲线

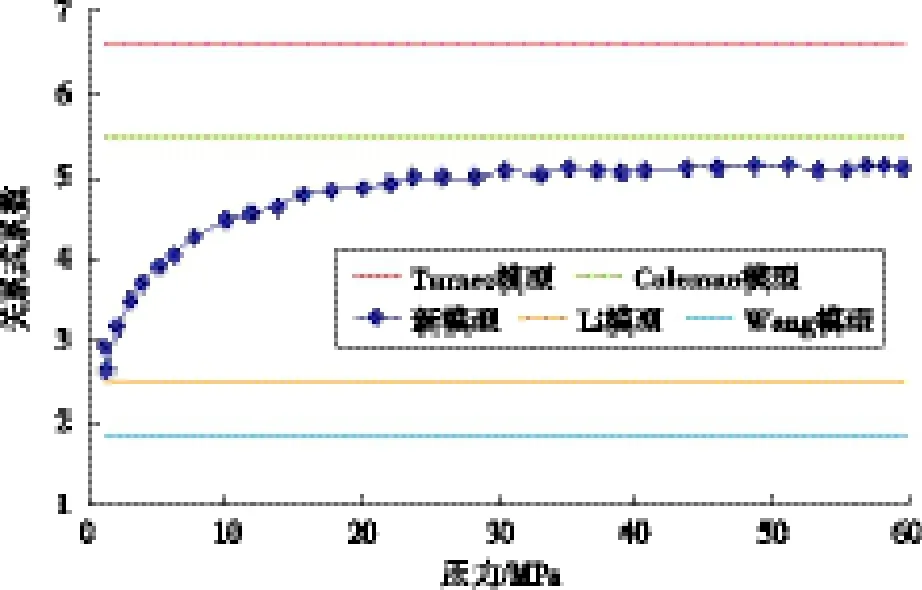
图3 不同模型关系式系数与压力关系

利用各种携液模型计算不同井底流压条件下的临界携液气流量（见图4），可以看出，压力越大，气井的临界携液气流量越大，新模型计算得到的的临界携液气流量值介于Coleman模型与Li模型计算值之间。

2.2 低压气井的适应性分析

以Coleman发布的低压气井的试验数据[2]（井口油压为0.26～3.41MPa）为基础，分别利用现有的携液模型及新模型，计算不同井底流压条件下的临界携液气流量（见图5），将其与Coleman测试值进行对比，以评价各模型在低压气井的适应性。

由图5可以看出，利用Turner和Coleman模型计算得出的临界携液气流量比实测值偏大，Li，Wang模型的计算值偏小，而实测值均匀分布在新模型计算值的两侧，说明新模型的计算值与实测值吻合较好，在低压气井具有较好的适用性。

图4 不同模型的临界携液气流量与压力关系

图5 低压气井临界携液气流量模型计算值与测试值对比

2.3 高压气井的适应性分析

以Turner发布的高压气井试验数据[1]（井口油压为5～56MPa）为基础，分别利用现有模型及新模型，计算不同井底流压条件下的临界携液气流速，并将其与积液井、未积液井的气流速测试值进行对比（见图6）。可以看出，Turner，Coleman模型和新模型在高压气井具有较好的适应性，能较准确地判断高压气井的积液状态，符合率均达85%以上，而Li，Wang模型的临界携液气流速计算值偏小，符合率较低。

图6 高压气井临界携液气流速模型计算值与测试值对比

3 现场应用

大牛地气田的230口典型直井中，积液井124口，接近积液井33口，未积液井73口。将模型计算的230口井临界携液气量与实际产气量对比（见图7）。结果显示:积液井127口，接近积液井44口，未积液井59口。而与实际对比可知，模型共误判了28口，准确率为87.8%，表明新模型在大牛地气田具有良好的适应性。

图7 模型计算值与实际值对比

4 结论

1）在综合考虑液滴尺寸差异和液滴变形特征的前提下，引入系数Ck，Wecrit，建立了临界携液气流量的计算新模型。新模型系数变化范围在2.92～5.10，随压力增大而增大，弥补了现有模型系数为定值的缺陷。

2）携液模型适应性评价结果表明，新模型在低压、高压气井中均具有较高的准确性，扩大了现有模型的适用范围。

3）现场应用表明，新模型在大牛地气田具有较好的适用性，判断气井积液状态的符合率达到87.8%，为判断气井积液提供了一种新方法和新思路。

[1]刘志森.塔河凝析气井井筒积液判断标准[J].断块油气田，2009，16（3）:68-70.

[2]曹光强，周广厚.动能因子-积液高度法诊断气井积液[J].断块油气田，2009，16（6）:123-125.

[3]栾国华，何顺利，舒绍屹，等.应用人工神经网络方法预测气井积液[J].断块油气田，2010，17（5）:575-578.

[4]Turner R G，Hubbard M G，Dukler A E.Analysis and prediction of minimum flow rate for the continuous removalof liquids from gaswells [J].JPT，1969，21（9）:1475-1481.

[5]Coleman SB，Clay H B，Mccurdy DG，etal.A new look at predicting gas-well load up[R].SPE 20280，1991.

[6]Li Min，Sun Lei，Li Shilun.New view on continuous removal liquids from gaswells[R].SPE 70016，2001.

[7]李闽，郭平，刘武，等.气井连续携液模型比较研究[J].断块油气田，2002，9（6）:39-41.

[8]王毅忠，刘庆文.计算气井最小携液临界流量的新方法[J].大庆石油地质与开发，2007，26（6）:82-85.

[9]雷登生，杜志敏，单高军，等.气藏水平井携液临界流量计算[J].石油学报，2010，31（4）:637-639.

[10]Jepson D M，Azzopardi B J，Whalley P B.The effect of gas properties on drops in annular flow[J].International Journal ofMultiphase Flow，1989，15（3）:327-339.

[11]Azzopardi B J，Pierarcey A，Jepson D M.Drop sizemeasurements for annular two-phase flow in a 20 mm diameter vertical tube[J]. Experiments in Fluids，1991，11（2）:191-197.

[12]Hinze JO.Critical speeds and sizes of liquid globules[J].Applied Scientific Research，1949，1（1）:273-288.

[13]W ierzba A.Deformation and breakup of liquid drops in at nearly criticalWebernumbers[J].Experimentsin Fluids，1990，9（1）:59-64.

[14]Liu Z，Reitz R D.An analysis of the distortion of the distortion and breakup mechanisms of high speed liquid drops[J].International JournalofMultiphase Flow，1997，23（4）:631-650.

[15]Helenbrook B T，Edwards CF.Quasi-steady deformation and drag of uncontaminated liquid drops[J].International Journal of Multiphase Flow，2002，28（10）:1631-1657.

（编辑 刘文梅）

New model to calculate critical liquid-carrying gas flow rate in gaswellw ith high gas-liquid ratio

Zhou Jian1,W ang Zhibin2,Luo Yi1,Li Yingchuan2,Li Xuan1

(1.Research Institute of Engineering and Technology,Huabei Com pany,SINOPEC,Zhengzhou 450006,China; 2.School of Petroleum Engineering,Southwest Petroleum University,Chengdu 610500,China)

As liquid loading in gaswell will bring serious damage to the development of gas reservoir,a new model to predict the critical liquid-carrying gas flow rate has been established with liquid-droplet force equilibrium theory and energy conservation princip le based on the currently used liquid-carryingmodels.The new coefficient is introduced into themodel to comprehensively characterize the droplet size and deformation characteristics.The calculation results of the model show that the new model coefficient,becomes larger with the increase of pressure,which compensates the defects of the currently used liquid-carrying models.Adaptability analysis results of the newmodel and the currently usedmodels show that the newmodelhashigh accuracy in both low and high pressure gas wells.The new model is applied to effectively predict effusion status in Daniudi Gas Field.It providesa strong technicalsupport for theeffective developmentofwater-produced gas reservoir.

water-produced gas reservoir;highgas-liquid ratio;criticalgas flow rate;liquid-carryingmodel;liquid-dropletdeformation; criticalWebernumber

中石化华北分公司科研项目“东胜气田钻采工程工艺体系优化研究”（QTKF-2012-15）

TE37

A

2013-05-16；改回日期：2013-09-22。

周舰，男，1989年生，工程师，硕士，现从事采油、采气工艺研究工作。E-mail:zhoujian860810@126.com。

周舰，王志彬，罗懿，等.高气液比气井临界携液气流量计算新模型[J].断块油气田，2013，20（6）:775-778，796.

Zhou Jian，Wang Zhibin，Luo Yi，et al.New model to calculate critical liquid-carrying gas flow rate in gas well with high gas-liquid ratio [J].Fault-Block Oil&Gas Field，2013，20（6）:775-778，796.

10.6056/dkyqt201306024