一种基于SVDD模型的说话人确认方法研究

陈觉之，张贵荣，周宇欢

(1.海军指挥学院信息系，江苏 南京 211800;2.中国人民解放军92601部队计量站，广东 湛江 524009;3.解放军理工大学指挥信息系统学院，江苏 南京 210007)

0 引言

基于概率统计方法的高斯混合模型(GMM)在说话人识别中可以获得较好的性能，特别在闭集条件下，说话人辨认的准确率已经相当高。但是，当进行说话人确认或在开集条件下进行说话人辨认时，性能下降明显，这是因为对于GMM模型，确认阈值的设定是一个较难解决的问题。GMM模型的确认阈值是通过实际测试并采用经验的方法设定，对于不同的数据集，阈值需要通过实验反复调整。由于基于GMM模型的识别方法的似然得分会随着测试数据的不同而有很大的变化，因此在设定阈值时，一般还需要先对得分进行规整。目前流行的方法是利用大量不同说话人的语料建立一个统一的背景模型(UBM)[1]，将测试说话人的得分减去在统一背景模型中的得分后再进行判决。但是，统一背景模型的训练需要大量的语料，训练的时间很长，而且相对比较固定，不易根据环境做自适应变化，因此有待进一步改进。另外一种得分规整的方法[2]是将每个说话人模型得分的几何平均值作为参考进行得分规整，这种规整方法与具体的训练集合有关，同时也与当前测试语音相关，因此有很大的灵活性。然而这种方法仍然是基于概率统计方法的，似然得分的准确性与训练和测试的语料有关，当语料不充分时，性能会大大降低。

本文引入区分性模型进行说话人确认，试图弥补概率统计模型的缺陷。区分性模型从考虑类别的边界出发，利用优化方法寻找区分样本的最优分界面。支持向量机(SVM)是目前应用最广泛的区分性模型，但是SVM也存在一定的缺陷，在反类数据难以获得或类别不平衡时，其识别性能会大打折扣，例如计算机的登录系统，往往只能获得机主或少数几个人的语音信息，反类信息难以获得和确定，此时基于单分类的区分性模型可以有效解决这一问题。

SVDD[3]是一种单分类区分性模型，与 SVM不同，它的分类界面不再是超平面，而是一个包含全部个体的超球面，因此在只有少量反类数据，甚至没有反类数据时也能实现对目标类的识别。另外，由于SVDD的边界可以在训练时通过调整惩罚因子和核参数来控制，因此相比GMM模型，确认阈值的设定更加简便[4-5]。

本文根据说话人语音和SVDD模型的特点[6]，改变传统SVDD模型硬判决的方式，采用以样本接受率为指标的软判决方法[7]，提高了说话人确认系统的识别率和鲁棒性。

1 SVDD理论简介

SVDD是Tax在SVM的基础上提出的一种单分类器算法[8]。SVDD的基本思想是:通过核函数将输入空间映射到一个高维空间，并在这个高维空间构造一个包含所有训练样本点的最小球体，在球面上的样本点即为SVDD的支持向量。

假设有一类紧密的有界数据集f(x)，可以借助一个球心为a和半径为R的超球体包含并描述它。由于训练样本中一般含有噪声或野值，为提高结果的鲁棒性，对每个样本引入松弛变量ξi≥0，∀i，这样就得到包含大多数目标类训练样本的超球体，其目标函数为:

其中n是数据集中样本的总数，C是正则化参数，约束条件为:

利用Lagrangian函数求解上述约束下的最小化问题，当输入空间的样本点不满足球状分布时，可以通过核方法把输入空间先映射到高维空间，然后在映射后的高维空间内求解，也就是将内积运算变换成核函数形式:

其中φ为非线性映射，引入核函数后，Lagrangian函数形式如下:

约束为:

假设z为测试样本，当满足式(6)时，相当于z落在该超球体内部，即判z是正常类，否则为异常类。

综上所述，SVDD属于基于支持向量的单分类技术，它利用核方法提升非线性分类能力，可以解决实际应用时小样本或样本不平衡的问题。

核函数对SVDD的性能影响较大，目前比较常用的核函数有3 种[9]:

(1)多项式函数:

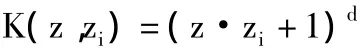
(2)高斯函数:

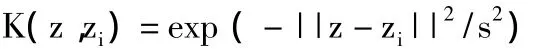
(3)Sigmoid函数:

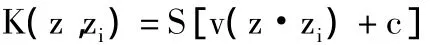
本文将研究不同核函数下说话人确认系统的性能，并选择最优的核函数作为最终仿真实验时SVDD的核函数。

2 基于SVDD模型的说话人确认系统

基于SVDD模型的说话人确认系统分为训练和测试两个阶段，其流程如图1所示。

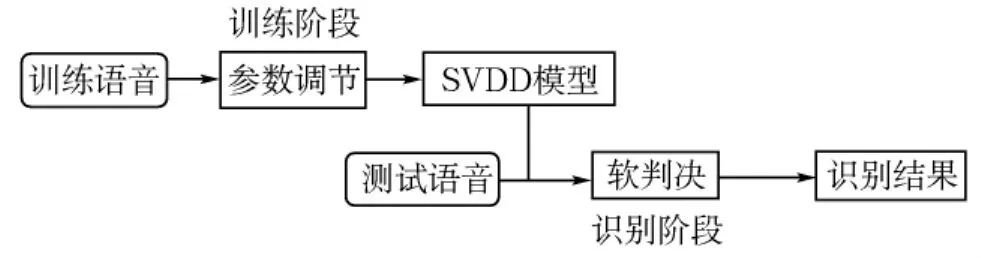
图1 基于SVDD模型的说话人确认系统流程图

训练阶段需要考虑3部分内容:说话人语音特征、惩罚因子和核函数参数，其中后两种参数的调节对SVDD模型至关重要。

惩罚因子C对分界面的影响很大，其值越大，表示样本被拒绝的代价越高，因此被拒绝的样本数量越少，分界面容积越大。不同的核函数需要调节的参数不同，现以高斯核函数[10]为例，介绍核参数对分界面的影响。高斯核函数中只有一个参数s需要调节，s越大，分界面越平滑，被选中的支持向量越少，分界面的容积也越大;相反分界面会越紧致，由于紧贴样本点，分界面的容积较小，形状较曲折。如图2所示，参数C从上到下增大，参数s从左到右增大。

图2 惩罚因子和核函数参数对分界面的影响

测试阶段是将需要测试的说话人语音特征，输入到相应的说话人SVDD模型，并与确认阈值比较，得到最终的判决结果。测试阶段最主要的问题是样本类别的判决方式。传统的方法是比较样本到球心a的距离与半径R的大小，如果小于R则判决样本属于该模型。但是Mel频率倒谱系数(MFCC)[11-12]和线性预测编码(LPC)等语音特征中不仅包含了说话人信息，同时也包含了语义、情感等信息，因此不同说话人的MFCC和LPC在特征空间上的分布是交织的，传统方法的正确率并不高。考虑到说话人语音特征这一实际特性，可改变传统硬判决方式，采用样本接受率为最终判决依据[13]。

设测试语音Stest的测试样本数为N，单个样本仍然用传统方法判决，设被接受的样本个数为S，定义该模型的样本接受率为:Rscore=S/N，此时Rscore∈[0，1]，当测试语音的样本接受率Rscore=1时，表示测试语音属于该模型;当Rscore=0时，表示测试语音不属于该模型;当Rscore∈(0，1)时，其值反映了测试语音属于该模型的程度。因此最终的判决条件为:

其中，T为确认阈值。确认阈值可以是所有模型统一设定，也可以各个模型单独确定，相比而言，后者的等错识率(EER)会低一些，这是因为SVDD模型的训练是分别进行的，各模型的训练样本不同，导致SVDD模型的形状和半径也不同，因此各模型的最优确认阈值也不相同。

3 SVDD核函数选择与参数调节

本节主要通过实验选取最优的核函数，并通过网格搜索方法调节惩罚因子和核参数，使基于SVDD模型的说话人确认系统性能达到最优。

3.1 不同核函数下SVDD模型性能比较

实验固定惩罚因子C为0.01，分别调节多项式核函数和高斯核函数的参数，其等错识率的变化分别如表1和表2所示。多项式核函数主要调节核的阶数d，实验中d从1到3变化。

表1 基于多项式核函数的SVDD等错识率随参数的变化

高斯核函数主要调节核的宽度s，实验中s从0.3到3变化。

表2 基于高斯核函数的SVDD等错识率随参数的变化

表1和表2显示了两种核函数在不同核参数下的等错识率，可以看出，基于高斯核函数的性能总体较好。因此SVDD模型选取高斯核函数。

3.2 采用网格搜索方法选取模型参数

在模型训练中，一个最重要的问题是调节惩罚因子C和高斯核参数s，使得系统性能最优[14]，本文采用网格搜索(grid-search)方法，首先固定惩罚因子C，调节高斯核参数s，得到较优的高斯核参数;接着固定高斯核参数s，调节惩罚因子C，得到较优的惩罚因子，最后在较优的(C，s)附近搜索，从而得到最终的(C，s)。表3显示所有模型统一设定阈值条件下，SVDD模型的等错识率。

表3 统一设定阈值条件下的EER

由表3 看出，SVDD 模型在 C=0.007 ～0.003，s=0.3～0.6范围内，等错识率变化不大，大多数都分布在0.071 ～0.057 之间，而当 C=0.004，s=0.5 时，EER=0.0571。

表4 单独设定阈值条件下的EER

表4考虑分别设置各SVDD模型的确认阈值，可以看到，分别设定阈值后，等错识率均有所下降，分布范围在0.057 ～0.045 之间，而在 C=0.003，s=0.4时，等错识率最低，为0.045。

4 仿真实验结果及分析

为了检验算法的识别性能，对算法进行计算机仿真实验，并与基于GMM模型的算法性能进行比较。实验中语音数据库为TIMIT，选用其中50人，每个人有20句语音，长度均为2秒。训练和识别分别选不同的10句。所有的语音均为16kHz采样，16位精度，按帧提取13维MFCC和16维LPC特征参数，帧长和帧移均为16ms。

本文采用交叉验证法，每次选取一个说话人的语音作为正类样本，其余49人的语音作为反类样本，并取50次实验的平均等错识率作为系统性能的评价标准。实验分别在训练样本充分、训练样本不充分和有反类数据3类训练条件下进行。

4.1 训练样本充分条件下

GMM模型的调节参数主要是混合度M，本文试验了一系列M值，取最优结果与SVDD模型比较。本节试验了在20s训练语音条件下两模型的性能，结果如表5所示。

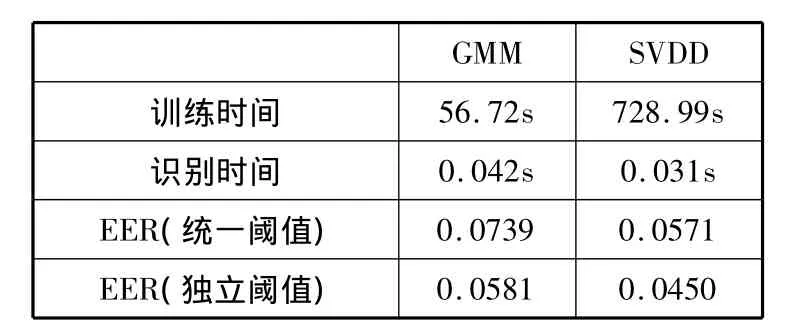
表5 GMM与SVDD比较(20s训练数据)

表5显示当训练样本充分时，SVDD的训练时间较长，这是因为SVDD的训练过程就是搜索支持向量的过程，其计算时间随样本数目呈幂次增长，当训练样本的数目较多时，训练时间较长。而识别时，由于只需计算样本到球心的距离，因此识别时间SVDD更占优势，同等条件下相比 GMM识别时间减少了26.2%;等错识率无论是在统一设定阈值还是单独设定阈值条件下，与GMM相比都低近23%。

4.2 小样本训练条件下

本文在小样本训练条件下，重复了前面的实验。在模型训练时仅选用2秒的语音作为训练样本，分别比较了两模型在统一设定阈值和单独设定阈值的性能。

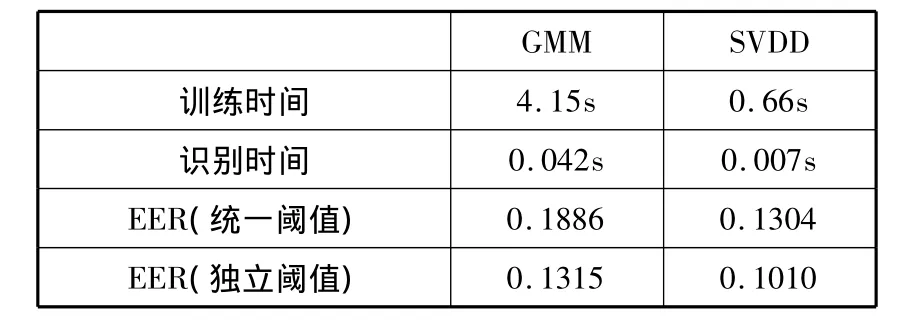
表6 GMM与SVDD比较(2s训练数据)

从表6可以看出，在训练样本不足条件下，两模型的等错识率都有所增加，但是SVDD的等错识率仍然较低，且两者差距更加明显，体现了SVDD在小样本训练条件下的优势。统一设定阈值条件下，SVDD的EER比GMM低31%，单独设定阈值条件下，EER低23%。另外，在小样本条件下，由于训练样本减少，SVDD的训练时间迅速减少，其训练时间和识别时间都只有GMM模型的1/6左右，更加满足实时处理的要求。

4.3 反类样本参与训练条件下

本文还比较了SVDD有反类数据参与训练时两类模型的性能。GMM模型采用20秒的训练数据，全部是正类样本，而SVDD模型采用10秒的正类数据和588个反类样本(相当于10秒语音)训练，反类数据随机从另外的49人中选取。

从表7可以看出，在反类样本参与训练时，虽然正类训练样本只有GMM模型的一半，但SVDD模型的误识率依然较低。统一设定阈值条件下，SVDD的EER比GMM低18.94%，单独设定阈值条件下，EER低8.95%。因此，在无法获得更多正类样本时，增加反类样本可以继续提升SVDD的性能，这一特点在实际应用中也是非常有用的。

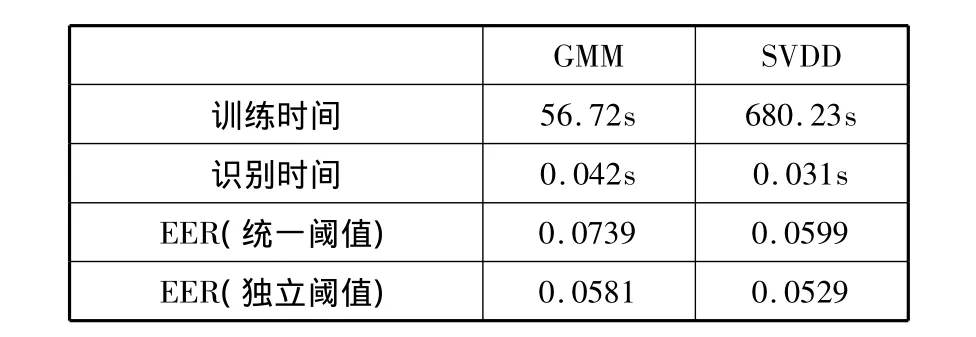
表7 GMM与SVDD比较(SVDD有反类训练样本)

从表5、表6、表7所显示的3种不同训练条件下对基于SVDD和GMM模型的说话人确认方法仿真对比数据可以看出，前者有比较明显的优势，特别是在小样本训练条件下尤为突出。

5 结束语

GMM模型的似然得分易随测试条件变化，导致其确认阈值较难设定。本文引入区分性模型SVDD进行说话人确认，并结合语音中各种信息混杂的特点，设计出软判决方式，提高了说话人确认的鲁棒性和识别率。实验显示，在训练样本充分和小样本训练条件下，SVDD的识别时间和识别率都较GMM更优，而在缺少正类样本情况下，通过增加反类样本依然可以提升SVDD的识别性能。

SVDD模型中(C，s)的选取是比较繁重的工作，目前是采用格型搜索的方式，遍历最优参数可能出现的区域，虽然可以利用先验的知识减少一定的搜索范围，但总体上还是十分耗时的。因此，下一步考虑引进遗传算法等全局性算法，使得参数选取的计算时间更少和准确性更高;实验过程中发现(C，s)与最终的确认阈值存在一定的关系，基于此可以进一步简化(C，s)的选取和阈值的设定过程。另外，实验显示，SVDD和GMM模型存在互补性，因此下一步将考虑融合两模型的优点进行说话人确认实验，以期得到更佳的识别性能。

[1] Reynolds D A，Quatieri T F，Dunn R B.Speaker verification using adapted Gaussian mixture models[J].Digital Signal Processing，2000，10(1-3):19-41.

[2] Sturim D E，Reynolds D A.Speaker adaptive cohort selection for Tnorm in text-independent speaker verification[C]//Proceedings of the 2005 IEEE International Conference on Acoustics，Speech，and Signal Processing.2005，1:741-744.

[3] Tax D M J，Duin R P W.Support vector data description[J].Machine Learning，2004，54(1):45-66.

[4] Banerjee A，Burlina P，Diehl C.A support vector method for anomaly detection in hyperspectral imagery[J].IEEE Transactions on Geoscience and Remote Sensing，2006，44(8):2282-2291.

[5] Banerjee A，Burlina P，Meth R.Fast hyperspectral anomaly detection via SVDD[C]//Proceedings of the 2007 IEEE International Conference on Image Processing.2007，4:101-104.

[6] Xin D，Wu Z，Zhang W.Support vector domain description for speaker recognition[C]//Proceedings of the 2001 IEEE Signal Processing Society Workshop on Neutral Networks for Signal Processing.2001:481-488.

[7] Tao X，Chen W，Du B，et al.A novel model of one-class bearing fault detection using SVDD and genetic algorithm[C]//Proceedings of the 2007 IEEE Conference on Industrial Electronics and Applications.2007:802-807.

[8] Tax D M J，Duin R P W.Support vector domain description[J].Pattern Recognition Letters，1999，20(11-13):1191-1199.

[9] Niu Q，Xia S，Zhou Y，et al.Fault condition detection based on wavelet packet transform and support vector data description[C]//Proceedings of the 2008 IEEE International Symposium on Intelligent Information Technology Application.2008，1:776-780.

[10] Bu H，Wang J，Huang X.A practical and robust way to the optimization of parameters in RBF kernel-based oneclass classification support vector methods[C]//Proceedings of the 5th International Conference on Natural Computation.2009:445-449.

[11] 甄斌，吴玺宏，刘志敏，等.语音识别和说话人识别中各倒谱分量的相对重要性[J].北京大学学报:自然科学版，2001，37(3):371-378.

[12] 杨大利，徐明星，吴文虎.语音识别特征参数选择方法研究[J].计算机研究与发展，2003，40(7):963-969.

[13] Guo L，Xiao H，Fu Q.Fuzzy recognition method for radar target based on KPCA and SVDD[C]//Proceedings of the SPIE，MIPPR 2007:Pattern Recognition and Computer Vision.2007，6788:15-17.

[14] Wang C，Ting Y，Liu Y.A novel approach of feature classification using support vector data description combined with interpolation method[C]//Proceedings of the 34th IEEE Annual Conference on Industrial Electronics.2008:1828-1832.