基于遗传算法的舰炮随动系统PID 参数整定
王茂林,张志华,武翰文
(1.辽宁葫芦岛市92941 部队,辽宁 葫芦岛 125001;2.海军驻连云港地区军事代表室,江苏 连云港 222006)
控制器参数整定的好坏主要影响控制系统的控制质量和鲁棒性等2 个方面。PID 控制器具有简单实用和对模型误差具有一定鲁棒性的特点,被广泛的应用到舰炮随动控制系统。对于控制系统的性能来说,PID 控制器参数优化设计和整定至关重要。以往的舰炮随动控制系统通常采用试凑的方法获取PID 控制器参数,这种方法往往带有“半经验”的色彩,首先根据经验公式或基于某些统计图表计算出控制器的初始参数,在用试验加试凑的方法调试PID 控制器参数以获得预期的控制性能[1]。这类方法耗时长,需要调试人员具有较高实际工作经验,且依赖于经验公式或统计数据,很难获取。
遗传算法(genetic algorithm)是一类借鉴生物界的进化规律(适者生存,优胜劣汰遗传机制)演化而来全局最优概率搜索方法。它是由美国的J. Holland 教授[2]1975 年首先提出,在Goldberg[3]给出遗传算法基本框架后在控制界引起广泛的兴趣,被广泛应用于控制领域,如系统辨识、PID 控制、最优控制、自适应控制、鲁棒控制和智能控制等。应用遗传算法进行PID 控制器参数优化整定的关键技术有2 个,一是有约束的优化空间,寻找适当的有约束的优化空间直接关系到优化的效率和结果,而控制器参数本身没有物理背景,很难确定其适当范围,考虑到控制器参数的优化设计目标是在保证控制系统稳定的情况下,控制系统同时还满足一定指标要求,因此本文采用广义Hermite-Biehler 定理确定优化空间;二是合理的目标函数,遗传算法是通过适应度函数值来衡量搜索效果,适应度函数是由目标函数转换而来,目标函数则反映实际的控制要求,因此目标函数是算法能否应用成功的关键,综合考虑控制系统的要求,控制偏差趋于零、较快的响应速度和较小的超调量,上升时间短,以误差泛函积分评价指标设计了目标函数。
1 舰炮随动控制系统建模
舰炮随动PID 控制系统结构框图如图1 所示,图中u(t)为控制输入,e(t)为误差信号,rin(t)为输入量,yout(t)为输出量。

图1 随动系统结构框图
取被控对象的传递函数为[4]

PID 控制器的传递函数为

式中:kp为比例系数;Ti为积分时间常数;Td为微分时间常数;
2 遗传算法整定PID 控制参数
2.1 问题描述
对给定的控制对象,寻找一组PID 控制器参数kp,ki,kd,使得被控系统误差泛函积分评价指标最小,计算误差泛函积分评价指标的函数为目标函数,适用度函数可由目标函数转换得到。
2.2 稳定域计算
在随动控制系统优化设计中,首先就要保证系统是稳定的。系统稳定域也就是对于确定的kp,ki,kd范围,闭环特征多项式为

式(3)是Hurwitz,也就是多项式的所有根在开左半平面。利用广义Hermite-Biehler 定理[5,6]计算控制系统的稳定域,可以得到kp,ki,kd范围:

2.3 目标函数选取及实现
目标函数反映实际的控制要求,过度过程的品质指标只有在零初始条件和单位阶跃给定输入下才有意义。当给定的信号不是单位阶跃函数,过度过程的品质指标就失去意义了。再有控制系统的输入也不一定是单一控制信号,还有其它干扰,因此需要建立一种更为一般的广义的品质指标评价函数,叫做性能指标积分评价,是以控制系统瞬时误差(e(t))函数为泛函的积分评价。
在众多的误差泛函积分评价指标中,究竟选择哪个是最佳的呢?文献[7]从上述性能指标的实用性(工程实用价值和运算是否方便)和选择性(参数变化引起指标变化越大越好)分析比较,认为时间乘以误差绝对值积分J(ITAE)=(ITAE)性能指标具有较好的实用性和选择性。因此许多文献把ITAE 性能指标作为单输入单输出控制系统和自适应控制系统的最佳性能指标[8,9],得到了广泛的应用。另外,从另一思路考虑,一旦选择了某一泛函作为控制系统的性能指标,也就赋予了所设计系统以相应的性能指标。如:二次型积分泛函最小适用于以能耗最小为性能指标的控制系统;误差绝对值积分最小适用于以燃料消耗最小为性能指标的控制系统;误差绝对值乘以时间积分最小适用于以快速而又平稳为性能指标的控制系统。
利用Matlab 的M 文件编程调试方便和SIMULINK 的可视化、易于构建复杂模型的优点,在SIMULINK 中建立了系统模型和ITAE 指标函数数值生成模块,通过M 文件和SIMULINK模块之间的接口关系,实现了M 文件自动修改控制器参数并调用系统的SIMULINK 模型在该参数下进行仿真计算得到对应的ITAE 指标值。控制系统及ITAE 指标函数数值生成SIMULINK 模块图如图2。
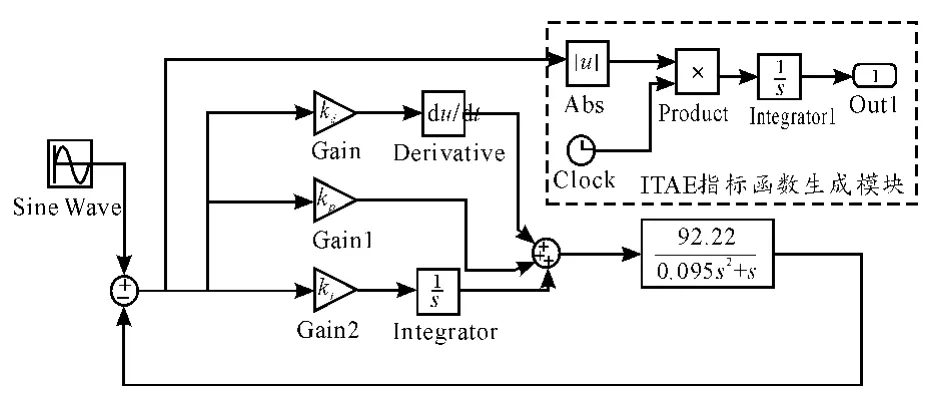
图2 控制系统及ITAE 指标函数数值生成SIMULINK 模块
2.4 算法流程框图
基于遗传算法的PID 控制参数整定流程如图3 所示。

图3 基于遗传算法的PID 控制参数整定流程
3 仿真结果
利用MATLAB 遗传算法工具箱进行仿真,第58 代后进化搜索收敛,得到最优值kp=4.884 9,kd=0.084 36,ki=0.084 36。为检验控制器的控制效果,对控制系统在阶跃和正弦两种典型的输入信号的系统跟踪误差进行了仿真,系统跟踪误差曲线如图4、图5 所示。
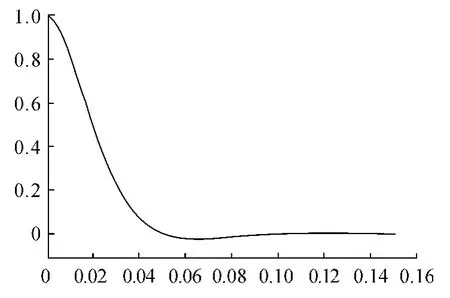
图4 系统对阶跃信号的跟踪误差曲线

图5 系统对正弦信号的跟踪误差曲线
由仿真试验结果可见,随动系统具有较快的响应速度和较小的超调量、控制偏差趋于零。
4 结束语
本文把遗传算法应用到舰炮随动系统PID 控制器参数整定之中。根据遗传算法原理,首先利用广义Hermite-Biehler定理得到PID 控制器参数的稳定域,即保证了系统的稳定性,又确定了算法的优化空间;然后根据舰炮随动系统的控制要求,提出了以ITAE 性能指标为算法的目标函数;最后通过仿真验证了方法的有效性和可行性。本方法可为工程设计人员提供工程指导,具有一定的工程应用价值。
[1]任挺,焦自平,徐文科.舰炮随动系统满意PID 控制器设计[J].火炮发射与控制学报,2009(4):55-57,65.
[2]HOLLAND J H.Adaptation in natural and artificial systems[M]. Michigan: Ann Arbor University of Michigan Press,1975.
[3]GOLDBERG D E. Algorithms in Search,Optimization and Machine Learning[M].New York:Addison-Weley,1989.
[4]徐文科,焦自平,余勃彪.模糊控制器在舰炮随动系统中的应用[J].舰船电子工程,2010(8): 186-188,198.
[5]MING-TZU HO,ANIRUDDHA DATTA,S P BHATTACHARYYA.Generalizations of the Hermite-Biehler theorem[J].Linear Algebra and its Application,1999:135-153.
[6]MING-TZU HO,ANIRUDDHA DATTA,S P BHATTACHARYYA. Generalizations of the Hermite-Biehler theorem:the complex case[J].Linear Algebra and its Applications,2000:23-36.
[7]项国波. ITAE 最佳控制[M]. 北京: 机械工业出版社,1986.
[8]徐峰,李东海,薛亚丽.基于ITAE 指标的PID 参数整定方法比较研究[J].中国电机工程学报,2003,23(8):206-210.
[9]朱红萍,罗隆福.基于ITAE 指标的PID 控制器参数优化设计[J].电气自动化,2009,31(6):37-39.
[10]程远斌. 某型舰炮的失控与改进[J]. 四川兵工学报,2011(7):7-9.
[11]吴宇航,崔敏.摩擦力矩对舰炮随动系统低速平稳性的影响[J].火力与指挥控制,2011(7):85-87.
[12]李克玉,田福庆,杜海东.某型舰炮随动系统的机电耦合建模及仿真[J].四川兵工学报,2011(4):9-13.
[13]邵中年,张志瑞. 基于根轨迹法的随动系统PID 控制[J].四川兵工学报,2012(2):94-96.

