遗传算法优化的整车7自由度EPS控制仿真

张立军，江汇洋

Zhang Lijun, Jiang Huiyang

（辽宁工业大学 汽车与交通工程学院，辽宁 锦州 121001）

0 引 言

EPS是新一代智能转向系统的基础， EPS系统不仅要求能够满足基本的转向轻便性，而且要求提高高速行驶时的操纵稳定性。国内对EPS的建模往往都只针对转向系统进行分析，较少考虑整车、轮胎等与转向系统之间的相互影响。因此文中建立了7自由度车辆平面运动模型，除了车辆纵向、侧向和绕z轴的横摆自由度，还包括4个车轮绕其轴线的转动自由度，在应用现代控制理论基础上进行整车仿真研究。

1 EPS 数学模型建立

EPS系统可划分为转向柱、输出轴、齿条 3个部分。因为轮胎与地面产生摩擦力，转向时产生回正力矩，所以模型引入转向阻力[1]。

转向盘与齿轮齿条模型

电动机模型

Je、Jh、Jm和 Be、Bh、Bm分别为转向轴、转向盘和电动机的转动惯量和阻尼系数，θe、θh为转向盘与输出轴的输入转角，Td、Tm为作用在转向盘的转向转矩和电动机的电磁转矩，Ksen为转矩传感器刚度，mr、br为转向机构及齿条的等效质量和等效阻尼系数，xr为齿条位移，Fr为转向阻力，im为减速器减速比，rp为小齿轮半径。

2 整车系统数学模型建立

2.1 轮胎模型建立

汽车在行驶过程中轮胎对整车动力学有着很大的影响作用。需要建立能够反映轮胎复杂力学特性的轮胎模型[2]。其中魔术轮胎模型有较高精确度和广泛的适用性。

魔术公式的一般表达式为

在纯滑移工况下，纵向力以垂直载荷和滑移率为输入；侧向力以垂直载荷和侧偏角为输入；回正力矩以垂直载荷和侧偏角为输入。根据魔术公式的基本结构，在给定参数的基础上，在合理范围内拟定一部分参数（见表1），通过编写s函数得到仿真结果。

图1～图3所示为利用魔术轮胎公式计算得到的在纯滑移工况下的力学特性。可见，魔术公式较好地反映了轮胎纵向力、侧向力和侧偏角、滑移率之间的耦合关系。

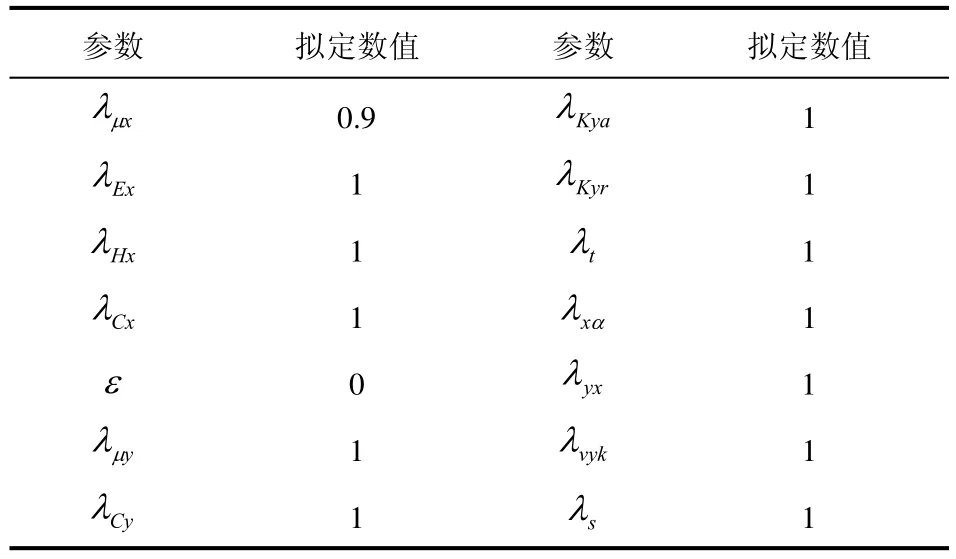
表1 魔术公式拟定参数

2.2 纵向附着系数评估的双指数模型

在车辆系统动力学中双线性简化模型得到一定应用，模型简单，计算量小，但精度较差。非线性拟合的带指数多项式的道路附着系数模型μ=A-BS-Aexp(-as)在滑移率较大时线性化明显，存在偏差[3]。

综合前人的研究成果，文中使用双指数道路附着系数模型。

表2 常见路面特征因子

各种工况及行驶条件下，路面附着特征参数公式为

双指数项的地面——轮胎力学模型为

其中：

对a进行迭代

双指数项的地面——轮胎力学模型，不但能够随时掌握路面附着系数的变化，而且引入路面因子，提高了模型的通用性。通过计算得到轮胎滑移率并输入到魔术轮胎s函数模块中，如图4所示。

2.3 整车模型建立

文中建立了 7自由度动力学方程，侧倾转向效应较能准确地反映实际情况。

纵向动力学方程

侧向动力学方程

横摆动力学方程

4个车轮的动力学方程

Iwi为车轮的转动惯量，M(t)为制动力矩，Fi是车辆受到的外力。

车辆运动过程中的轮胎侧偏角公式

受侧倾影响，轮胎垂直载荷的数学模型为

将轮胎垂直载荷与侧偏角输入到魔术轮胎模型，可求出侧向力与回正力矩。

第i个车轮的转动角速度为ωi，则滑移率将车轮动力学方程和双指数附着系数方程联合如图5所示，可求得滑移率，将滑移率输入到魔术轮胎模型可得纵向力。将整车模型与轮胎模型连接，将回正力矩作为转向阻力输入到转向模型，转向盘转角通过传动比得到前轮转角，计算轮胎侧偏角，可以得到 EPS 的整体仿真模型，在经过EPS系统、轮胎模型及整车之间的计算关系后，可得出横摆角速度等操纵特性的仿真结果。

3 EPS系统控制策略仿真

3.1 PID控制

PID控制器是在自动控制中经常使用的模块，应用 PID电压控制法，将工程应用中标准的数学模型加入到转向系统中，得

调节参数Kp，Td，N得到控制电压，根据电压平衡方程计算助力电流，求得电磁转矩输入到转向系统电动机模型。

3.2 基于遗传算法优化的BP神经网络控制

助力特性电流是指转向盘转矩与电机电磁转矩的映射关系，通过有限的数据得到这一复杂的解析式会造成一定的盲区，应用BP神经网络对助力特性电流离散样点的训练拟合，可以获得更为合理的助力特性曲线。

BP神经网络虽然获得了非常广泛的应用。但是也存在一些缺陷，例如：学习收敛速度太慢，不能保证收敛到全局最小点；另外，网络结构、初始连接权值和阈值的选择对网络训练的影响很大，但是又无法准确获得，针对这些特点可以采用遗传算法对神经网络进行优化。

遗传算法优化 BP网络的基本原理是用遗传算法来优化 BP网络的初始权值和阈值，使优化后的 BP网络能够更好地预测系统输出。遗传算法优化 BP网络主要包括种群初始化、适应度函数、交叉算子、选择算子和变异算子等[4,5]。

根据测试样本表2，以转矩和车速为输入，以助力电流为输出，构建BP网络。遗传算法的基本参数为个体采用浮点数编码法，种群规模是30，总进化次数是80次。BP算法中err_goal=0.002，lr=0.01。

表3 不同车速下的K(V) [6]

根据表3的计算结果，采用多项式拟合

根据助力电流特性公式

Matlab部分主程序：

%进行遗传算法：

%遗传算法求解最佳阈值、权值：

%优化过的阈值、权值赋给BP网络：

计算神经网络的误差平方和，若达到预定值2，则以遗传算法的优化初值作为初始权值，用BP算法训练网络，直到指定精度，如图6所示。

最后得到遗传算法优化过程中最优个体适应度值变化，适应度高的个体被保留下来，组成新的群体，新群体中各个体适应度不断提高，直至满足最佳适应度，如图7所示。

用优化过的 BP神经网络拟合输出的助力电流值误差极小，通过助力电流求得电磁转矩输入到转向系统电动机的模型。

3.3 整车系统仿真结果

利用Matlab/Simulink建立EPS系统模型并对整车操纵稳定性进行仿真研究。通过Matlab程序生成BP神经网络Simulink模块，将转向盘转矩和车速输入到优化好的权值、阈值模块，输出BP网络拟合好的特性电流值到电动机，电动机输出助力转矩。同时调节PID控制参数Kp、Kd，输出电压，通过计算得到的电流值到电动机，输出助力转矩与神经网络控制进行对比，如图 8所示。文中取值Kp=9.5、Td=10、N=10。

分别采用两种不同的控制策略对横摆角速度、转向盘转矩和转向盘转角进行仿真。采用优化过的神经网络控制方法后，超调量明显减小，稳定时间缩短，提高了汽车操纵稳定性，如图9～图11所示。

4 结 论

在简化模型基础上对汽车电动助力转向系统和整车模型进行联合仿真，兼顾汽车行驶时的操纵感和汽车稳定性，结果表明，所建立的模型可以较好地反映汽车转向时的动态特性，所采用的控制策略取得了良好的控制效果。

[1]余志生. 汽车理论[M]. 北京：机械工业出版社，2005.

[2]郭孔辉. 汽车操纵动力学[M]. 长春：吉林科学技术出版社，1991.

[3]边明远. 汽车防滑控制系统道路识别技术及车身速度算法研究 [D]. 北京理工大学，2003.

[4]陈海军. 基于遗传优化的神经网络控制策略的研究 [D]. 燕山大学，2010.

[5]ToshinariShiotsuka，AkioNagamatsu. Active control of drive motion of four wheel steering car with neural network. SAE paper，940229.

[6]施国标，申荣卫，林逸. 电动助力转向系统的建模与仿真技术[J]. 吉林大学学报（工学版）2007，37（1）：31-36.