平面交线求法及可见性判断

郑作龙

[摘要]空间两平面的相交问题，是画法几何的重要内容之一，平面交线求法具有一定的技巧性，本文就有形平面的交线求法及可见性判断作个探讨。

[关键词]有形平面；交线求法；可见性判断

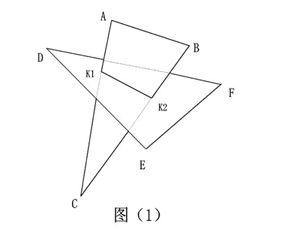
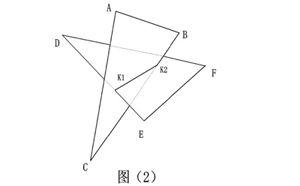
有形平面往往表现为几何多边形，相交两平面间的关系可分为两种类型：其一，某平面的两条对应边线分别穿过另一平面（全贯），如图（1）中△ABC的AC和BC边穿过△DEF。其二，相交两平面中各有一条边线分别穿过对方平面（互贯），如图（2）中△ABC的BC边穿过△DEF，同时，△ABC亦被DE边所穿过。这里的Km₁和Km₂为对应边线与另一平面的“贯穿点”，其连线即两平面间的交线。

空间两平面的交线求法可运用辅助平面法（即三面共点的原理）来求解。具体到有形平面求交时，一般做法是包含平面的边线作辅助平面，求出两个贯穿点然后连线。如图（3）求△ABC和△DEF的交线，可分别包含AC和EF边作辅助正垂面，求出对应的贯穿点Km₁和Km₂，将两个贯穿点连接起来，就是两个平面的对应交线。

值得注意的是，仅根据图（3）已知条件，无法判断线面间的贯穿关系。解题时，究竟应该包含哪条边线去作辅助平面不得而知，也就难以准确地求出两个对应交点。其实在求作两平面的交线问题上，只要善于分析，弄清相交两平面对应边线与另一平面交点之间的内在联系和投影规律，问题也就变得简单了。

参与相交的两平面之边线，只要不与另一平面保持平行，就一定能找到对应交点。虽然有时所作辅助平面求出的不一定是真正意义上的交点Km₁和Km₂，但它一定在所求交线Km₁ Km₂的延长线上。如图（3）中的km₂就是边线DF和△ABC平面轮廓外的对应交点，它必在交线Km₁Km₂的延长线上。求解过程中倘若首先求出的是Km₁和Km₃点，其连线必交于AC边上的Km₂，连接Km₁ Km₂同样能求出交线。这里Km₂km₃不在两平面投影轮廓的公共范围内，不属于交线的投影。因此，两平面相交时，平面上任一边线与另一平面的关系不平行则相交，只要相交就能求出对应交点，且交点一定在两面交线（或其延长线）上。

由此可见，在相交两平面的投影图中，无论包含哪条边线作辅助平面均能求出对应交点（当边线平行于另一平面时例外），且交点属于两平面交线。作图时任取两条边线作辅助平面就能求出平面交线。

应注意的是，作图的关键在于求出“贯穿点”，求解的时候可能出现两种种情形：

1.所求交点同时位于两平面的轮廓范围内（如图3中的Km₁和km₂），此点即贯穿点，可直接定出交线。

2.所求交点位于某个平面的轮廓线上（如图3中的km₃），此时应通过该点连线，找到连线上的对应贯穿点，最后确定交线。

关于可见性的判断：空间两平面相交时，其轮廓线在投影图中不可避免地存在遮挡关系。当求出平面交线后，还应进一步判断出对应轮廓的可见性，以确定交线周围重叠部分轮廓的虚、实关系。

在图（3）所示的正面投影中，当交线Km₁Km₂求出后，需要判断Km₁1、12、……56、6Km₁各段投影的可见性，然后用规定的线型完成全图。方法是任取一对重影点，判断出其相邻两条边线的可见性，并由此推出其余各段边线的可见性。这里以重影点1（m）为例来说明可见性的判断方法：点1属于边线EF、点M属于边线BC，由于1m_Y大于Mm_Y，故判断出Km₁1段为实线、12段为虚线，其余各段则依次为实线、虚线的交替变换，不需另取重影点来作判断。也就是说在平面的投影中，重叠轮廓部分相邻两段图线的性质必定相反，表现为实线和虚线相间，判断一对便知全部。要注意的是，这里所指的“重影点”，一点是两个平面轮廓上的对应点。另外，水平投影的可见性判断方法相同，恕不赘述！

参考文献

1、西安交通大学工程制图教研室《画法几何及工程制图》.陕西科学技术出版社.1982

2、周鹏翔刘振魁主编《工程制图》高等教育出版社2006