交交变频系统环流最小控制策略
李鹏飞,严欣平
(重庆科技学院,重庆 401331)
1 引言
交交变频是指由交流变交流的频率变换器,由于采用晶闸管半控型器件和无直流环节,变换器转换效率高,可方便地实现四象限运行,节能效果明显,在大功率、低转速交流调速场所被广泛应用。
交-交变频器供电系统是一个十分复杂的非线性系统,采用三相桥式电路组成的三相交交变频器所有晶闸管器件多,接线复杂,控制技术含量高,尤其是有环流工作方式交交变频电路,环流的存在与分析是实现三相交交变频器可靠工作的关键,本文重点研究了如何控制交交变频电路中 的环流大小,如何对调节过程中的动态环流进行 限制,同时对影响交交变频器运行的诸多因素进行详细的讨论。提出了采用不同的控制和调制信号来获得输出电压函数形式,分析各种影响交交变频系统的环流大小因素,给出了环流最小的控制策略,有效地改善了交交变频环流不利影响,提高了交交变频器工作的稳定性和可靠性。有关谐波问题的研究需要采用开关函数模型。文献[1]均对开关函数模型做了比较详细的介绍,文献[2]对交交变频采用余弦交截法产生确定 触发时刻控制系统进行了环流介绍,但分析比较简略,文献[3]介绍了交交变频器-多相同步 电动机稳态和似稳态等效电路模型的计算方法,相比较而言,本文对交交变频器的环流谐波研究 则更详细、更深入。同时本研究利用控制信号波形来控制回路的环流大小,为无检测可控环流提供研究数据,以适应不同频带负载运行控制要求。
2 交交变频转换特性
三相交交变频电路如图1,而交交变频的每一相输出,其负载电流可以由正组或负组的晶闸管供给,理想情况下变流器应为低阻抗电源供电。当相位控制角恒定或逐渐变化时,输出电流连续,输出电压的平均值为
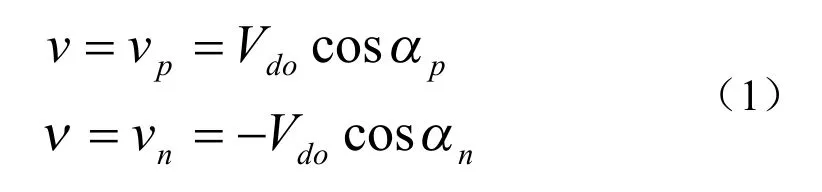
式中:ν为平均输出电压值;Vdo为平均输出电压最大值,α为控制角;n为反组控制角;p为正组控制角。
为满足上述等式,则αn=π-αp,输出电压的平均值在doV+ 和doV- 之间变化,对交交变频器这是相位控制角的控制范围,可以得到变频器在任意极性、任何电压下输出的负载电流。
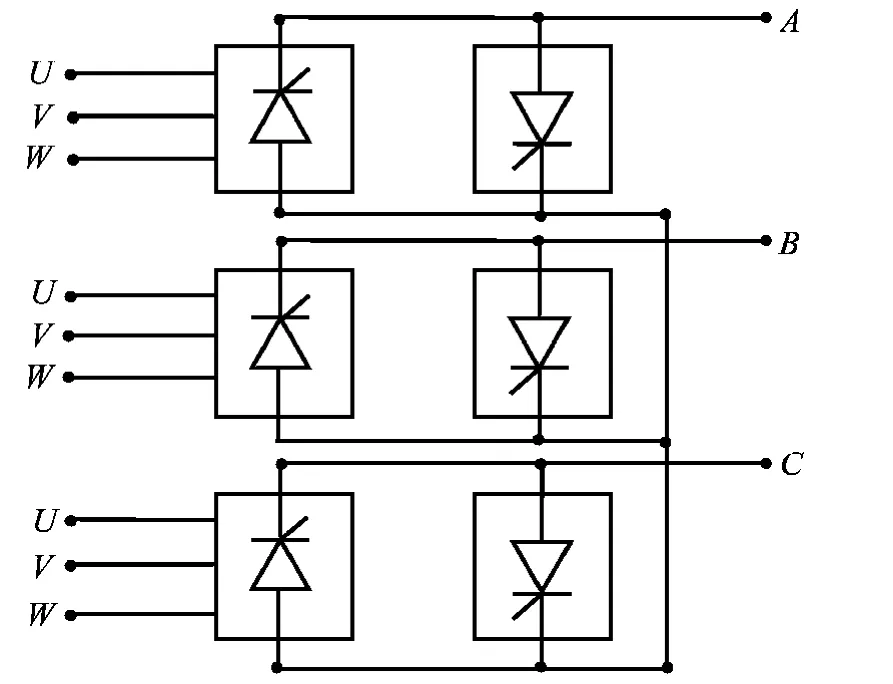
图1 三相交交变频电路 Fig.1 The circuit of three-phase AC-AC frequency converter
由于式(1)中电压瞬时值不相同,必然产生动态环流。假设两组控制角αp和αn周期性地变化,且在0≤α≥π 之间,则α=f(ωct),式中ωc为所需的输出基波频率。若把输出电压v看作是交交变频“动态”输出电压,随时间而变化,那么式(1)的傅立叶级数形式可表示为

则认为是v在给定时间内交交变频电路某组整个导通周期内的平均输出电压,那么输出电压v相当于周期平均输出电压的快速变化,则可忽略不计。
每一组控制角,是由控制电压和电源频率的调制电压比较后决定的,当控制电压变化来改变控制角时,输出电压波形依赖于实际的控制信号与调制信号。
设调制信号分别为余弦和梯形(斜线)信号,取控制信号分别为方波、梯形波、余弦波作为不同的控制方式,可以得到不同的组合控制方式。
组合一:采用余弦调制与余弦控制组合方式推导

因此,cosα=kcosωst
给定α1=k和αv= 0,v≠ 1
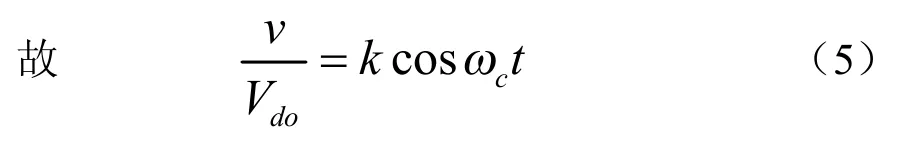
组合二:采用余弦调制与线性控制组合方式推导为


同理可得如表1所示组合控制方式。

表1 控制和调制信号不同组合产生的COSα函数,当0≤Ctω≤π
为方便起见,调制和控制电压均以标么值表示,因此调制函数中,幅值从+1 到-1 之间变化,即当ωst时,为+1,ωst=π 时为-1,ωst=π 时,则为过零线。同样,控制函数由+K到-K之间变化,即+K时,ωst=0,-K时,ωst=π,过零时,ωst=π 从后者来说,K从0 到1 之间变化,提供了一个控制输出电压的方法。
理论证明输出电压为一重复、不连续的时间函数,此函数可以用傅立叶级数来表示,如同上面推导的方法一样能够确定输出的基波和谐波含量的相对幅值控制参数幅值K的函数,其结果列于表2。在表2中交交变频输出电压的波纹频率均忽略不计,并将数据绘制成曲线如图2所示。

表2 交交变频输出电压波形谐波量

图2 输出电压基波幅值α和控制幅值参数k关系曲线 Fig.2 Fundamental wave amplitude of output voltage control of the amplitude parametersαandkcurve
从上4 种组合图分析可知,对控制频率谐波来说:
a)采用方波信号控制方式(组合方式(iii)和(vi)),输出电压谐波分量大,不合适大容量交交变频控制,但线路简单经济。
b)采用余弦控制-余弦调制控制方式(组合方式(i)或(v)),输出电压正弦度好,谐波小,担需要余弦调制信号。
c)采用线性控制-余弦调制控制方式,输出电压增益低,调制比不够。
d)采用余弦控制-线性调制控制方式,输出增益大,但转换特性存在非线性,需要限制最大控制角,防止逆变过程的换流失败。
3 交交变频环流限制
综上所述,交交变频系统在低频输出时,如果正组P 输出电压与负组N 输出电压,同以控制角αp+αn=π 来触发,则两组的平均输出电压相等,但瞬时输出电压并不相等。很显然,P 组和N 组将构成闭环回路产生环流,环流大小由回路阻抗决定。通常采用两种方法限制环流:
a)电抗器环流限制法;
b)分时逻辑控制法,即任何时刻,只允许一组导通,无环流回路,阻断环流的产生。
3.1 电抗器环流限制
如果回路中的阻抗为一感抗X,则环流的瞬时值,可以用环流系数c来表示,
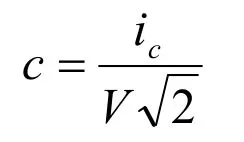
三相半波交交变频电路中,当控制角恒定时,环流平均值的计算如下:
a)控制角在0≤pα≤π/3 范围内
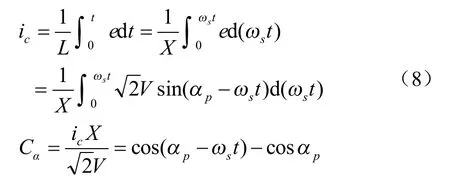
可见最大电流为0.5,发生在α=π/3 时。
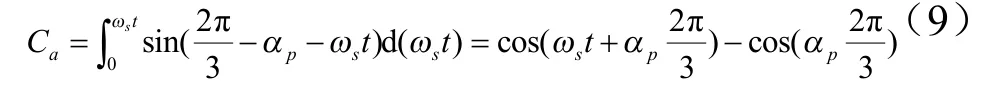
下面有两种情况

根据环流的对称性,环流系数与0≤pα≤π/2相同,这里不再赘述。
交交变频电路中控制角是连续变化的,如果要得到整个控制周期的平均环流参数mC则:
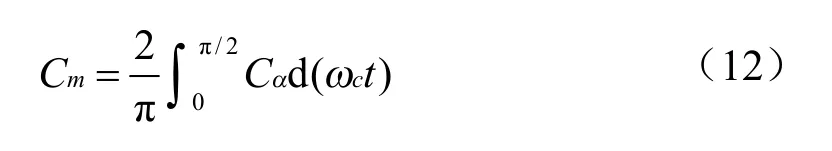
式中:Ca为随控制角而变的时间函数,其大小取决于变频器的传递特性。
图3是环流系数Cm随控制参数幅值k变化曲线图。由图3可知,在不同控制信号作用下,环流的大小是各不相同的,但总体变化不大。设负载电流为Ⅰ,并为正弦,则在正组与负组之间的平均负载电流为,表明该值比环流平均值略大,其近似条件是:

那么在上述电抗情况下,环流峰值可接近满载电流峰值两倍。这在交交变频相同控制设计时必须加以认真考虑。
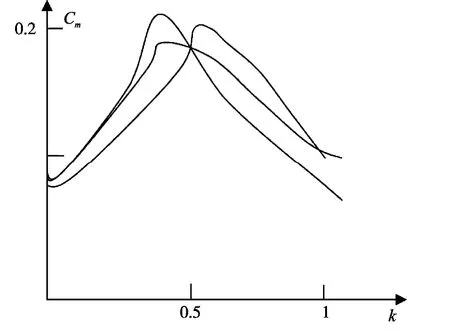
图3 控制幅值k与环流系数Cm的变化曲线 Fig.3 Amplitude control loop coefficientskandCmcurves
3.2 组间环流限制电抗器
在交交变频电压输出的正组与负组之间,由于存在环流电压必须接入大电感,将环流限制在允许工作范围内。但电抗器容易出现直流磁化现象,故必须使负载电流电感仅为环流电感1/4 左右,才能确保交交变频电路的正常工作。按照ap+an=π 工作制进行相位控制,理论上不产生环流,但实际工作时很难做到无环流,因控制角随时间变化,有可能产生“瞬时环流”。经实验发现对线性调制和余弦控制交交变频电路,表明环流随频率增高而增大,即近似与频率和幅值成正比。
4 实验结果与分析
为验证有环流工作方式交交变频电路中,控制环流的大小与分析,本文进行了Matlab/simulink仿真,图4分别是交交变频器所采用的梯形波、三角波、余弦波调制信号,图5是三种调制信号产生的输出电压Ud、输入电压Ur、输出电流Ⅰd仿真波形,图6是三种调制信号生产的交交变频器的负载电流和环流,从负载结果图可以看出,余弦波调制的输出电压波形正弦度好,环流动态响应快,环流小;其次是三角波调制输出电压电压波形正弦度较差,环流较大;而梯形波调制输出电压波形正弦度差,环流大。采用80C196MC 微机控制控制系统原理如图7,交交变频控制系统输出容量2.2 kW,电压380 V,频率可从5 Hz 到100 Hz 调节,异步电动机,Pe=1 kW,Ue=380 V,ne=1 455 r/min,w1=108匝,Δ 接法,r1=1.375 Ω,X1e=2.43 Ω,r2'=1.047 Ω(折算值),X2'=4.4 Ω(折算值),GD2=1.19(N·m2)进行空载运行试验结果(ML=0)。

图4 梯形波、三角波,余弦波调制信号 Fig.4 Trapezoidal,triangle and cosine wave modulation signal
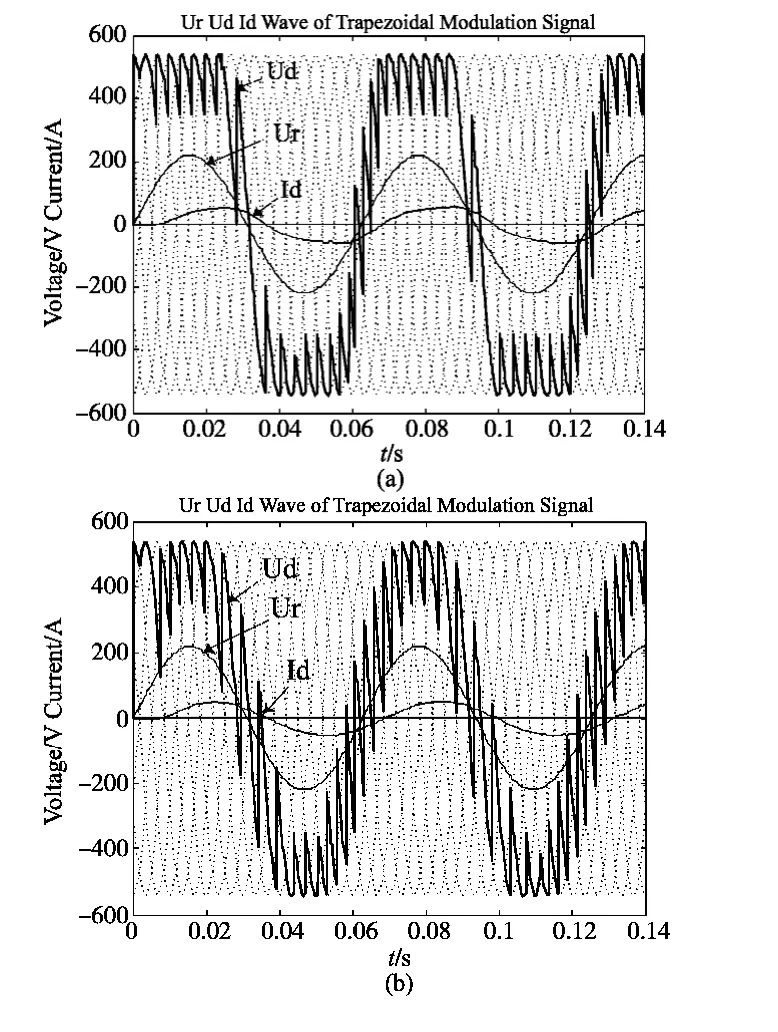

图5 梯形波、三角波,余弦波调制信号产生的仿真结果 Fig.5 Simulation results of the trapezoidal,triangle and cosine wave modulation signal
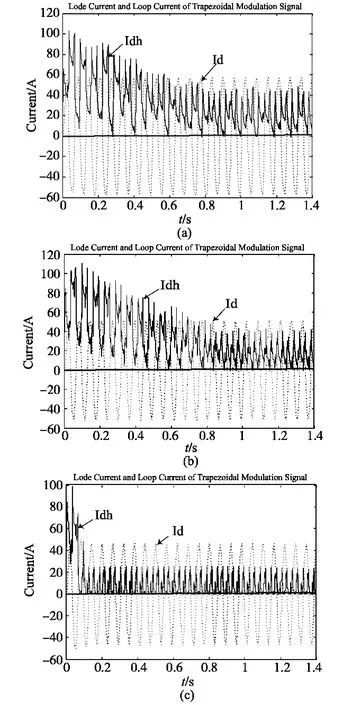
图6 梯形波、三角波,余弦波调制信号产生仿真结果 Fig.6 Simulation results of the trapezoidal,triangle and cosine wave modulation signal
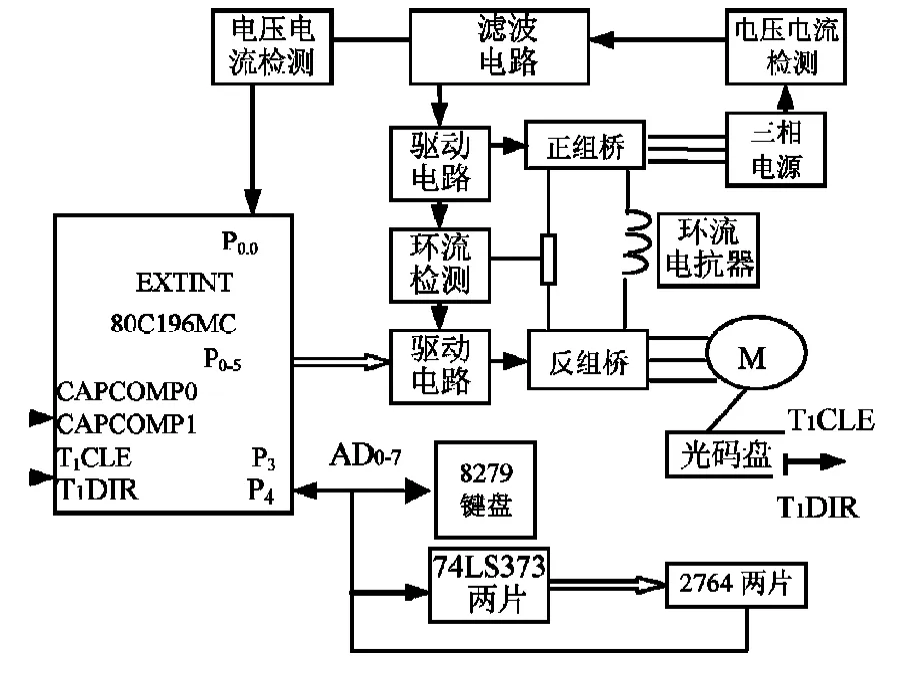
图7 交交变频控制系统框图 Fig.7 A control block diagram of AC-AC frequency converter
环流大小随着控制的幅值而变的实验曲线如图8。曲线①是iv 控制组合理论计算曲线,曲线②是时实测值曲线,曲线③是ω= 1时测试曲线。从图中可见,当时,实测验值与计算值相近,但当ω=1时,只有在k≤0.4 时,才互相一致。实验中发现,角的整定值变化1°,就会引起环流系数从0.08 增为0.18。
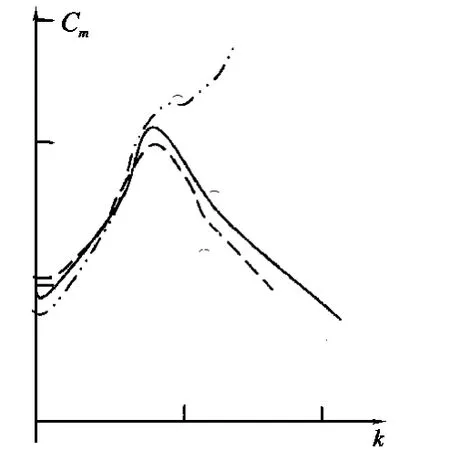
图8 变化的计算值与实测值关系曲线 Fig.8 Relationship curve between calculated and changed measured values
5 结论
通过仿真验证与实验测试,本文对交交输出电压与控制频率的谐波含量进行了详细的研究,证明了本分析方法的正确性,对交交变频电路环流的大小,从控制方面进行了深入讨论。就谐波含量而言,在大容量交交变频控制系统中,采用余弦控制信号较为理想;对小容量交交变频控制系统,采用三角控制信号可得到近似正弦波输出,其控制线路简单,但谐波含量较大,环流突出,设计应用时必须认真加以考虑。
[1] 许勇,许镇琳,蔡昆,等.数字式交-交变频器的仿真模型和分析[J].电力电子技术,2002,34(1):49-51.
[2] 黄亮,任永峰,贺刚,等.有环流交交变频传动系统的无功功率的研究[J].电力科学与工程,2003(2):13-16.
[3] 林桦,邹云屏,王兴伟.交交变频器-多相同步电动机稳态和似稳态等效电路模型[J].电工技术学报,2005,20(4):15-20.
[4] 马小亮.大功率交-交变频调速及矢量控制技术[M].北京:机械工业出版社,2004.
[5] 潘庭龙,姜建国.交交变频矢量控制系统的CPLD 数字触发电路[J].电力电子技术,2003,37(6):74-75.
[6] 逯志宏,刘广友,马文静.大功率交交变频全数字矢量控制系统在济钢中厚板精轧机上的应用[J].冶金自动化,2004,28(2):48-49.
[7] 万军,孙昌印,孟君.大型H 型钢生产线轧机主传动系统选型[J].电气传动 ,2008,38(4):17-19.

