高墩桥梁的P-Δ效应及简化计算方法

崔 猛

（兰州交通大学土木工程学院，甘肃兰州 730070）

0 引言

桥墩在水平地震力作用下产生水平变位，使作用在墩顶上的上部结构的重力荷载以及墩身自身的重力荷载产生了偏心，在桥墩内将引起二次内力和变形（称P-Δ效应）。在线性体系中，P-Δ效应也会产生非线性影响[1]。

P-Δ效应是各种桥墩中存在的一般性力学现象，也是较精确地震反应分析中必然要考虑的普遍性问题。我国现行铁路工程抗震设计规范（2009）在此方面没有规定。美国加州规范[2]规定：“设计中应考虑重力荷载对水平位移的动力效应，墩中产生塑性铰后考虑P-Δ效应的墩顶位移值只能通过非线性时程反应分析精确计算。有些条件下P-Δ效应可以忽略不计”。我国公路桥梁抗震设计细则[3]规定“墩柱的计算长度与矩形截面短边尺寸之比大于8，或墩柱的计算长度与圆形截面直径之比大于6时，应考虑P-Δ效应”。我国台湾规范[4]规定“采用稳定指数Qs来描述P-Δ效应的影响，当Qs＞0.05时，须考虑P-Δ效应的影响。大震下墩柱的位移会很大，P-Δ效应可能会造成动态不稳定，当Qs＞0.25时，宜进行非线性时程反应分析，计算结构的抗震能力”。尽管目前许多桥梁抗震规范都要求地震反应分析时应考虑P-Δ效应的影响[2-4]，但考虑方法不统一。不同学者的P-效应研究结论也不尽相同[5-6]。目前，关于P-Δ效应对结构动力反应影响的主要观点是，P-Δ效应往往增大地震反应，弹性小变形下影响较小。

本文定量研究P-Δ效应对铁路高墩桥梁地震反应的影响及其简化计算方法。

1 考虑P-Δ效应的地震反应分析方法

不考虑P-Δ效应影响时，在水平地震作用下结构体系的运动方程为：

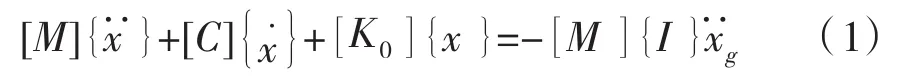
当考虑P-Δ效应影响时，结构体系的运动方程为:

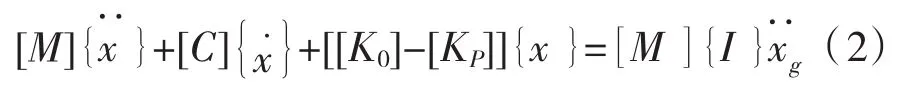
本文采用直接形成等效侧向力的方式建立桥墩的影响刚度矩阵[KP][7]，作用在各质点上的等效侧力自上而下逐个计算（各质点编号也自下而上编排，见图 1）。图 1（c）中 Wi（i=1,2,3…，n）是第 i个质点所受的重力荷载，为i单元以上的重力荷载之和。xi是第i个质点相对于墩底的水平位移，Δi是相邻质点间的相对位移，且有以下关系Δi=xi-xi-1。第i个质点处的受力和变形情况见图1（d），图中Qi是i质点处的剪力。

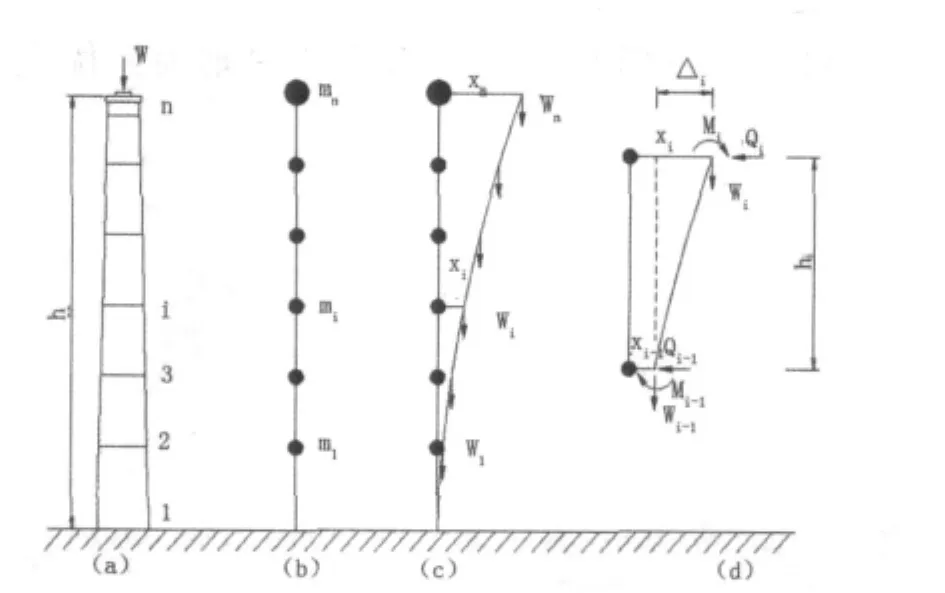
图1 影响刚度矩阵计算图示

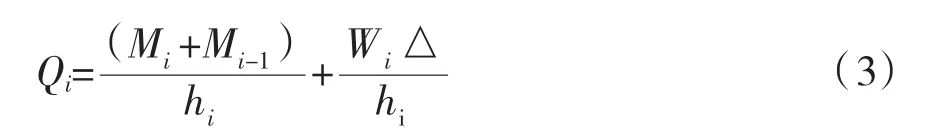
第i节点由重力效应作用的等效附加剪力为：

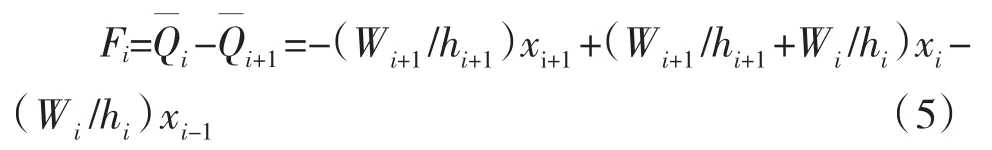
桥墩的等效侧向力向量{F}可以写成:

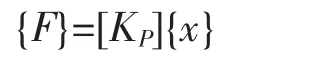
式中，{F}为体系的等效侧力向量;[KP]为体系的影响刚度矩阵。

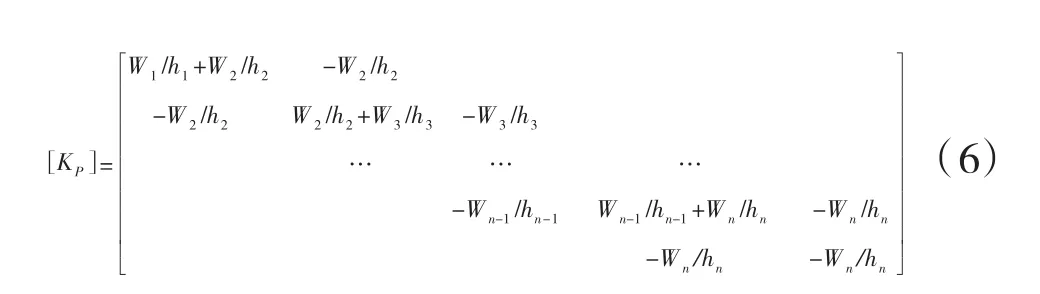
2 计算实例

为了研究P-Δ效应对高墩地震反应的影响，选取某铁路桥梁的4号高墩为研究对象（见图2）。4号墩身高H=92 m，墩帽高3 m。桥墩为顺、横桥向及截面内外均有放坡的空心矩阵截面。单跨简支钢桁梁重7 600 kN（含二期恒）。桥址的设计水平地震基本加速度A=0.2 g，II类场地，特征周期为0.55 s。

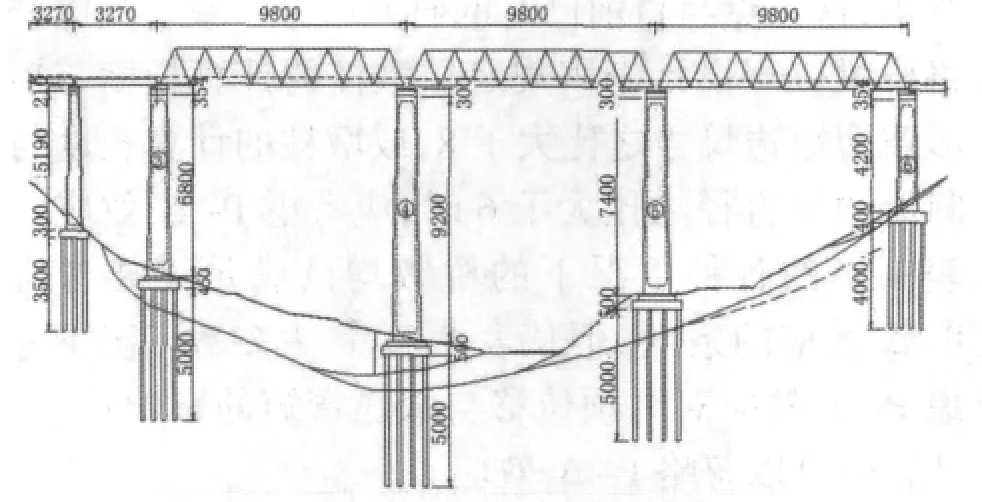
图2 铁路高墩桥梁立面图（单位：cm）

顺桥向输入图3所示的水平反应谱曲线,考虑高阶振型的影响进行弹性地震反应分析。保持输入地震动不变，以墩顶水平位移与墩底弯矩为指标，通过分别调整梁重与墩高H考查P-Δ效应的变化规律。计算中按墩底与地面固定考虑，分析结果列于表1。

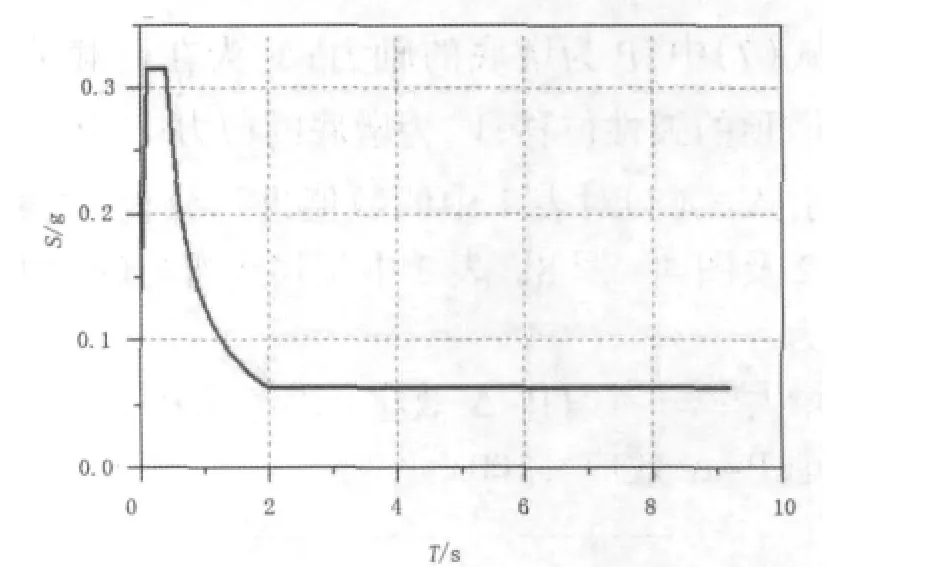
图3 反应谱曲线

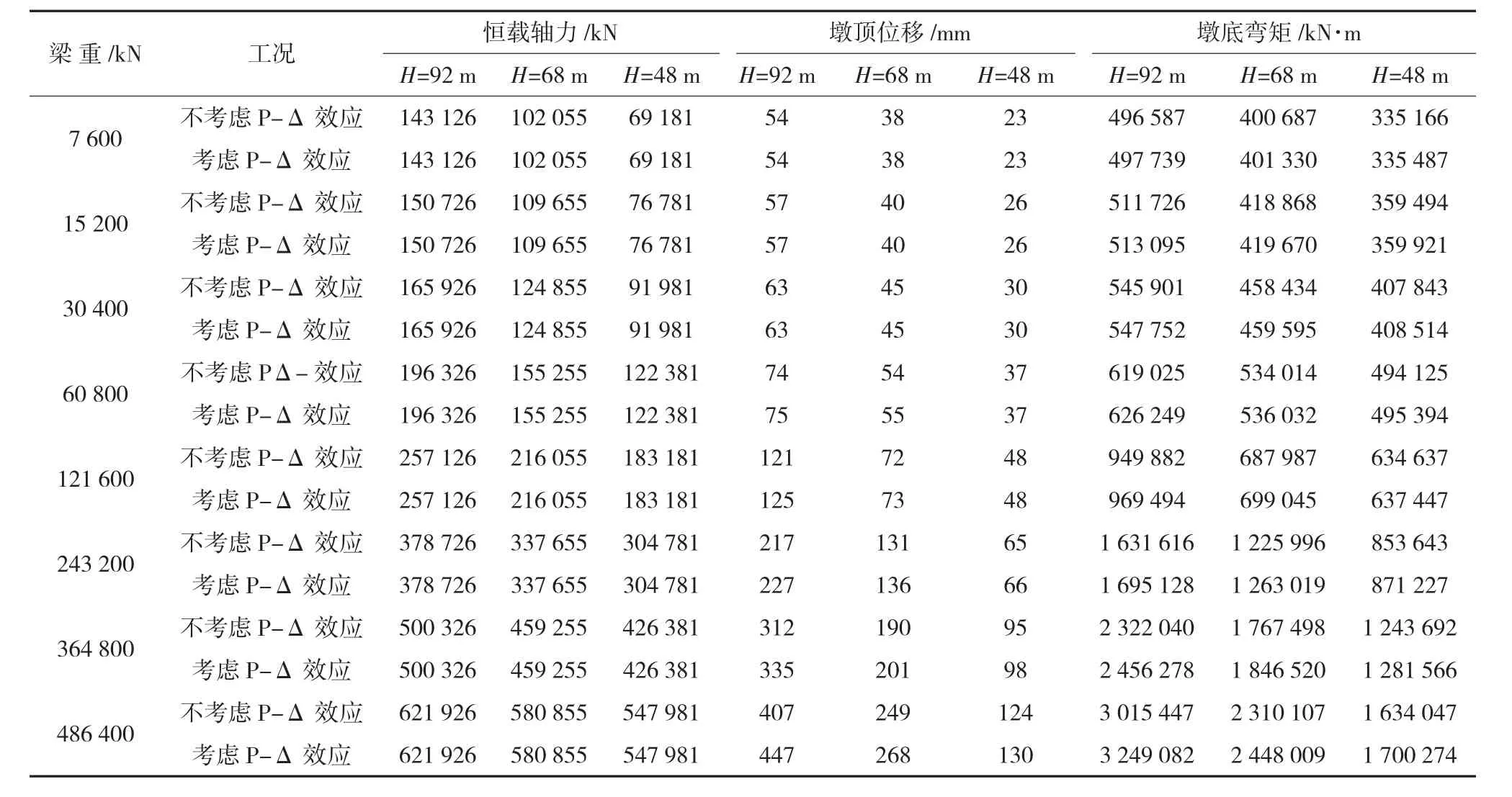
表1 P-Δ效应对高墩地震反应的影响

由表1可以看出，对于各种墩高及梁重而P-Δ效应都会放大地震作用下的墩顶位移与墩底弯矩，这一点与目前已有的研究结论一致。我国公路桥梁抗震设计细则规定“墩柱的计算长度与矩形截面短边尺寸之比大于8，或墩柱的计算长度与圆形截面直径之比大于6时，应考虑P-Δ效应”。表1中的各种工况下的桥墩均已满足需要考虑P-Δ效应的条件。但从表1来看，大多数工况下考虑P-Δ效应对墩顶位移与墩底弯矩的影响较小，计算中可以忽略P-Δ效应。

因此，考虑P-Δ效应对铁路高墩桥梁的影响判别条件尚须探讨。

3 P-Δ效应的判别条件与简化计算方法

台湾桥梁抗震规范[4]中的稳定指数Qs的表达式，如下：

式（7）中，P 为墩底的轴力；Δ0为在荷载 Vu作用下墩顶的弹性位移；Vu为墩底的剪力；lc为墩高。

引入式（7）对表1中的数值进行分析，结果列于表2及图4～图8。表2中位移或弯矩的增大率定义为：

增大率=（考虑P-Δ效应-不考虑P-Δ效应）/不考虑P-Δ效应×100。

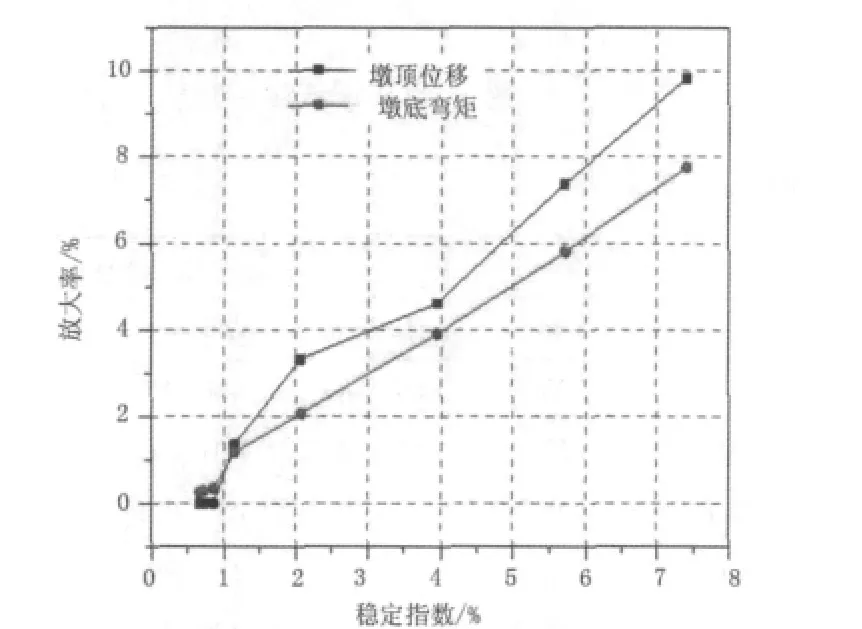
图4 92 m高墩的P-Δ效应增大率

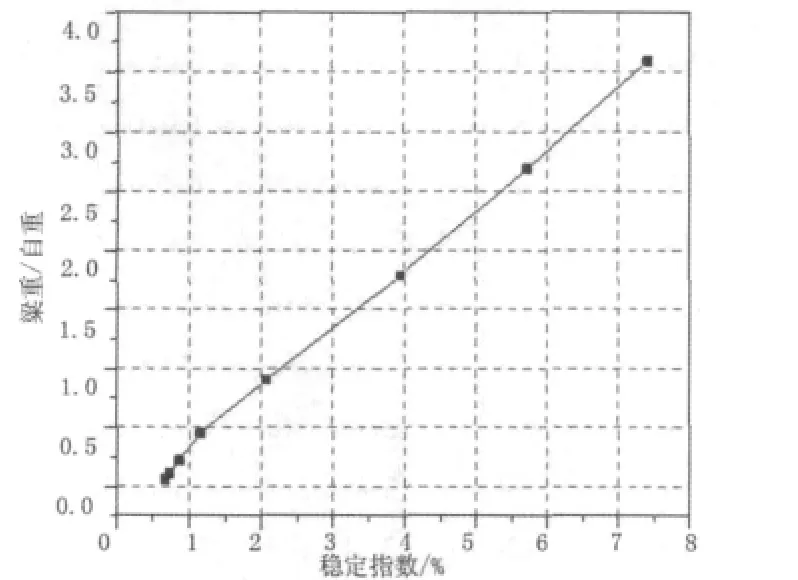
图5 92 m高墩的梁重/自重关系图

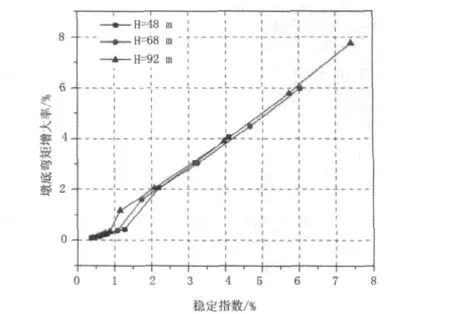
图6 稳定指数与墩底弯矩增大率

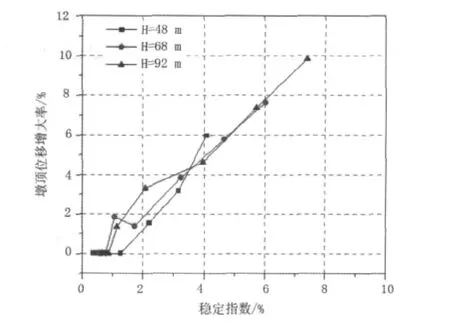
图7 稳定指数与墩顶位移增大率

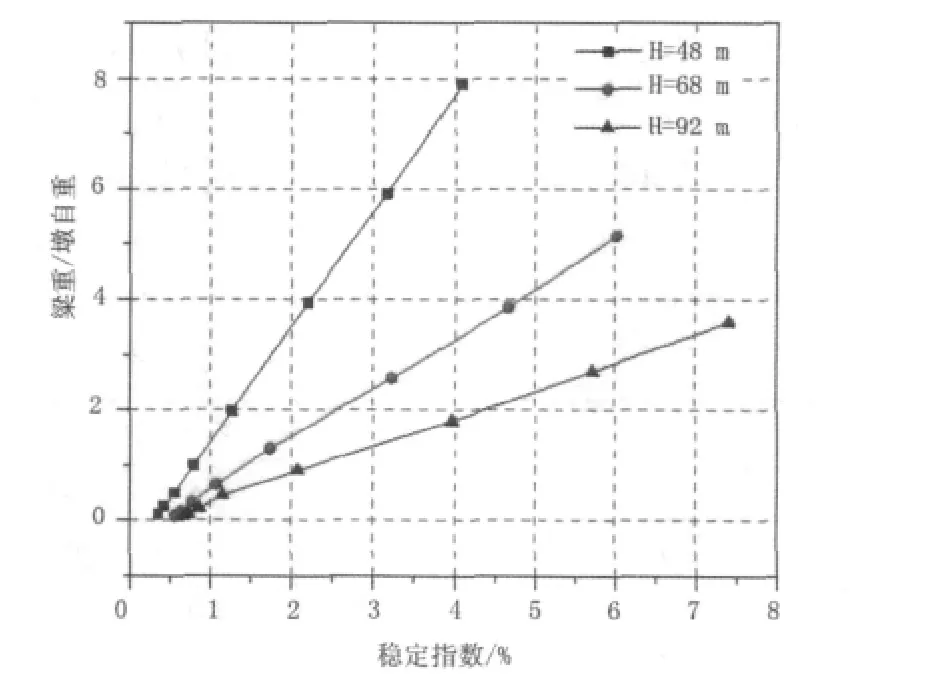
图8 稳定指数与梁重及自重之比

从表2及图4～图8可以看出，墩高保持不变时，P-Δ效应对墩顶水平位移和墩底弯矩的影响与梁重或墩梁重之比及稳定指数有关，并且各墩高的条件下均有此规律。稳定指数与墩梁重之比线性相关，在0～8%范围内，地震作用下墩顶位移及墩底弯矩的P-Δ效应的增大率可以用稳定指数近似表示。多遇地震下铁路高墩桥梁抗震设计时，可以采用稳定指数Qs来判定P-Δ效应的影响。P-Δ效应对墩顶位移与墩底弯矩的增大值可近似等于稳定指数Qs。当稳定指数Qs＞5%时，P-Δ效应对高墩地震反应的影响也约为5%，因此须考虑P-Δ效应的影响。基于以上研究，本文给出的P-Δ效应简化计算公式如下：

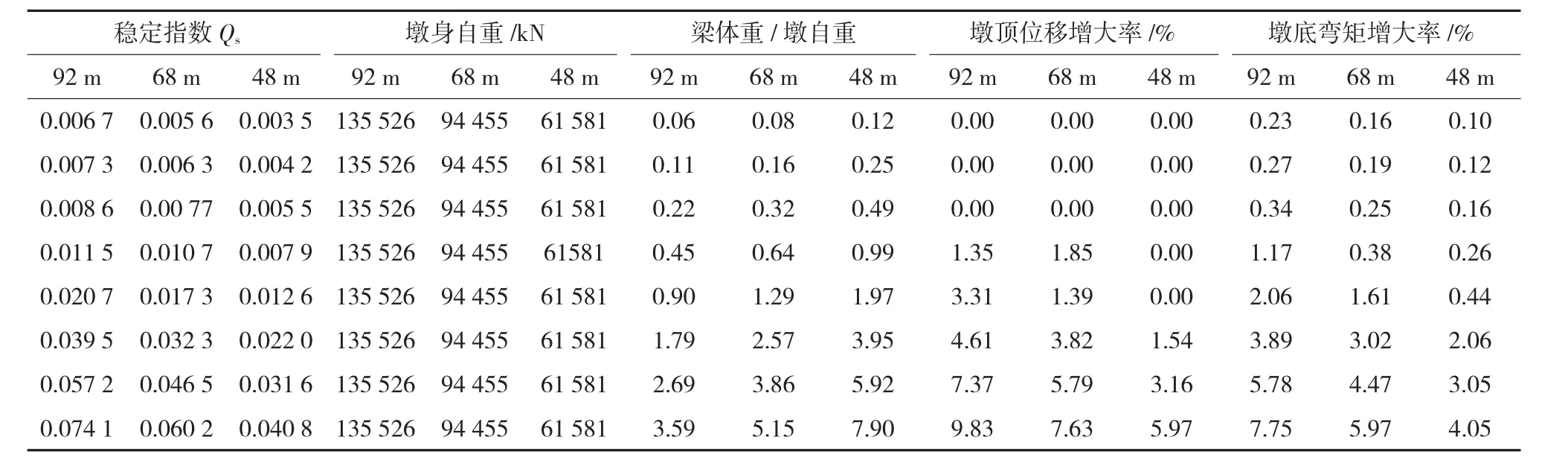
表2 稳定指数的影响因素

式（8）、（9）中 Mdelta、Δdelta分别为考虑 P-Δ 效应的墩底弯矩、墩顶位移；M、Δ分别为不考虑P-Δ效应的墩底弯矩、墩顶位移；Qs为稳定指数，按式（7）计算。

4 结论

（1）P-Δ效应会增大高墩的墩顶水平位移与墩底弯矩，不考虑P-Δ效应偏于不安全。

（2）墩高不变时，稳定指数随梁重与墩重之比增大而增大。

（3）梁重与墩重之比不变时，稳定指数随墩高增大而增大。

（4）P-Δ效应对墩顶水平位移与墩底弯矩的增大率与稳定指数有一定的相关性。

（5）P-Δ效应对高墩墩顶水平位移与墩底弯矩的放大可近似用稳定指数表示。

[1]胡聿贤.地震工程学[M].北京：地震出版社，2006.

[2]Caltrans seismic design criteria version 1.4[S],2006.

[3]中华人民共和国交通运输部.公路桥梁抗震设计细则[S].北京：人民交通出版社，2008.

[4]台湾交通部.铁路桥梁耐震设计规范[S].台北：金新印刷影印行，2006.

[5]李睿,董明.考虑P-Δ效应的高墩抗震计算[J].云南工业大学学报,1999,15（1）:61-66.

[6]刘坤,陈兴冲,夏修身.铁路空心高墩的地震反应分析[J].兰州交通大学学报,2005,24(4):20-23.

[7]尹之潜,李树桢,杨淑文.高层建筑的P-Δ效应和变形计算方法[J].地震工程与工程振动,1992,12(3):71-76.