真实表面色色域三维分析及其色立体计算
李 彦,王 静,李桂苓
(1.天津师范大学 物理与电子信息学院,天津 300387;2.天津大学 电子信息工程学院,天津 300072)
电视系统和显示器的色域宽窄决定了系统传输和显示器重显的颜色范围,拟传输和重显自然界、人工合成的丰富颜色,系统和显示器需有足够宽的色域[1]。
科技界对色域的研究,经历了从不均匀色空间到均匀色空间、从二维到三维色空间的演变[2]。为与主观感受接近,评价电视系统和显示器色域大小应在均匀色空间u'v'坐标系进行。传统方法是在二维色图度上,比较红(R)、绿(G)和蓝(B)三基色三角形与可见光谱色轨迹内的面积,定义二者的比值为色域覆盖率。
因二维色域研究未着眼于亮度信息,故有一定局限性。为此,本文首先在三维CIE-L*a*b*色空间对真实表面色色域进行了模拟,直观地给出了色域在亮度、色调和饱和度方面的三维分布,接着提出并实验了一种精度较高的色域体积算法,可用于三维色域定量评价。
1 真实表面色色域三维分析
真实表面色色域即Pointer色域[3]。M.R.Pointer早年广泛采集、测试和分析了4089种颜色样品或样品数据,并从它们组成的色立体表面选出576种色样构成Pointer色域。该色域包含自然界和人工合成的大部分颜色,其表面的576种颜色为该色域对应于不同色调和亮度(明度)的饱和色,称为真实表面色。Pointer色域宽于现行电视系统的常规色域,被ITU-R BT.1361建议书选定为宽色域电视系统的目标色域。
Pointer将576种真实表面色划分为16个明度和36种色调,并给出其色度参数。由于Pointer色域具代表性,所以本文的分析和计算基于这些数据进行。为简化计算,本文从这些数据中,选用了亮度从20到90,以10为间隔的8个等灰度面,其边界按色调角从0°~360°,以10°为步长的36种色调,共288种颜色的色度数据。
在L*a*b*色空间研究Pointer色域可在两个坐标系进行:1)直接在L*a*b*坐标系;2)将L*a*b*坐标系变换到L*C*hab坐标系,变换如式(1)、式(2)所示

式中:C*表示色彩度(与饱和度相联系);hab为色调角。
在L*a*b*色空间,按8个等亮度面画出的Pointer色域三维分布如图1所示,8个等亮度面的二维表示见图2。图1中,纵坐标轴L*对应黑—灰—白中性色,自下向上亮度逐渐提高。以纵坐标轴为轴,以a*坐标轴正向为0°,逆时针旋转一周,对应色调由红色到品色的色调变化。按照文献[4],将L*a*b*空色间划分成6个色调区,分别是:红(10°~58°)、黄(58°~120°)、绿(120°~220°)、青(220°~270°)、蓝(270°~320°)和品(320°~10°)。
同一色调的颜色,由色域表面到纵坐标轴,色饱和度逐渐降低,色域表面对应电视系统的饱和色。沿纵坐标轴自下至上,色明度逐级提高。图1和图2表明Pointer色域呈上下窄、中间宽的特点,等亮度面由低到高向b*坐标轴的正向偏斜,表面不规则。

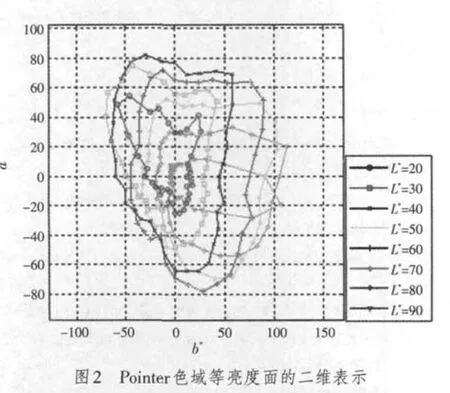
Pointer色域中,任一颜色点到纵坐标轴的距离称彩度半径。表1开列了在6个色调区域内找到的不同亮度(L*)平面上的最大彩度半径C*。

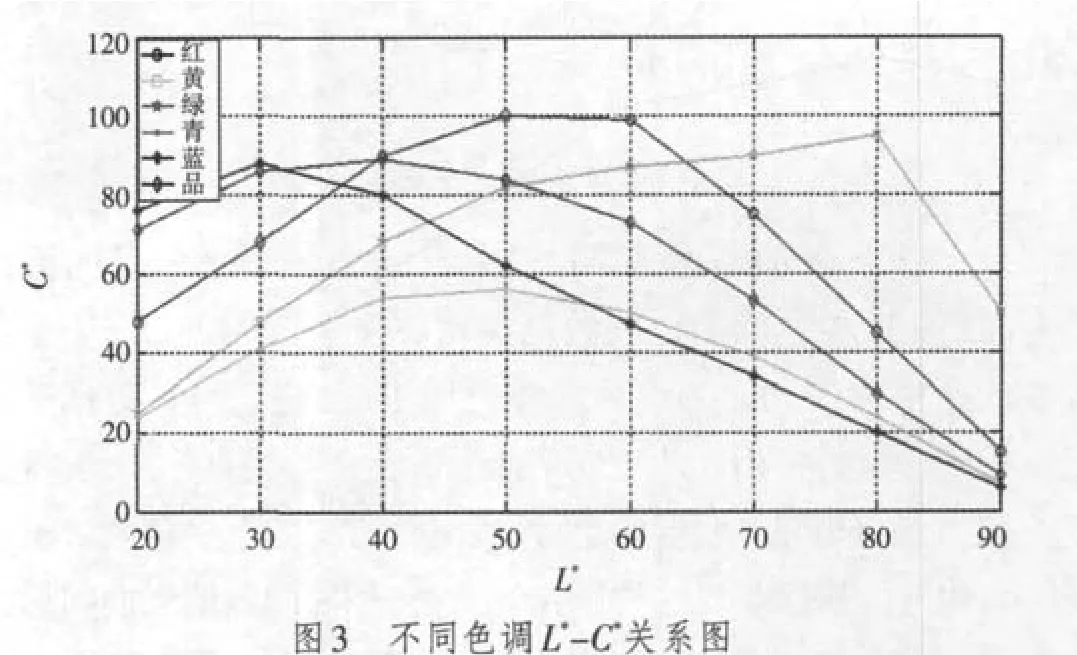
表1 不同色调区域内各亮度平面上的最大彩度半径
以色调分区为参变量,按表1数据绘制的L*-C*线图见图3。图3展现了6个不同色调区域内最大彩度半径随亮度的变化。可知,黄色和绿色主要分布在高亮度区,而蓝色和品色主要分布在低亮度区。这意味着自然界和人工合成的黄色和绿色亮度较高。对显示器来讲,绿色和黄色对亮度贡献较大,改善绿基色发光效率,增设黄元色,可提高显示器重显图像的亮度,有利节能。目前市场上的四元色液晶显示器即在红、绿、蓝三基色的基础上,增设了黄元色。
按表1数据绘制的C*-hab线图见图4。该图选20,50,90三个等亮度面,显示出了最大彩度半径C*与色调角hab的关系。该图表明,低亮度对蓝色表现力较好,而高亮度利于表现黄色。

2 真实表面色色域体积计算
如上文所述,对不同亮度,Pointer色域的大小、形状和在色空间中的位置均不同。这表明,在二维色度图上评价色域大小并不全面,而应在三维色空间,用色域体积表征。例如在图1中,对应立方体体积大的色调区,相应色调的颜色数量多、范围广。
图1、图2表明,Pointer色域边形极不规整,精确计算其体积十分困难,而实用中从数量不多的实测数据计算会更加不准确。为此,本文提出一种棱锥分割法,如图5所示。

以下在L*a*b*色空间,选Pointer色域的8个等明度面,各36种色调的色度数据说明算法。首先,取L*a*b*坐标系中的(0,0,50)点为三维色域中心,将其与各数据点相连;其次,将相邻两亮度平面上等色调数据点相连;再将数据点与相邻等明度面上,按顺时针方向的下一色调数据点相连。依次重复这种操作。最终,相邻两等明度面间形成72个小三角形平面,它们与色域中心相连,形成72个小三棱锥体。三维色域总体积即上下两多边形平面与中心相连的多棱锥体积与8个等亮度面所夹504个三棱锥体积之和。上下底面与中心点连成的多棱锥体积(Vtb)

式中:St,ht分别为L*=90的亮度平面面积及其距中心点的距离;Sb,hb分别为L*=20亮度平面面积及其距中心点的距离。
若已知小三棱锥顶点坐标分别为(a1,b1,L1),(a2,b2,L2),(a3,b3,L3),(a4,b4,L4),则其体积(Vc)为

于是Pointer色域体积(Vp)为

若需更精确结果,可选Pointer色域全部数据,或增加实测数据,或进一步插值,来减小以三角形平面替代色域曲面的误差,再进行如上计算。
3 真实表面色色域体积算法比较
下文将本文算法与笔者早期在文献[5]中提出的棱台算法进行比较。表2列出了两种算法对Pointer色域的计算结果。

表2 三棱锥分割法与棱台法比较
两种方法都是把色域边界邻近数据点近似成平面再计算体积,均会带来误差。两者的差别在于:棱台法将上下两相邻等亮度面与两相邻等色调边界相交的四个点近似成平面;三棱锥分割法把相邻等亮度面上相邻三个数据点近似成平面,再进行体积分割,因此误差相对较小。
4 结束语
Pointer色域涵盖了自然界和人工合成色彩,且被ITU选定为宽色域电视系统的目标色域,对其进行全面分析十分必要。
本文首先将其在L*a*b*色空间和L*C*hab坐标系,进行了三维色度学分析,指出其色域分布随亮度变化,形状、大小和位置均不同,这可为扩展电视系统色域,提高显示器亮度等提供依据。
本文还提出用三棱锥分割法计算Pointer色域体积,并将计算结果与棱台法进行了比较,表明精度有所提高。这为把色域评价由二维色度图提升到三维色空间打下了基础。
[1]胡威捷,汤顺青,朱正芳.现代颜色技术原理与应用[M].北京:北京理工大学出版社,2007.
[2]王凯,吕毅军,高玉林,等.LCD显示器三维色域测量和不同色空间的应用对比[J].光电技术应用,2011,25(6):18-22.
[3]POINTER M R.The gamut of real surface colours[J].Color Research and Application,1980,5(3):145-155.
[4]徐艳芳,黄敏,刘浩学,等.基于色调区域分割的扫描仪颜色转换[C]//2006《数字成像技术及影像材料科学》学术交流论文集.北京:中国科协年会,2006:159-163.
[5]李彦.高清晰度电视系统三维色域研究[J].南开大学学报:自然科学版,2011,44(1):30-35.

