分流墙的设置对疏散效率和安全性影响的研究
□王金晶 郑小平 王亚飞 程 远 [北京化工大学 北京 100029]
引言
分流墙常常设置在剧院、电影院等公共场所出口处,对外部环境起到遮挡作用。然而,在紧急情况下分流墙对人群疏散有着直接影响,分流墙的长度及其与出口的距离都是影响人群疏散效率及其安全性的重要因素。
目前对分流墙的相关研究较少,部分学者对出口前设置小型圆柱的问题予以关注。Helbing和Kirchner等人使用社会力模型和CA模型发现在紧急情形下通过在出口附近设置一个圆柱可以缓解逃生者在逃出房间时可能形成的致命挤压力,提高疏散效率[1,2]。Helbing也提到传统的方式规划行人设施不能保证避开堵塞等情形,特别是在紧急情形下[3]。而圆柱能够降低拥挤人群的挤压力,如果放置的位置和设计的合理还能够提高疏散的有效性和安全性。其他学者Yanagisawa.和 Tanimoto等也发现设置类似圆柱的小型设施可以减少出口前的冲突,从而提高了疏散效率[4,5]。Daichi Yanagisawa等人引入冲突函数来进一步说明小型圆柱是占据了冲突中人的位置,使得参与冲突的人数下降,从而提高流率[6]。在这篇文章的基础上,Daichi等人引入转移角度函数来说明小型圆柱的位置会使得逃生者向出口移动的角度发生改变[7]。分流墙的功能与小型圆柱类似,并且分流效果更加明显。Kirchner等人发现出口前设置分流墙可以改变地板场值,进而改变逃生者的逃生路径,以此可以明显改变疏散效率[8]。Zheng等人发现改变分流墙的长度不但会影响到疏散时间,而且会影响到局部人群拥挤程度[9]。Frank与Dorso分析比较了分流墙到出口的距离对有躲避策略和无躲避策略的两类人群的疏散效率的影响[10]。关于分流墙的长度和位置对紧急疏散的共同影响,目前尚不清楚,需要全面的研究。
本文针对分流墙的长度和位置对人群疏散的影响规律的问题,基于CA建立了地板场模型并进行赋值,经过大量的仿真实验,从结果中提取分流墙设置的相关参数,进而对分流墙的合理设置提供理论依据。
一、模型方法
本文选定的场景为出口前设置一个分流墙的封闭空间,将其划分为二维元胞的结构,设定每个元胞的大小为0.4*0.4 ;同时假设逃生者的平均速率为1m/s,一个时间步长为0.4s。研究中应用地板场模型[11,12]以及出口选择模型进行人群动力学模拟。
(一)静态地板场
本文借鉴Varas 等的静态场赋值方法[12]。设分流墙位置赋予无穷值,出口位置为0,从出口处依次往下计算,遍历当前元胞的摩尔邻域,相应元胞的地板场值加1,对角线方向加。得到的地板场记为地板场0,具体赋值见图1(a)。在紧急疏散过程中,人群将由高场值区域向低场值区域移动(如图1(b))。对于每一个逃生者,向一个空的邻域元胞移动的转移概率Pij为:

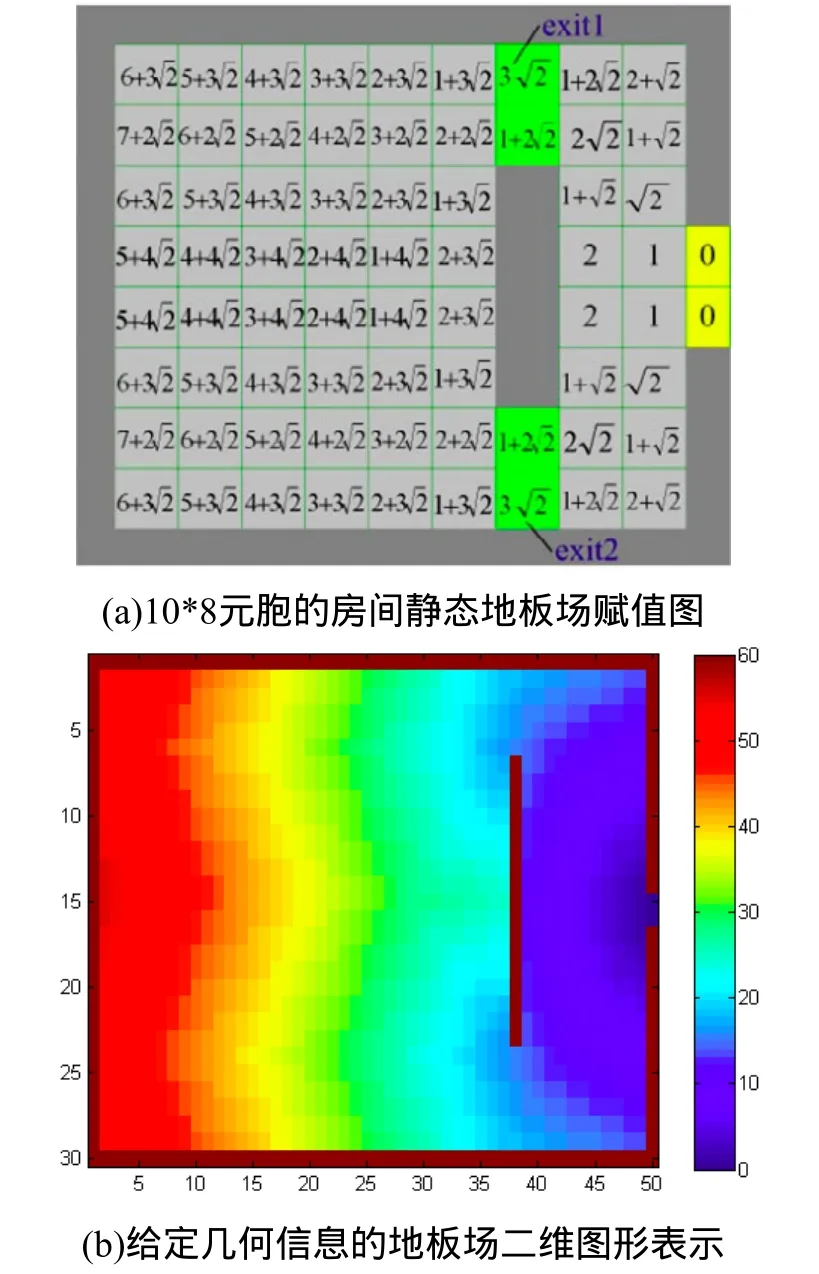
图1
(二)出口选择
分流墙的两端可以视为两个分出口(如图1(a)),因此应用logit-based离散选择准则来获得逃生者的出口选择概率。首先用Zheng等人中提到的方法来标定地板场1和地板场2,当处于位置x的逃生者选定其中一个出口后,则可通过相应的地板场更新位置[9]。然而,由于疏散过程是动态的以至于逃生者可能会根据环境的变化更换出口[13]。
因为逃生的距离以及排队等待的时间决定疏散时间,所以考虑如下两个因素:(1)从当前位置到出口的移动距离(X),(2)在出口处每单位的出口等待人数(X)。(X)可根据下式计算
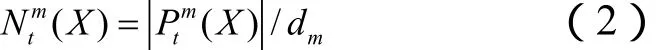
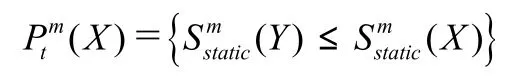
因此,根据logit模型,可以得到选择出口的概率公式为
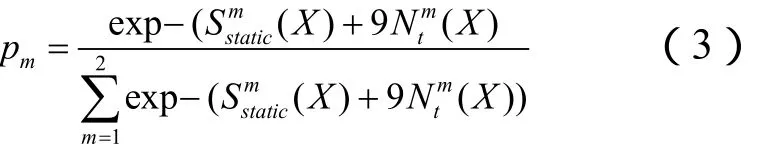
(三)冲突的解决
如图2所示,由于采用同步更新机制可能会有冲突现象发生,这时逃生者可能会停滞。引用Tanimoto等人中的停滞概率函数μ(K),当k个人竞争同一格子时,以1-μ(K)的概率随机选择冲突中的一个人移动,而其他人则停留在原地[4]。根据对冲突函数的定义,可知冲突是作用于逃生者之间的某种局部压力。ξ∈[0,1]为争抢系数,表示当遇到冲突时不愿意谦让的概率。ξ越大,逃生者进入期望元胞的欲望越强,拥挤程度增强,逃生者之间的相互作用也就越强。这种局部效应对宏观量疏散时间和流率具有相当大的影响。当ξ=0时,所有人都谦让别人避开了冲突的情形,也就是经常看到的排队行为。ξ>0.5,表示竞争行为,随着ξ的增加,竞争程度增大。ξ>0.5,表示轻竞争行为,当遇到冲突时,逃生者首先表现出的是竞争,但是会想到谦让。ξ<0.8,表示重竞争行为,即Helbing 等人在社会力模型中提到的恐慌行为[1]。冲突数量急剧上升,外出流被抑制,逃生者之间的挤压力如此强烈以至于移动很困难。直到ξ=1时,完全竞争状态,没有人进入目标元胞。
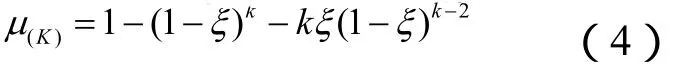
模拟过程如下:
Step 1: 计算每个逃生者的转移概率(公式(1))和地板场0、地板场1和2。
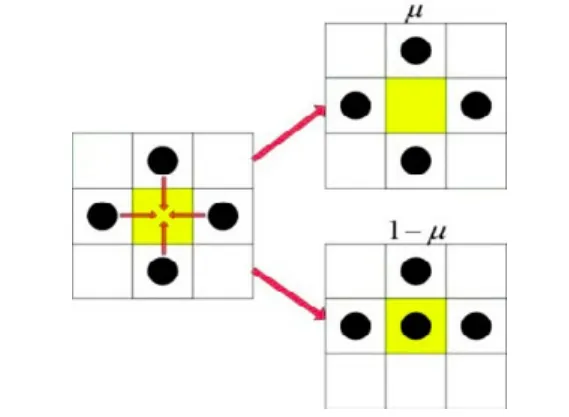
图2 冲突的解决
Step 2: 判断逃生者的位置:如果在分流墙左边根据2节中提到的出口选择概率公式动态选择出口,基于地板场1或2更新自己的位置;若在分流墙与出口之间,将基于地板场0更新位置。
Step 3: 逃生者基于转移概率公式移动一个元胞。如果移动时遇到冲突,用上文中提到的方法解决。
Step 4: 处于出口位置(如图1(a))的逃生者将会从疏散场景中移除。
二、模拟结果及讨论
疏散场景假定为M*N元胞的空间,逃生者最初随机分布在一个特定的范围。仿真中出现的参数包括ρ,l, d,w。其中是ρ逃生者的人群密度,l为分流墙的长度,d为分流墙到出口的距离,w为出口的宽度。设分流墙的设置使两个分出口的宽度相同,否则每个出口会因为使用效率的不同延长疏散时间,并引起 Zhao等人提到的疏散的不平衡的现象[14]。另外,考虑到随机因素,每一个数据都是 100次模拟的平均值。
(一)出口选择参数的确定
设场景内部空间为 48*38,w=2,d=3,l=12,ξ=0.7,ρ=0.1,逃生者最初随机分布在房间左上角的20*20个元胞内,如3所示。
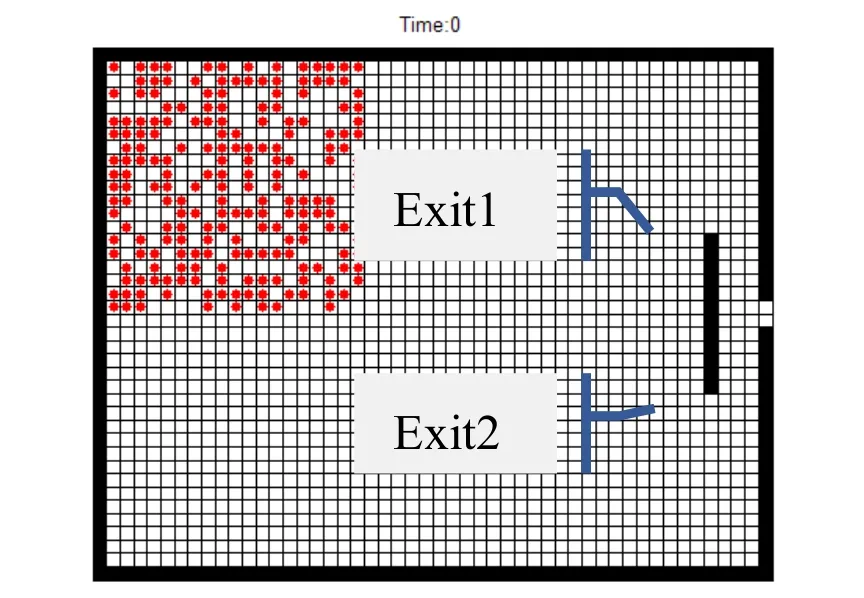
图3 逃生者初始密度ρ=0.1,随机分布在房间左上角的20*20个元胞内


图4 当人群避开系数θ从1到20变化:(a)分流墙两边分出口前的人群分布图(总的逃生者人数为200,红色表示Exit1前的人逃生者人数,蓝色表示Exit2前的逃生者人数);(b)逃生者逃出房间的总疏散时间
图4(a)所示,当θ=0时,由于逃生者只考虑到出口的最短距离,因此都向靠近初始位置的exit1移动,导致exit2前无人群分布,出口的使用效率下降。当θ<5时,只有小部分人向人少的exit2移动。随着θ的增大,越来越多的逃生者考虑到了出口前人群分布的因素,exit2前的人数逐渐增多。当θ>10之后,可以看到分流墙两边的逃生者人数趋于相等,两个出口都得到了合理利用。观察图 4(b),可以发现随着人群避开系数θ的增加,疏散时间逐渐下降,说明出口得到了有效的利用可以使得疏散效率提高。直到θ>10之后,疏散时间趋于平稳。
通过上面的分析,得到θ=10是一个较理想的值。逃生者可以综合考虑最短路径及出口前的人群分布合理选择出口。因此,在下面的仿真中,取θ=10作为人群避开系数。
(二)分流墙的设置
出口前的分流墙改变了逃生者的行走路径,其分流作用会影响到疏散的安全性和有效性。在以下的仿真试验中,考虑疏散过程中的冲突次数和人群流率两个方面,得到最优的分流墙设置。
1.分流墙对冲突次数的影响
设场景内部空间的元胞分布为48*38,ρ=0.15,w=2,ξ=0.8。图5的颜色图表示在疏散过程中各点发生冲突的次数。
图5所示,出口前无分流墙和有分流墙时,冲突的分布差异很大。图 5(a)中,出口前无分流墙,冲突主要发生在出口前;图 5(b)中,出口前的分流墙使得人群分流,分流墙两端的冲突次数增加,尤其是分出口前的一个位置(图5(b)所示),而最终出口前的冲突次数由328次下降到220次。因此,分流墙起到降低出口前冲突的作用,下面具体研究分流墙的设置对于冲突分布的影响。
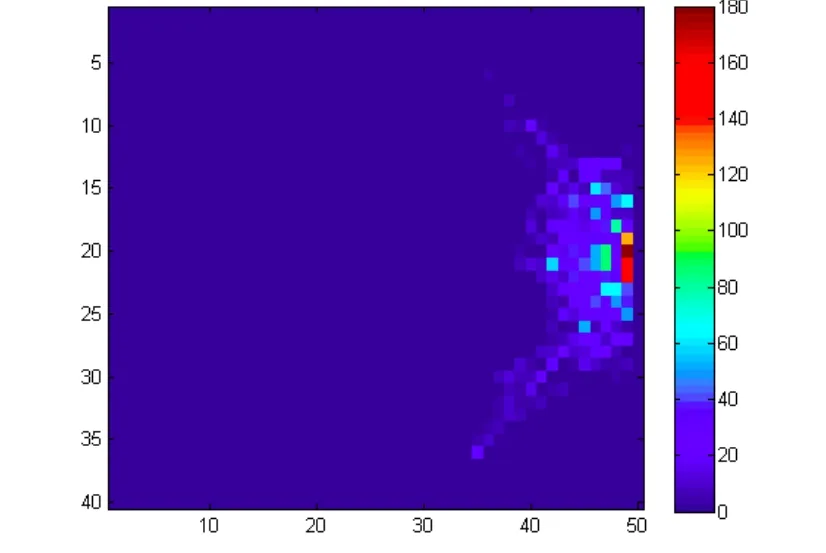
图5 (a)没有分流墙时,出口前的冲突分布

图5 (b)l=12,d=3时,出口前的冲突分布

图6 冲突发生的次数随争抢系数的变化关系(a)ξ=0.7(b)ξ=0.3
内部空间元胞尺寸为38*28,ρ=0.25,w=2,(a)ξ=0.7;(b)ξ=0.3。长度l从2到26、d从1到4变化,疏散过程中的冲突发生的总次数如图6所示。
当ξ=0.7,d=2使得冲突次数最多,d=3使得冲突次数最少;ξ=0.3,d=4使得冲突次数最多,d=1使得冲突次数最少。而当争抢系数不同时,l=14时冲突的次数最少。使得冲突次数最少的长度取值都为疏散空间宽度的1/2,说明使得冲突次数最少的长度最优值与争抢系数、分流墙到出口的距离无关。
研究争抢系数对冲突次数的影响。设疏散空间内部的元胞分布为38*28,w=2,ρ=0.25,l=14,争抢系数从0~0.9变化。d取不同值时,疏散过程中发生的冲突次数如图7所示。
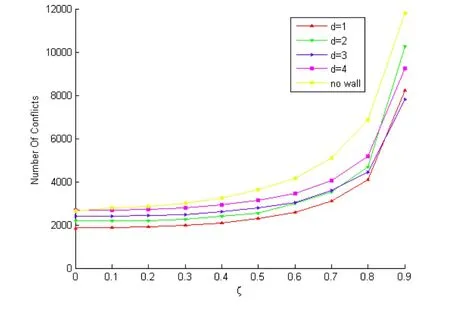
图7 冲突次数随争抢系数ξ的变化图
图7所示,ξ值从0~0.9变化过程中,无分流墙时的冲突次数最多。随着争抢系数的增加,冲突的数量将有不同幅度的上升,尤其是无分流墙的情形。即疏散刚开始一段时间,所有的逃生者都在出口前形成一个大的拥挤。从图中可以看到,当ξ<0.5时,分流墙到出口的距离越远,冲突发生的次数越多。当ξ≥0.5之后,d=2的疏散时间上升幅度较大。说明分流墙到出口的距离为2时,疏散的安全性最弱。在ξ<0.9时,d=1的情况下冲突次数最少。而当ξ=0.9时,d=3使得冲突发生的次数最少即疏散安全性最高。
综合上面的仿真实验,得到结论:设置分流墙能够明显地减轻疏散过程中的冲突程度,提高疏散的安全性。使得冲突次数最少的分流墙的设置:ξ<0.9时,d=1;当ξ=0.9时,d=3。分流墙的长度为疏散空间宽度的1/2。
2.分流墙对疏散效率的影响
Case1:场景内部空间元胞分布为38*28个元胞,逃生者人群密度始终保持ρ=0.38不变,争抢系数ξ=0.8。当出口宽度分别为w=2;w=4;w=6时,l从2~6、d从1~4变化时,出口的流率变化的曲线如图8所示。
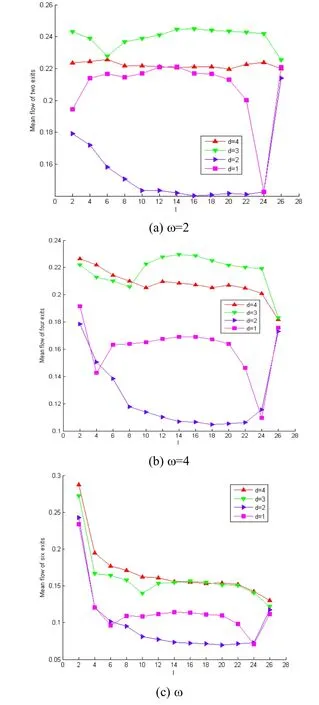
图8 不同的出口宽度下,出口的平均流率(l从2~6变化,d从1~4变化)
图8所示,分流墙的长度和位置变化对疏散效率的影响很明显。w=2和w=4(图8a-b),d=3的情况下出口流率最高。当w=6时(图8c),随着分流墙长度的增加,平均流率一直下降,说明设置分流墙不但没有提高疏散效率,反而阻碍了疏散。
因此,当分流墙存在时,出口的宽度存在某一个临界值,在临界值之上设置分流墙将失去它的作用。这个结论与Zhao等人得到的结论相同[15]。使得疏散效率最高的分流墙的设置为:d=3,l=14(疏散场景宽度的1/2)。
Case2:设场景内部空间元胞分布为48*48元胞,w=2,ρ=0.17不变。当ξ=0.9,ξ=0.6时,l从 2~48、d从1~4变化时,出口流率变化的曲线如图9。

图9 不同的争抢参数下(a)ξ=0.9(b)ξ=0.6,出口的平均流率(l从2~48变化、d从1~4变化)
图9所示,当ξ=0.6时,使得出口流率达到最高的分流墙的设置为d=1,l=24;当ξ=0.9时,d=3,l=24。因此,当争抢参数不同时,使得疏散效率达到最高的l取值为24(疏散空间宽度的1/2),与争抢系数无关;而d的取值与ξ有关,下面将具体研究它们之间的关系。
图10所示,在ξ值较小时,分流墙的位置对出口流率几乎没有影响。这说明疏散者不存在冲突时,分流墙的位置对疏散效率是没有影响的。但是,随着ξ的增加,分流墙对疏散过程的影响效果越明显。当 ξ>0.5时,即疏散者表现出竞争行为时,分流墙的合理位置使得疏散时间开始下降。几乎所有的冲突都是发生在出口前,它们对外出流有直接的影响,导致流率下降。而合理的分流墙的位置使得人群分流,冲突的位置主要发生在分流墙两侧。分流墙抑制了出口前的堵塞从而使得外出流提高。但是随着ξ的变化,分流墙的位置使得出口流率最高的取值是不同的:当 0.8≥ξ>0.5时,d=1;当 ξ>0.8之后,d=3。当分流墙到出口的距离为1时,冲突主要发生在分流墙的两侧,最终出口前几乎没有冲突,所以会使得疏散效率大大提高。但是当疏散者处于高度的竞争状态中,疏散者之间一旦发生冲突,都将很难移动。而分流墙到出口之间只能容纳一个人,这个位置还是冲突发生较频繁的位置。当争抢系数足够大时,每一时步有很小的概率通过分流墙向出口移动,导致疏散效率下降。而当d=3时,即使分流墙两端的冲突严重,但是由于分流墙到出口这个范围较宽广,还会有疏散者通过分流墙向出口移动。
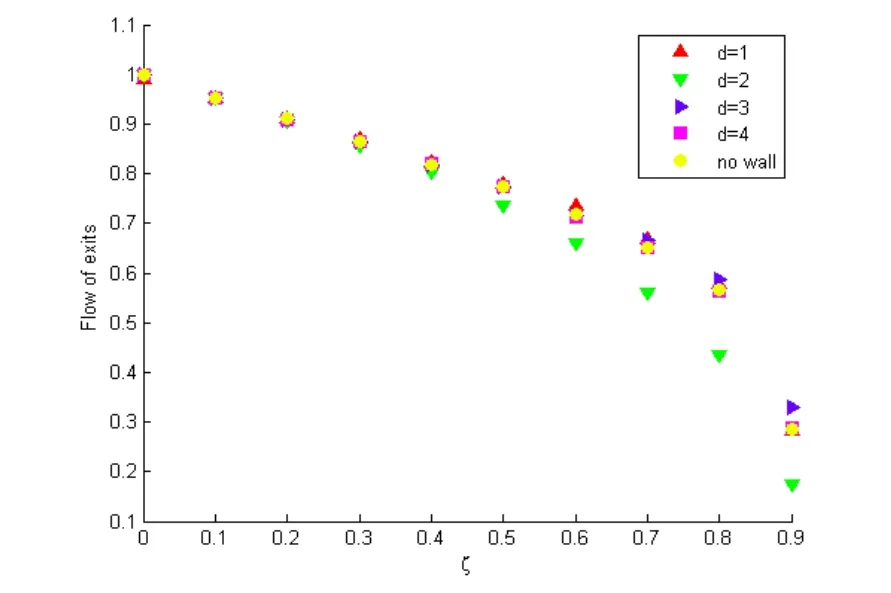
图10 出口流率随争抢系数ξ的变化图
综合上面的仿真实验,得出结论:依据实际情况合理设置分流墙能够提高疏散效率。使得流率最高的分流墙的设置:当ξ>0.8,即在紧急疏散中逃生者都处于高度的竞争状态,d=3时疏散效率最高。当0.8≥ξ>0.5,d=1时疏散效率最高。
三、结论
本文基于 CA模型对存在分流墙的单出口空间进行了地板场赋值,并引入了出口选择模型和冲突函数来表现分流墙的作用。出口选择参数可以调节分流墙两端出口前的人群密度,合适的出口选择参数可以能够使得分流墙两端的分出口得到合理的利用,提高疏散效率。冲突函数的引入对重现分流墙缓解人群内部压力的作用是很有必要的。ξ>0.5,表示竞争行为,随着ξ的增加,竞争程度增大。
在疏散过程中,分流墙能够降低冲突的次数,提高疏散的安全性;而逃生者在竞争行为下,设置分流墙对提高疏散效率有一定的意义。基于疏散的安全性和有效性,综合考虑疏散过程中的冲突次数及出口流率,经过分析讨论得到分流墙的最优设置。
1.当遇到冲突时,逃生者表现出重竞争行为时,分流墙到出口的距离为3个元胞时,效率最高;而表现出轻竞争行为时,分流墙到出口的距离为1个元胞时,疏散效率最高。
2.分流墙的长度设置为疏散空间宽度的1/2时,疏散过程中的冲突次数最少,即疏散的安全性最高高。长度的最优值与竞争程度、分流墙到出口的距离无关。
[1]HELBING D, FARKAS I, VICSEK T.Simulating dynamical features of escape panic[J].Nature, 2000: 407-487.
[2]KIRCHNER, A NISHINARI K, SCHADSCHNEIDER A.Friction effects and clogging in a cellular automaton model for pedestrian dynamics[J].Physical Review E ,2003, 67:0561221.
[3]HELBING D, BUZNA L, JOHANSSON A ,WERNER T.Self-organized pedestrian crowd dynamics: experiments,simulations, and design solutions[J].Transportation Science,2005, 39: 1-24.
[4]YANAGISAWA D, NISHINARI K.Mean-field theory for pedestrian outflow through an exit[J].Physical Review E,2007, 76: 061117.
[5]TANIMOTO J, HAGISHIMA A, TANAKA Y.Study of bottleneck effect at an emergency evacuation exit using cellular automata model, mean field approximation analysis, and game theorys[J].Physica A: statistical mechanics and its applications,2010, 389(24): 5611-5618.
[6]YANAGISAWA D, TOMOEDA A, NISHINARI K.Conflicts at an Exit in Pedestrian Dynamics[J].Pedestrion and evacuation dynamics 2008, 2010, 2: 491-502.
[7]YANAGISAWA D, KIMURA A, TOMOEDA A, et al.Introduction of Frictional and Turning Function for Pedestrian Outflow with an Obstacle[J].Physical Review E, 2009, 80:036110.
[8]KIRCHNER A, NAMAZI A, SCHADSCHNEIDER A.Extended floor field CA model for evacuation dynamics[J].IEICE TRANSACTIONS on Information and systems , 2004,87(3): 726-732.
[9]ZHENG Xiao-Ping, LI Wei, CHAO Guan.Simulation of evacuation processes in a square with a partition wall using a cellular automaton model for pedestrian dynamics[J].Physica A:statistical mechanics and its applications, 2010, 389(11):2177-2188.
[10]FRANK C A, DORSO C O.Room evacuation in the presence of an obstacle[J].Physical A: statistical mechanics and its applications, 2011, 390(11): 2135-2145.
[11]HUANG Hai-Jun, GUO Ren-Yong.Static floor field and exit choice for pedestrian evacuation in rooms with internal obstacles and multiple exits[J].Physical Review E, 2008, 78:021131.
[12]VARAS A, CORNEJO M D, MAINEMER D, et al.Cellular automaton model for evacuation process with obstacles[J].Physical A: statistical mechanics and its applications, 2007, 382(2): 631-642.
[13]ALIZADEH R.A dynamic cellular automaton model for evacuation process with obstacles[J].Safety Science, 2011,49: 315-323.
[14]ZHAO D L, LI J, ZHU Y, ZOU L.The application of a two-dimensional cellular automata random model to the performance-based design of building exit[J].Building and Environment, 2008, 43(4): 518-522.
[15]ZHAO D L, YANG L Z, LI J.Exit dynamics of occupant evacuation in an emergency[J].Physical A: statistical mechanics and its applications, 2006, 363(2): 501-511.

